一種面向語音識別的抗噪SVM參數優化方法

白靜，楊利紅，張雪英

(太原理工大學 信息工程學院，山西 太原，030024)

語音識別技術是人機接口應用的前沿技術之一，目的是使計算機能夠聽懂人類語言，實現人機語音通信。但目前多數實際語音識別系統只適合識別“干凈”的語音，當存在背景噪聲或訓練和測試環境不同時，系統性能會急劇下降。作為模式識別的新型方法之一，支持向量機(SVM)[1]能較好地解決小樣本、非線性、高維數和局部極小點等實際問題，比基于經驗風險最小化的隱馬爾可夫模型(HMM)[2]、人工神經網絡[3]等方法具有更好的泛化能力和分類精確性[4]，更適合用于語音識別。關于支持向量機的理論研究在逐漸增多，但應用研究相對滯后，只在一些領域得到較好應用，如文本自動分類、圖像識別、視頻編碼[5-6]等，近些年 SVM應用研究開始擴展到語音識別領域，但還很不夠。文獻[7-8]是早期的國內將支持向量機應用于孤立詞和漢語數字語音識別的文獻，取得了與隱馬爾可夫模型相當的識別效果，但采用的是最基本的核函數，核參數選用的是經驗值，并未對 SVM 中的參數選擇進行描述，而且實驗是在非噪音環境下進行的；Liu等[9]將SVM與段長分布HMM融合起來，構造出一種混合系統，將該系統應用到普通話數字語音識別系統中，實驗是在不同信噪比下進行的，結果僅優于使用段長分布HMM的結果。在信噪比較高時，能有效改善系統性能，但在信噪比低于15 dB時，效果不好，且整個系統算法比較復雜。李攀等[10-11]將動態時間規整(DTW)算法嵌入支持向量機常用的核函數中，解決了語音段時長不一致的問題, 實現了支持向量機對語音的分類識別，但這僅是一種進行語音識別的方法，SVM的核參數仍然是最基本的經驗值。Maldonado等[12]在不同信噪比下對西班牙語的孤立數字進行實驗，結果優于使用HMM的結果，但在低信噪比環境下識別率仍不高，未對SVM算法部分進行深入研究。將 SVM 應用于語音識別有著巨大的研究潛力。已有研究表明：SVM核參數及懲罰因子的選擇嚴重影響著其分類性能，當其值選取合適時，SVM的分類能力明顯增強，然而，其參數的選取目前仍沒有較有效的方法。人工魚群算法[13]是一種基于模擬魚群行為的優化算法，其結構簡單、參數調整簡單易行，更適合計算機編程處理。本文在分析SVM模型抗噪性的基礎上，提出一種改進的人工魚群算法——基于小生境共享機制的并行結構人工魚群算法(PAFSA)，對支持向量機中核參數及懲罰因子進行優化，并用基于優選參數的支持向量機進行語音識別實驗。

1 SVM模型的抗噪性分析

根據SVM定義，對于空間Rn上的線性可分的2類分類問題，有最大間隔原則，即最大化相應的2個支持超平面形成的間隔。由該原則出發，設有l個線性可分的訓練樣本集 T={(x1，y1)，(x2，y2)，…，(xl，yl)}∈(X，Y)l，輸入樣本空間 xi∈X=Rn，輸出 yi∈Y，Y=(-1，1)(其中，i=1，…，l)，標明它所對應的樣本向量xi屬于兩類中的哪一類，由這一組樣本可以確定一個分類超平面 w·x+b=0，使得離它最近的每類點與它的距離達到最大值，則所得到的最優化問題為對法向量w和截距b的凸二次規劃問題[14]：

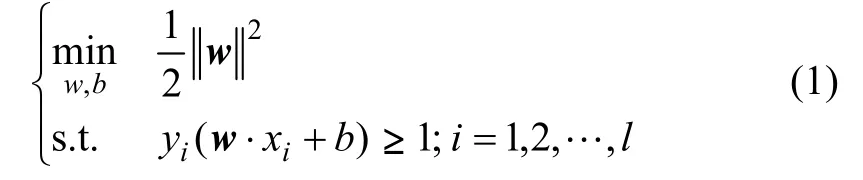
這種解法硬性地要求所有樣本點都滿足和超平面間的距離必須大于 1，因此也叫“硬間隔”分類法。對于某些“離群點”，就無法滿足這個硬性的條件，從而使得整個問題無解。若繼續使用超平面進行分劃，則需引入“容錯性”，“軟化”對分劃超平面的要求，即允許有不滿足約束條件 yi(w·xi+b)≥1的訓練點存在。“軟化”約束條件的方法是給式(1)中1這個硬性閾值加一個松弛變量，ξi≥0(i=1，…，l)，即：

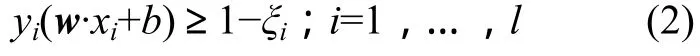
只有“離群點”才有1個松弛變量ξi與其對應，沒離群的點松弛變量都等于 0。松弛變量ξi實際上表示對應點到底離群有多遠，其值越大，則點就越遠。當ξi充分大時，訓練點總可以滿足上述約束條件。但應該設法避免ξi取太大，因此，在目標函數里引入懲罰因子C對其進行懲罰，體現重視離群點帶來損失的程度。這樣，上述原始最優化問題變為：

正因為有了最大間隔原則、松弛變量、懲罰因子，才使得支持向量機具有魯棒性。在對支持向量機魯棒性正確分析的基礎上，當信噪比降低時，語音識別系統抗噪性的研究就是可行的。

2 SVM模型選擇

SVM中的非線性分類問題是通過核函數解決的，通過引入核函數技術把低維空間的輸入數據通過非線性變換映射到高維特征空間，從而在低維空間的非線性問題可以在高維空間用線性方法來解決，并且不用知道非線性變換以及其對應特征空間的形式。SVM由核函數和訓練集完全刻畫，SVM分類性能、核函數的選擇以及核參數的取值起著非常關鍵的作用。

采用不同的核函數可以構造不同的支持向量算法。在實際應用中，通常要根據問題的具體情況選擇合適的核函數及其參數。高斯核具有較好的適應性，無論是低維、高維、小樣本和大樣本等情況均適用，是較理想的分類依據函數。因此，本文采用高斯函數作為核函數，其表達式為

引入核函數K(xi，xj)后，使用Lagrange乘子法可將式(3)的最優化問題轉化為一個二次規劃問題：

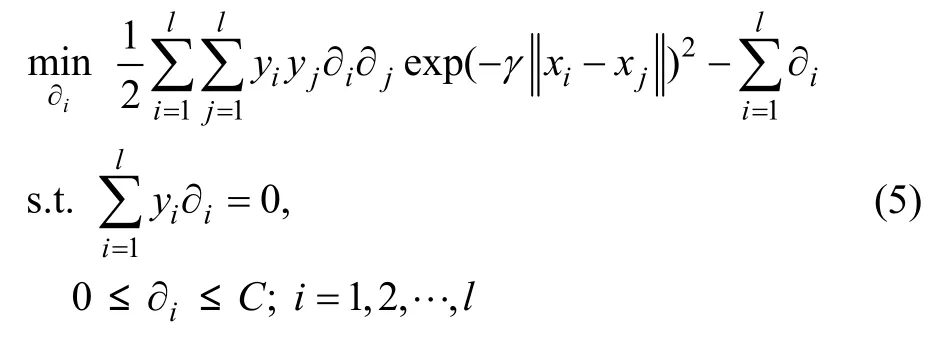
其中：?i為與第i個樣本對應的Lagrange乘子，實質上是凸優化問題的解，?i不為零對應的樣本點xi就是支持向量。對式(5)求解后，得到相應的決策函數：

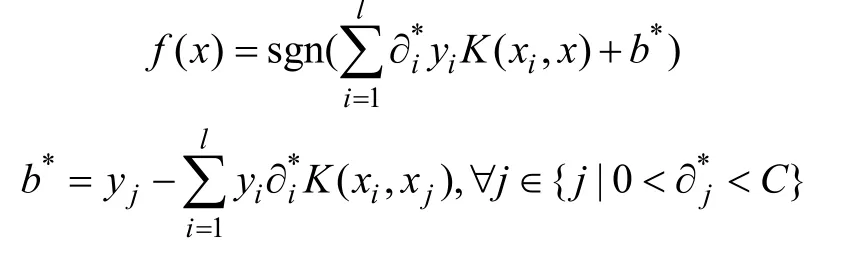
由式(5)可知：SVM分類性能的優劣取決于參數C和γ最小值的求解。核參數γ主要影響樣本數據在高維特征空間中分布的復雜程度，但因為具體學習對象的不同，特征相差較大且沒有固定的規律，目前參數選擇還沒有形成統一的模式[15-16]，因此，本文提出一種基于小生境共享機制的并行人工魚群算法 PAFSA來優化C與γ。并將優選的參數用于語音識別系統。

3 小生境共享機制并行結構人工魚群算法的提出

3.1 基于小生境共享機制的并行人工魚群算法思想

人工魚群算法是應用動物自治體模型提出的一種自下而上的尋優策略，該算法利用魚群的覓食、聚群和追尾行為，從構造單條魚的底層行為做起，通過魚群中個體的局部尋優，達到全局最優值在群體中凸顯的目的。人工魚群算法具有較強的克服局部極值、取得全局極值的能力，并且算法中只使用目標函數值，無需目標函數的梯度等特殊信息，對搜索空間具有一定的自適應能力。

人工魚群算法的出現為解決尋優問題提供新的具有競爭力的求解算法，但是其強大的全局搜索能力可能會使之漏掉最優個體而且搜索的隨機性，也使得求解精度不高。針對這一問題，本文將基于共享機制的小生境技術[17]引入人工魚群算法，小生境技術可以維持樣本個體的多樣性從而避免最優個體的流失。具體算法是將每1代個體劃分為若干類，每個類中選出若干適應度較大的個體作為1個類的優秀代表組成1個群，再在種群中以及不同種群中之間雜交、變異產生新一代個體群，同時選擇分享機制完成任務。基于這種小生境的人工魚群算法可以更好的保持個體的多樣性，同時具有很強的全局尋優能力。

由于基本人工魚群算法的主體循環中僅選擇追尾、聚群和覓食3種行為中的1種執行，這使得優化結果停滯不前或者錯過較優解的概率增大，優化結果不理想。本文對魚群算法在循環主體處進行改進，提出一種并行人工魚群算法，進一步降低錯過較優解的概率。在初始化后直接分2條路徑執行：一條路徑執行追尾行為，其中覓食行為設置為隨機行為；另一條路徑執行聚群行為，同樣設置覓食行為為隨機行為。最后比較兩者的適應值，取最優的結果，記錄于公告板，同時更新個體，繼續迭代尋優。圖1所示為小生境并行人工魚群算法PAFSA的流程圖。

引入小生境共享機制的基本思想是：通過反映個體之間相似程度的共享函數來調節群體中各個個體的適應度，使得在這之后的群體進化過程中，算法能夠依據這個調整后的新適應度來進行選擇運算，以維持群體的多樣性，創造出小生境的進化環境。共享函數是表示群體中2個個體之間密切關系程度的1個函數，表示個體i和j之間的關系，可記為s(i, j)。共享度是某個個體在群體中共享程度的一種度量，它定義為該個體與群體內其它各個個體之間的共享函數值之和，用S表示：

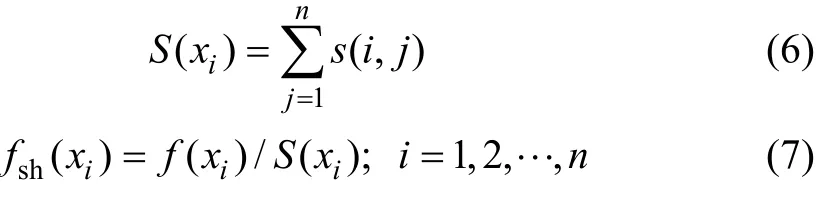
其中：xi為樣本當前狀態；fsh(xi)為xi的共享適應度；f(xi)為 xi的適應度；n為種群個數。依據式(6)和式(7)調整各個個體的適應度，由于每個個體的更新比例是由其適應度來控制的，所以，這種調整適應度的方法就能夠限制群體中個別個體大量增加，從而維護群體的多樣性，并造就一種小生境的進化環境，防止流失最優個體的情況。

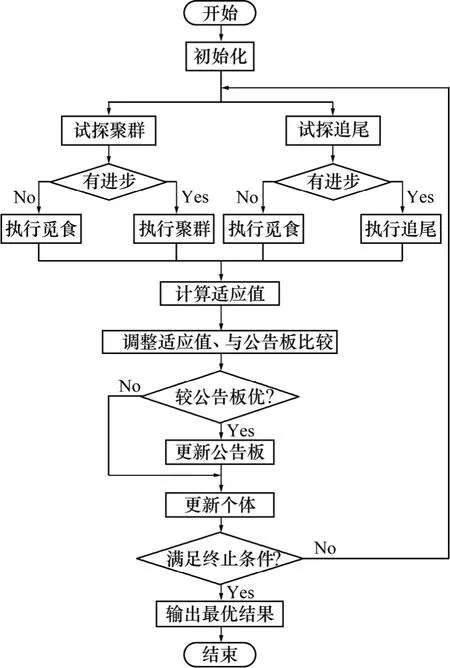
圖1 小生境并行人工魚群算法PAFSA流程圖Fig.1 Flow diagram of PAFSA based on niche sharing mechanism

3.2 PAFSA的算法測試

為檢驗PAFSA算法的性能，選取以下2個典型的測試函數進行算法性能測試。

測試函數1：Goldstein-Price(GP)函數(n=2)。

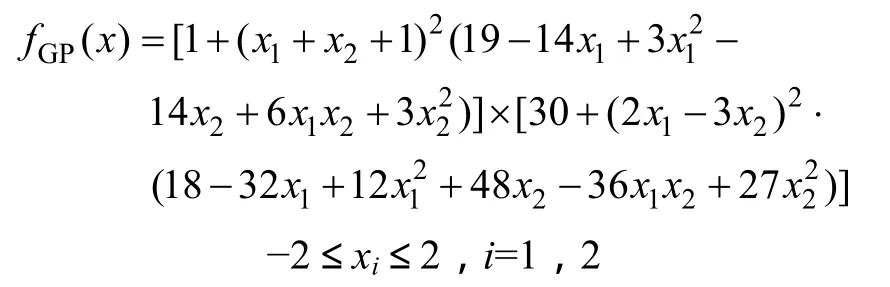
該函數在定義域范圍內的全局最小值為 3，最優點為(0，-1)。其三維函數圖像如圖2所示。

測試函數2：Rastrigin(RA)函數(n=2)。

該函數的表達式包含多項式及典型三角函數，其在定義域范圍內的全局最小值為-2，最優點為(0，0)。其三維函數圖像如圖3所示。

實驗中引入基本粒子群優化算法 PSO，將基本AFSA與PAFSA 2個算法的結果進行比較。均選取函數GP和函數RA作為測試函數，通過進行30次獨立運行得到平均最小函數值和最小值，實驗結果如表 1所示。

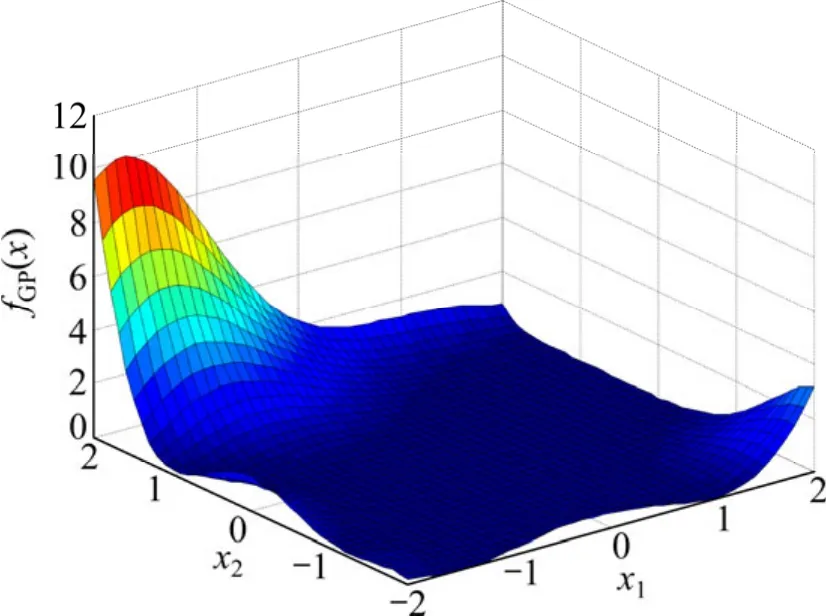
圖2 Goldstein-Price(GP)函數圖像Fig.2 Image of Goldstein-Price (GP) function

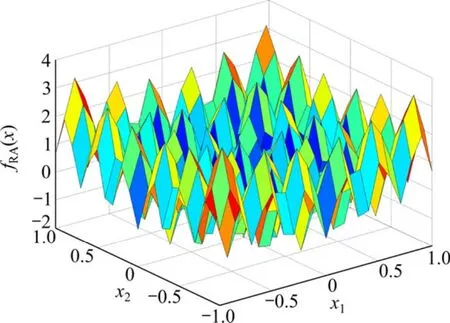
圖3 Rastrigin(RA)函數圖像Fig.3 Image of Rastrigin (RA) function

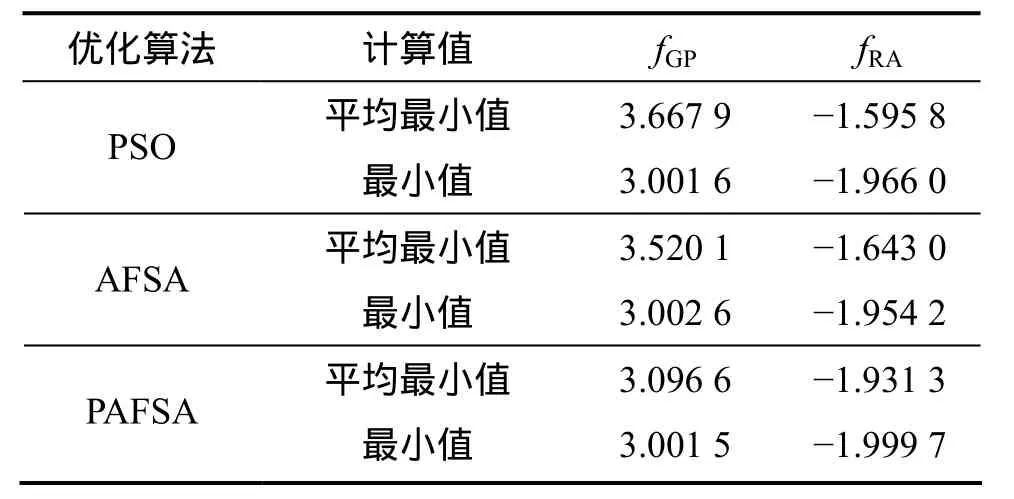
表1 PAFSA與PSO和AFSA算法優化結果比較Table 1 Comparison of optimized results of PAFSA, PSO and FASA

表1表明：PAFSA的優化實驗結果比 AFSA和PSO的穩定，平均最小值和獨立運行最小值更接近理論最優值。圖4和圖5所示為上述3種優化算法分別對2個測試函數的1次尋優過程對比截圖，顯示各自的收斂過程。從圖4和圖5可以看出：PAFSA算法在搜索最優解質量方面要優于AFSA和PSO，即PAFSA能在較少的迭代次數下較快地找出全局最優解，具有較好的收斂性。

圖4 對Goldstrein-Price函數的優化過程Fig.4 Goldstrein-Price function optimization processes of PAFSA, PSO and AFSA

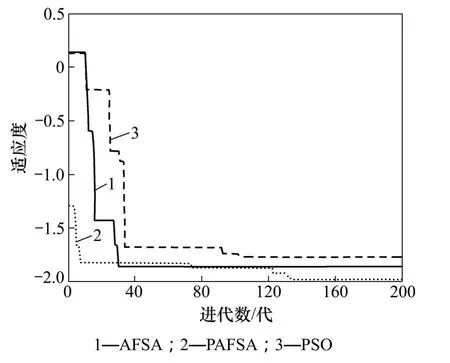
圖5 對Rastrigin函數的優化過程Fig.5 Rastrigin Function optimization processes of PAFSA, PSO and AFSA

3.3 用PAFSA優化SVM參數的實現

將PAFSA產生的初始種群作為SVM參數，代入這些參數進行 SVM 模型訓練和測試。文中將語音詞庫分為2部分并分別作為訓練樣本和測試樣本，試驗后返回一系列訓練樣本識別率。然后，通過聚群、追尾、覓食等行為尋優產生下一代參數種群，再利用新生子群重復上述操作。在達到一定的代數時，對尋優得到的種群進行分析，依據個體的共享度調整對應個體的適應度，再選取最優個體，進行迭代，直到滿足人工魚群算法中設計的終止條件為止，并將得到的最優參數、最優參數模型作為最終預測模型。圖6所示為PAFSA優化SVM參數流程。

圖6 PAFSA優化SVM參數流程圖Fig.6 Flow diagram of SVM parameters optimization by PAFSA

高斯核函數 SVM 的參數優化可看作是尋找合適的誤差懲罰因子C和核參數γ，C與γ構成的二維數組，使 SVM 有較好的分類性能，即讓適應值最大。運用PAFSA在參數C和γ構成的二維平面上尋優，建模的步驟如下。

步驟1：初始化，產生初始種群，確定SVM參數向量(C，γ)的范圍及算法中其他參數值。

步驟2：代入SVM模型，利用初始種群對訓練集進行訓練，由訓練好的模型對測試集進行測試，將總體測試樣本識別率轉換成該模型的適應值。

步驟3：依據適應值，對(C，γ)進行覓食、聚群、追尾等行為進行尋優，產生下一代參數(C，γ)種群。

步驟4：利用得到的子代參數(C，γ)種群，重新對SVM 進行訓練和測試并計算相應的適應值，進行判斷，若達到一定的迭代次數，則依據個體的共享度調整對應個體的適應度，再選取最優個體。

步驟5：運用已得到的子代參數，重新對SVM進行訓練和測試并計算相應的適應值，進行判斷，若滿足人工魚群算法中訓練停止準則，則轉到步驟 5；否則，返回步驟3繼續執行。

步驟6：結束訓練，此時得到的參數(C，γ)為最終模型的參數。

4 實驗結果與分析

實驗中，直接把由采樣系統得到的語音數據文件作為處理對象，所采用的語音樣本為孤立詞。語音信號采樣頻率為11.02 kHz，幀長N為256點，幀移M為128點。

實驗使用9人在不同信噪比(SNR)(0，5，10，15，20，25和30 dB，無噪音)下的發音作為訓練數據庫，噪聲為常見的Gaussian白噪聲，其他噪聲可通過語音識別系統的前端預處理濾波器濾除掉。語音樣本數據的詞匯量分別為10，20，30，40和50個詞，每人每個詞發音3次，因此，整個數據集在不同SNR下分別有10，20，30，40和50個類別，對應的訓練樣本分別有270，540，810，1 080和1 350個。測試樣本由另外7人在相應的SNR和詞匯量下，對每個詞發音3次得到，對應的測試樣本分別有210，420，630，840和1 050個。

實驗輸入的語音特征為改進的 MFCC特征參數(MFDWCs)[18]，該特征的提取符合人耳的聽覺特性，具有較好的魯棒性。表2所示為相同實驗條件、不同信噪比和不同詞匯量下，基于PAFSA，AFSA的SVM語音識別正確率與HMM的識別率比較結果。表3所示是與表2相對應的錯分樣本數。

觀察實驗結果可知：基于本文提出的 PAFSASVM 模型語音識別結果與基本 AFSA-SVM 模型、HMM 識別結果相比較，在不同信噪比和不同詞匯量下，識別率均有不同程度提高，即錯分樣本數均有不同程度減少，尤其在信號的信噪比較低時，PAFSA-SVM錯分數比HMM均有減少，最大減少95個(5 dB 50詞和10 dB 50詞條件下)。這說明SVM具有很強的抗噪能力，進一步表明本文提出的小生境共享機制并行人工魚群算法是一個較為有效的 SVM參數優化方法，可使 SVM 具有良好的推廣能力和較好的魯棒性。

表2 基于AFSA，PAFSA的SVM與HMM語音識別率比較Table 2 Comparison of speech recognition rates of SVM based on AFSA, PAFSA and HMM %

表3 基于AFSA，PAFSA的SVM與HMM語音識別錯分樣本數Table 3 Comparison of error classification samples based on AFSA, PAFSA and HMM 個

5 結論

(1) 提出一種并行的人工魚群算法PAFSA，并引入小生境共享機制技術，降低錯過較優解的概率。通過對 PAFSA算法中的個體的新局部最優位置以及全局最優位置應用小生境，以維持樣本個體的多樣性，避免最優個體的流失，保證了PAFSA的求解精度。

(2) 采用測試函數對該算法進行測試和比較，驗證了其有效性。運用該算法對高斯核支持向量機參數組(C，γ) 進行優化，并將其用到一個非特定人、孤立詞、中等詞匯量的語音識別系統中，通過與基于普通AFSA-SVM和HMM的語音識別結果進行比較，證明PAFSA是一種較好的面向語音識別的抗噪SVM參數優化算法，同時也說明 SVM 在語音識別領域將會有廣闊的發展前景。

[1] Cortes C, Vapnik V. Support vector networks [J]. Machine Learning, 1995, 20(3): 273-297.

[2] 黃景德, 郝學良, 王明. 基于HMM的多態系統狀態識別模型研究[J]. 測試技術學報, 2012, 26(2): 154-157.Huang Jingde, Hao Xueliang, Wang Ming. Study of multi-state system states recognition model based on HMM[J]. Journal of Test and Measurement Technology, 2012, 26(2): 154-157.

[3] 毛健, 趙紅東, 姚婧婧. 人工神經網絡的發展及應用[J]. 電子設計工程, 2011, 19(24): 62-65.MAO Jian, ZHAO Hongdong, YAO Jingjing. Application and prospect of artificial neural network[J]. Electronic Design Engineering, 2011, 19(24): 62-65.

[4] Arun K M, Gopal M. Reduced one-against-all method for multiclass SVM classification[J]. Expert Systems with Application, 2011, 38: 14238-14248. Acta Electronica Sinica,2010, 38(7): 1626-1633.

[5] Domenico C, Rostita G. Kernel based support vector machine via semidefinite programming: Application to medical diagnosis[J].Computer & Operations Research, 2010, 37: 1389-1394.

[6] 呂卓逸, 賈克斌, 蕭允治. 低復雜度的快速降尺寸視頻轉碼算法[J]. 通信學報, 2012, 33(1): 160-166.LV Zhuoyi, JIA Kebin, XIAO Yunzhi. Fast and low-complexity video down-sizing transcoder[J]. Journal on Communications,2012, 33(1): 160-166.

[7] 蘇毅, 吳文虎, 鄭方, 等. 基于支持向量機的語音識別研究[C]//第六屆全國人機語音通訊學術會議論文集, 深圳: 哈爾濱工業大學, 2001: 223-226.SU Yi, WU Wenhu, ZHENG Fang, et al. Research of speech recognition based on support vector machine[C]// Proceedings of Sixth China Human-machine Speech Communication Conference, Shenzhen: Harbin Institute of Technology, 2001:223-226.

[8] XIE Xiang, KUANG Jingming. Mandarin digits speech recognition using support vector machines[J]. Journal of Beijing Institute of technology, 2005, 14(1): 9-12.

[9] Liu J, Wang Z, Xiao X. A hybrid SVM/DDBHMM decision fusion modeling for robust continuous digital speech recognition[J]. Pattern Recognition Letters, 2007, 28(8):912-920.

[10] 李攀, 楊瑋龍, 厲劍. 基于 DTW/SVM 的語音識別系統在DSP中的實現[J]. 電聲技術, 2006(9): 40-44.LI Pan, YANG Weilong, LI Jian. DSP Implementation of speech recognition based on DTW/SVM[J]. Audio Engineering, 2006(9):40-44.

[11] Solera-Ure?a R, Martín-Iglesias D, Gallardo-Antolín A, et al.Robust ASR using support vector machines[J]. Speech Communication, 2007, 49(4): 253-267.

[12] Maldonado S, Weber R, Basak J. Simultaneous feature selection and classification using kernel-penalized support vector machines[J]. Information Sciences, 2011, 181(1): 115-128.

[13] Huang C M, Lee Y J, Dennis K, et al. Model selection for support vector machines via uniform design[J]. Computational Statistics & Data Analysis, 2007, 52(1): 335-346.

[14] 鄧乃楊, 田英杰. 支持向量機-理論、算法與拓展[M]. 北京:科學出版社, 2009: 45-48.DENG Nanyang, TIAN Yingjie. Support vector machine- theory,algorithms and expansion[M]. Beijing: Science Press, 2009:45-48.

[15] Wang Z P, Zhao L, Zou C R. Support vector machines for emotion recognition in Chinese speech[J]. Journal of Southeast University, 2003, 19(4): 307-310.

[16] TANG Tao, GUO Qing, YANG Mingchuan. Support vector machine based particle swarm optimization localization algorithm in WSN[J]. Journal of Convergence Information Technology, 2012, 7(1): 497-503.

[17] 秦涵書, 魏延, 曾紹華. 一種基于小生境遺傳算法的 SVM參數優化方法[J]. 重慶理工大學學報, 2011, 25(12): 89-93.QIN Hanshua, WEI Yana, ZENG Shaohua. Parameter optimization of SVM for classification based on NGA[J].Journal of Chongqing University of Technology: Natural Science,2011, 25(12): 89-93.

[18] BAI Jing, ZHANG Xueying, GUO Yueling. Different inertia weight PSO algorithm optimizing SVM kernel parameters applied in a speech recognition system[C]// International Conference on Mechatronics and Automation, Changchun: IEEE,2009: 4754-4759.