某500MW汽輪機(jī)機(jī)組中壓轉(zhuǎn)子振動(dòng)特性計(jì)算分析

張 磊， 張俊杰， 徐亞濤， 趙宗彬， 秦志文

（1.神華國(guó)華（北京）電力研究院有限公司，北京100025；2.中國(guó)科學(xué)院工程熱物理研究所，北京100080）

汽輪機(jī)軸系的振動(dòng)關(guān)系到機(jī)組的安全穩(wěn)定運(yùn)行.根據(jù)國(guó)內(nèi)外軸系破壞事故調(diào)查結(jié)果的統(tǒng)計(jì)顯示［1－6］，汽輪機(jī)軸系破壞主要原因之一是在機(jī)組運(yùn)行中突然產(chǎn)生轉(zhuǎn)子彎曲，導(dǎo)致出現(xiàn)大不平衡.因此，深入研究轉(zhuǎn)子彎曲對(duì)轉(zhuǎn)子振動(dòng)特性的影響和明確額定工況及變工況對(duì)轉(zhuǎn)子不平衡的影響非常必要，可為保證運(yùn)行人員準(zhǔn)確操作提供有力指導(dǎo).

針對(duì)某500MW超臨界汽輪機(jī)機(jī)組，筆者進(jìn)行轉(zhuǎn)子經(jīng)過(guò)臨界轉(zhuǎn)速過(guò)程中安全性的研究，并對(duì)機(jī)組實(shí)際運(yùn)行中發(fā)生振動(dòng)最大的中壓轉(zhuǎn)子進(jìn)行振動(dòng)特性計(jì)算與分析.通過(guò)中壓轉(zhuǎn)子應(yīng)力場(chǎng)的計(jì)算研究，分析該機(jī)型中壓轉(zhuǎn)子彎曲對(duì)軸系振動(dòng)特性的影響，以期為工程實(shí)踐中解決不平衡響應(yīng)造成的振動(dòng)問題提供一些建議，為確定消除中壓轉(zhuǎn)子彎曲技術(shù)方案提供科學(xué)依據(jù).

1 中壓轉(zhuǎn)子臨界轉(zhuǎn)速的計(jì)算

在第2次A級(jí)檢修中發(fā)現(xiàn)，所研究的500MW機(jī)組中壓轉(zhuǎn)子彎曲嚴(yán)重超標(biāo)，對(duì)此進(jìn)行了直軸處理.同類機(jī)組的調(diào)研中也發(fā)現(xiàn)了中壓轉(zhuǎn)子在機(jī)組投運(yùn)一段時(shí)間后普遍存在不同程度的彎曲.該中壓轉(zhuǎn)子為撓性轉(zhuǎn)子，在啟動(dòng)和停機(jī)過(guò)程中均經(jīng)過(guò)臨界轉(zhuǎn)速，在臨界轉(zhuǎn)速附近，轉(zhuǎn)子不平衡響應(yīng)很大.為了保證轉(zhuǎn)子在經(jīng)過(guò)臨界轉(zhuǎn)速過(guò)程中的安全性，需要對(duì)轉(zhuǎn)子的動(dòng)力學(xué)特性進(jìn)行分析，分析轉(zhuǎn)子不平衡響應(yīng)及在3 000 r／min轉(zhuǎn)速和臨界轉(zhuǎn)速下的最大彎曲等效應(yīng)力.計(jì)算中主要考慮運(yùn)行時(shí)離心力和不平衡力在轉(zhuǎn)子上所施加的載荷，沒有考慮溫度應(yīng)力和疲勞問題，只是進(jìn)行了靜強(qiáng)度校核，故以綜合應(yīng)力（即第四強(qiáng)度理論的Von－Mises應(yīng)力）為校核標(biāo)準(zhǔn)，并從此方面說(shuō)明強(qiáng)度考核安全.

對(duì)于轉(zhuǎn)子振動(dòng)特性的分析計(jì)算，主要計(jì)算思路如下：（1）根據(jù)轉(zhuǎn)子模化理論，將中壓轉(zhuǎn)子按剛度及質(zhì)量進(jìn)行模化，通過(guò)自己開發(fā)的轉(zhuǎn)子動(dòng)力學(xué)軟件，考慮轉(zhuǎn)子的陀螺力矩效應(yīng)，分析得到中壓轉(zhuǎn)子的前幾階特征值，并畫出中壓轉(zhuǎn)子的坎貝爾圖，得到轉(zhuǎn)子的第一、第二階臨界轉(zhuǎn)速；（2）設(shè)定偏心距e為8μm、16μm、24μm、32μm和40μm 5個(gè)方案，計(jì)算與分析轉(zhuǎn)子的不平衡響應(yīng)，得到轉(zhuǎn)子在各方案下各個(gè)位置隨轉(zhuǎn)子轉(zhuǎn)速變化的響應(yīng)曲線，從而分別求得轉(zhuǎn)子在3 000r／min轉(zhuǎn)速及第一階臨界轉(zhuǎn)速下的最大彎曲靜撓度值；（3）通過(guò)靜撓度分析程序，計(jì)算不同重力加速度下轉(zhuǎn)子的彎曲值，并擬合得到轉(zhuǎn)子最大彎曲靜撓度隨重力加速度變化的關(guān)系曲線，根據(jù)最大彎曲靜撓度值等效的原理，計(jì)算得到3 000r／min轉(zhuǎn)速及第一階臨界轉(zhuǎn)速下對(duì)應(yīng)的等效重力加速度值；（4）在Ansys中通過(guò)施加等效重力加速度來(lái)模擬轉(zhuǎn)子在不同轉(zhuǎn)速下的不平衡離心力，并施加轉(zhuǎn)子的離心力載荷，通過(guò)計(jì)算分析得到3 000r／min轉(zhuǎn)速及第一階臨界轉(zhuǎn)速下的轉(zhuǎn)子等效彎曲應(yīng)力分布.

1.1 相關(guān)參數(shù)介紹

由于轉(zhuǎn)子結(jié)構(gòu)的復(fù)雜性，得到的相關(guān)參數(shù)較少，其中關(guān)于該500MW機(jī)組中壓轉(zhuǎn)子原始設(shè)計(jì)的相關(guān)參數(shù)如下：中壓轉(zhuǎn)子軸系臨界轉(zhuǎn)速為1 785 r／min；在負(fù)荷為500MW 時(shí)（轉(zhuǎn)速n＝3 000r／min時(shí)），中壓轉(zhuǎn)子前軸承轉(zhuǎn)子在x和y方向的振幅分別為87μm和73μm，后軸承轉(zhuǎn)子在x和y方向的振幅分別為93μm和47μm.雖然這些數(shù)據(jù)不能定量地驗(yàn)證計(jì)算結(jié)果的準(zhǔn)確性，但可以定性地說(shuō)明所采用方法的可行性，如通過(guò)單轉(zhuǎn)子臨界轉(zhuǎn)速應(yīng)比軸系臨界轉(zhuǎn)速低的原則來(lái)定性判斷軸承參數(shù)是否合適.

根據(jù)通用汽輪機(jī)機(jī)組的軸承參數(shù)范圍，假設(shè)該中壓轉(zhuǎn)子2個(gè)可傾瓦軸承（見圖1和圖2）的參數(shù)均相同且均為常數(shù)，其主剛度為Kxx＝Kyy＝0.7×109N／m，交叉剛度為Kxy＝Kyx＝0，主阻尼Cxx＝Cyy＝1.0×106N·s／m，交叉阻尼Cxy＝Cyx＝0.

應(yīng)用自己開發(fā)的轉(zhuǎn)子動(dòng)力學(xué)軟件，根據(jù)模化理論對(duì)該轉(zhuǎn)子進(jìn)行模化，模化后的示意圖見圖1和圖2.

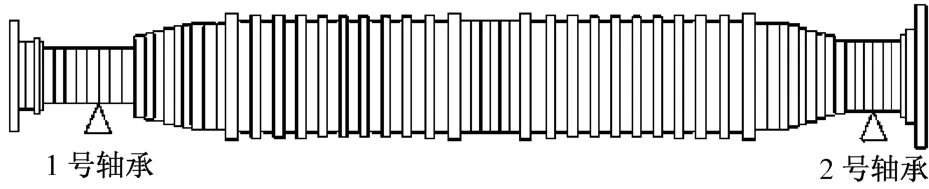
圖1 中壓轉(zhuǎn)子模化剛度直徑示意圖Fig.1 Equivalent stiffness diameter of the medium pressure rotor

圖2 中壓轉(zhuǎn)子模化質(zhì)量直徑示意圖Fig.2 Equivalent mass diameter of the medium pressure rotor

1.2 轉(zhuǎn)子臨界轉(zhuǎn)速計(jì)算分析

考慮陀螺力矩效應(yīng)后，分別計(jì)算不同轉(zhuǎn)速下的特征值，最后得到轉(zhuǎn)子的坎貝爾圖（見圖3）.由圖3可知，該中壓轉(zhuǎn)子第一、第二階臨界轉(zhuǎn)速分別為1 385r／min和3 477r／min，其中第一階臨界轉(zhuǎn)速低于軸系臨界轉(zhuǎn)速（1 785r／min），因而定性地說(shuō)明了計(jì)算結(jié)果的可信性（單轉(zhuǎn)子臨界轉(zhuǎn)速比軸系臨界轉(zhuǎn)速低）.圖4和圖5給出了該中壓轉(zhuǎn)子第一、第二階特征值對(duì)應(yīng)的振型.由圖4和圖5可知，第一、第二階特征值對(duì)應(yīng)的水平方向與垂直方向的振型基本一致.

圖3 中壓轉(zhuǎn)子彎曲振動(dòng)坎貝爾圖Fig.3 Campbell diagram of the medium pressure rotor

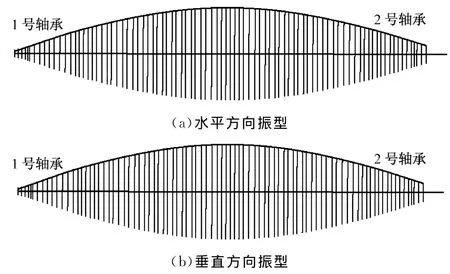
圖4 中壓轉(zhuǎn)子第一階特征值對(duì)應(yīng)振型Fig.4 First vibration mode of the medium pressure rotor

2 中壓轉(zhuǎn)子不平衡響應(yīng)計(jì)算

通過(guò)靜強(qiáng)度分析來(lái)評(píng)估轉(zhuǎn)子過(guò)臨界狀態(tài)下的應(yīng)力分布，不考慮瞬態(tài)效應(yīng)，即不考慮不平衡量引起轉(zhuǎn)子的響應(yīng)過(guò)程，僅考慮引起最大響應(yīng)后轉(zhuǎn)子彎曲危險(xiǎn)狀態(tài).轉(zhuǎn)子不平衡響應(yīng)量的大小則通過(guò)不平衡響應(yīng)計(jì)算程序來(lái)計(jì)算，即在不平衡響應(yīng)計(jì)算程序中考慮了轉(zhuǎn)子動(dòng)力學(xué)特性.轉(zhuǎn)子各節(jié)點(diǎn)的軌跡為圓形，因而在同一轉(zhuǎn)速下，從伴隨轉(zhuǎn)速旋轉(zhuǎn)的坐標(biāo)系來(lái)看，不平衡量的方向恒定，不平衡響應(yīng)引起的轉(zhuǎn)子彎曲靜撓度也是恒定的.

根據(jù)大機(jī)組軸系振動(dòng)設(shè)計(jì)導(dǎo)則，一階不平衡量等于跨內(nèi)質(zhì)量乘以規(guī)定的偏心距（8μm），但考慮到實(shí)際機(jī)組動(dòng)平衡狀況和振動(dòng)情況，其不平衡量高于國(guó)內(nèi)標(biāo)準(zhǔn).因此，設(shè)定偏心距e分別為8μm、16μm、24μm、32μm和40μm 5個(gè)方案來(lái)對(duì)比分析該中壓轉(zhuǎn)子的不平衡響應(yīng)，對(duì)應(yīng)的不平衡量分別為0.215 2 kg·m，0.430 3kg·m，0.645 5kg·m，0.860 6 kg·m和1.078 5kg·m，且將不平衡量加載到轉(zhuǎn)子的中間節(jié)點(diǎn)上來(lái)計(jì)算轉(zhuǎn)子在一階不平衡量下的響應(yīng).圖6給出了5種工況下中壓轉(zhuǎn)子1號(hào)軸承、2號(hào)軸承和中間節(jié)點(diǎn)處的響應(yīng)曲線.

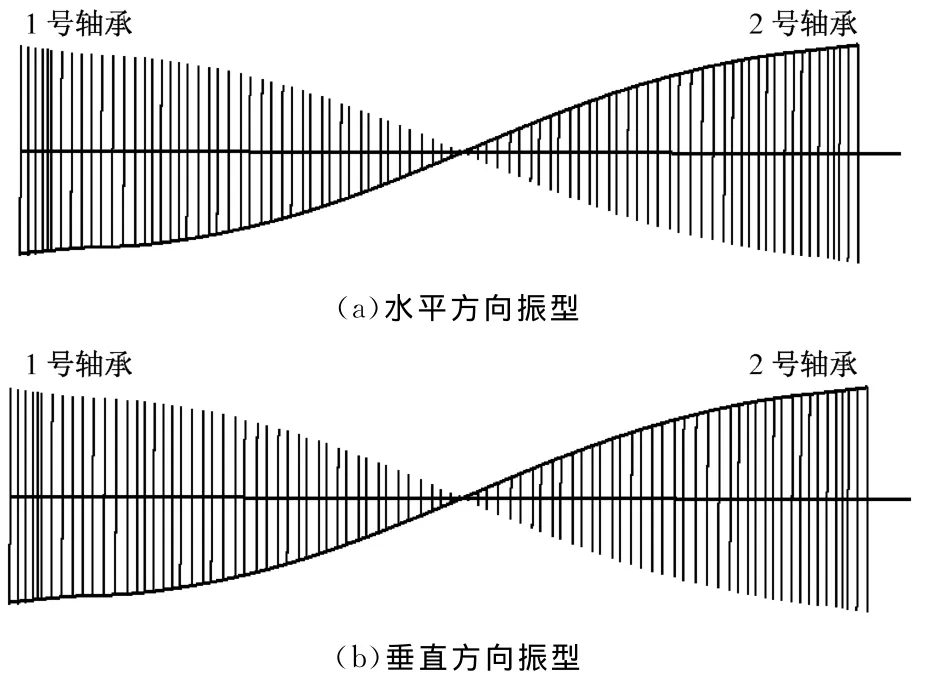
圖5 中壓轉(zhuǎn)子第二階特征值對(duì)應(yīng)振型Fig.5 Second vibration mode of the medium pressure rotor

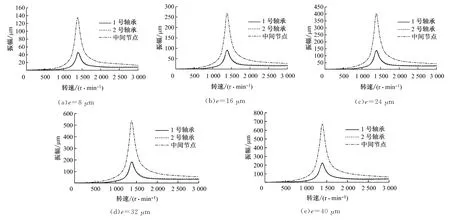
圖6 中壓轉(zhuǎn)子的不平衡響應(yīng)Fig.6 Unbalance response of the medium pressure rotor

通過(guò)中間節(jié)點(diǎn)的響應(yīng)振幅與軸承處節(jié)點(diǎn)的響應(yīng)振幅之差來(lái)計(jì)算轉(zhuǎn)子在不同轉(zhuǎn)速下的最大彎曲靜撓度，結(jié)果見表1.

由圖6可知，在額定轉(zhuǎn)速3 000r／min下，偏心距分別為8μm、16μm、24μm、32μm和40μm時(shí)，軸承處節(jié)點(diǎn)的響應(yīng)振幅分別為9.14μm、10.37μm、27.4μm、37.0μm 和45.7μm，其中偏心距為32 μm時(shí)所得到的軸承處響應(yīng)振幅較接近已知實(shí)際機(jī)組軸承處響應(yīng)振幅的平均值，因此后續(xù)的計(jì)算中均按偏心距為32μm來(lái)分析.對(duì)于一階振型，施加等效重力加速度載荷能較好地等效模擬轉(zhuǎn)子的彎曲狀態(tài).根據(jù)靜撓度計(jì)算分析程序及該中壓轉(zhuǎn)子的模化數(shù)據(jù)，計(jì)算不同等效重力加速度下中壓轉(zhuǎn)子中間節(jié)點(diǎn)的最大彎曲靜撓度，計(jì)算結(jié)果見圖7.

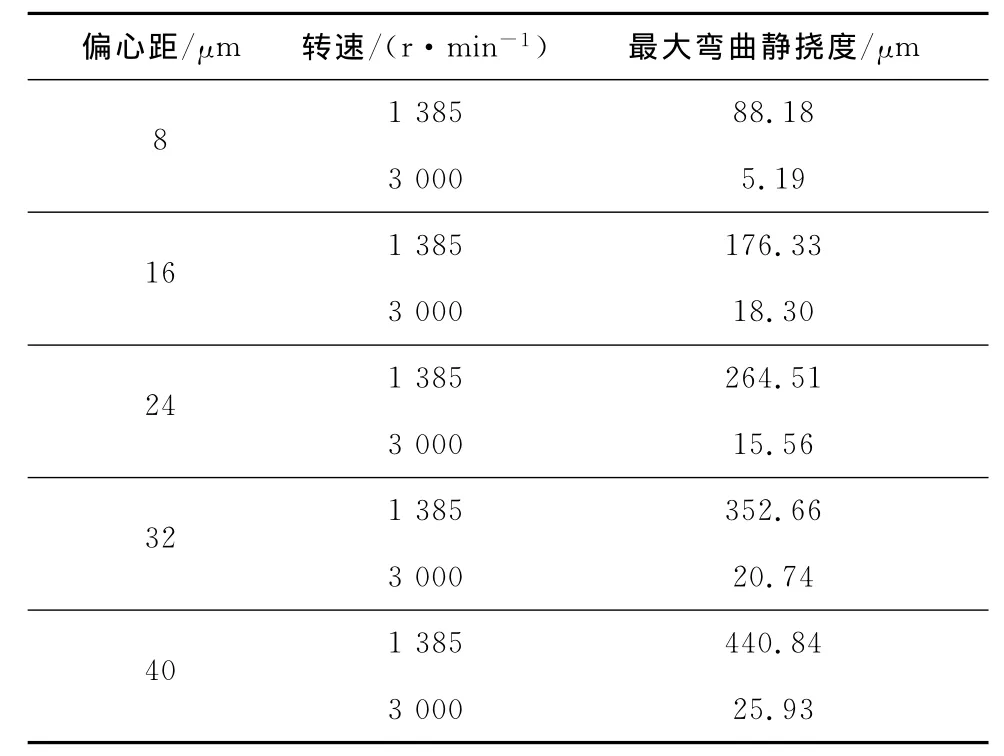
表1 不同轉(zhuǎn)速下中壓轉(zhuǎn)子的最大彎曲靜撓度Tab.1 Maximum static deflection of the medium pressure rotor at different speeds

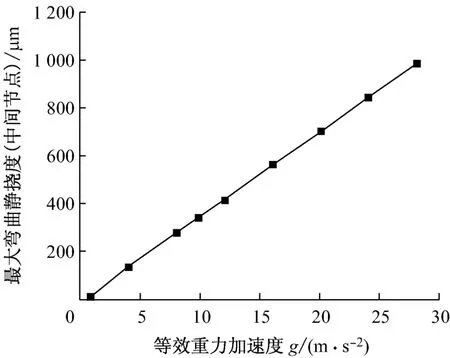
圖7 中壓轉(zhuǎn)子最大彎曲靜撓度隨等效重力加速度的變化Fig.7 Maximum static deflection of the medium pressure rotor vs.equivalent acceleration of gravity

由圖7可知，該中壓轉(zhuǎn)子在偏心距為32μm時(shí)1 385r／min和3 000r／min轉(zhuǎn)速下的不平衡響應(yīng)最大彎曲靜撓度所對(duì)應(yīng)的等效重力加速度分別為10m／s2和1m／s2.

3 中壓轉(zhuǎn)子最大彎曲等效應(yīng)力分析

為了分析中壓轉(zhuǎn)子在第一階臨界轉(zhuǎn)速及3 000 r／min轉(zhuǎn)速下的最大彎曲等效應(yīng)力，通過(guò)對(duì)中壓轉(zhuǎn)子進(jìn)行不平衡響應(yīng)分析，得到第一階臨界轉(zhuǎn)速及3 000r／min轉(zhuǎn)速下且偏心距e＝32μm時(shí)一階不平衡量下的最大彎曲靜撓度及對(duì)應(yīng)的等效重力加速度，然后通過(guò)在商用軟件Ansys的靜強(qiáng)度分析中加載葉片等效離心力、轉(zhuǎn)子旋轉(zhuǎn)角速度和等效重力加速度來(lái)分別模擬計(jì)算中壓轉(zhuǎn)子在第一階臨界轉(zhuǎn)速及3 000r／min轉(zhuǎn)速下的彎曲等效應(yīng)力.

圖8和圖9分別給出了該中壓轉(zhuǎn)子在第一階臨界轉(zhuǎn)速和3 000r／min轉(zhuǎn)速下的彎曲等效應(yīng)力計(jì)算結(jié)果.由圖8可知，在第一階臨界轉(zhuǎn)速下，轉(zhuǎn)子的最大彎曲等效應(yīng)力出現(xiàn)在末級(jí)葉輪的輪緣處，其值為39.3MPa.由圖9可知，在3 000r／min轉(zhuǎn)速下，轉(zhuǎn)子的最大彎曲等效應(yīng)力也出現(xiàn)在末級(jí)葉輪的輪緣處，該處存在一定的應(yīng)力集中，最大彎曲等效應(yīng)力為180MPa，主要是由于末級(jí)葉片的等效離心拉應(yīng)力較大所導(dǎo)致的.

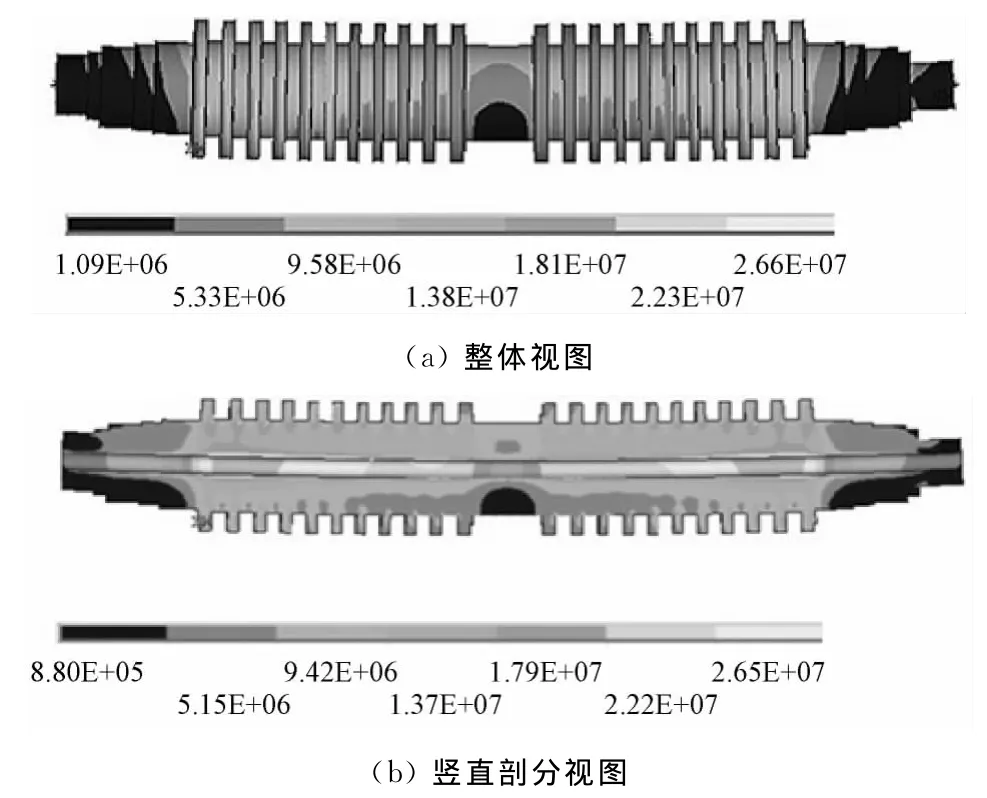
圖8 第一階臨界轉(zhuǎn)速下中壓轉(zhuǎn)子的彎曲等效應(yīng)力分布（單位：Pa）Fig.8 Equivalent bending stress distribution at the first criticalspeed（unit：Pa）

綜上分析可知，雖然中壓轉(zhuǎn)子在第一階臨界轉(zhuǎn)速下的不平衡力作用相對(duì)較大，其等效重力加速度為10m／s2，而在3 000r／min轉(zhuǎn)速下其等效重力加速度為1m／s2，但與轉(zhuǎn)速對(duì)轉(zhuǎn)子離心應(yīng)力場(chǎng)的影響相比，不平衡力作用的影響要小得多，因而3 000r／min轉(zhuǎn)速下的最大彎曲等效應(yīng)力要大于第一階臨界轉(zhuǎn)速下.根據(jù)P2鋼的高溫屈服極限Rp0.2＝420～550MPa，計(jì)算得到的各種工況下的最大彎曲等效應(yīng)力均遠(yuǎn)小于此屈服極限.

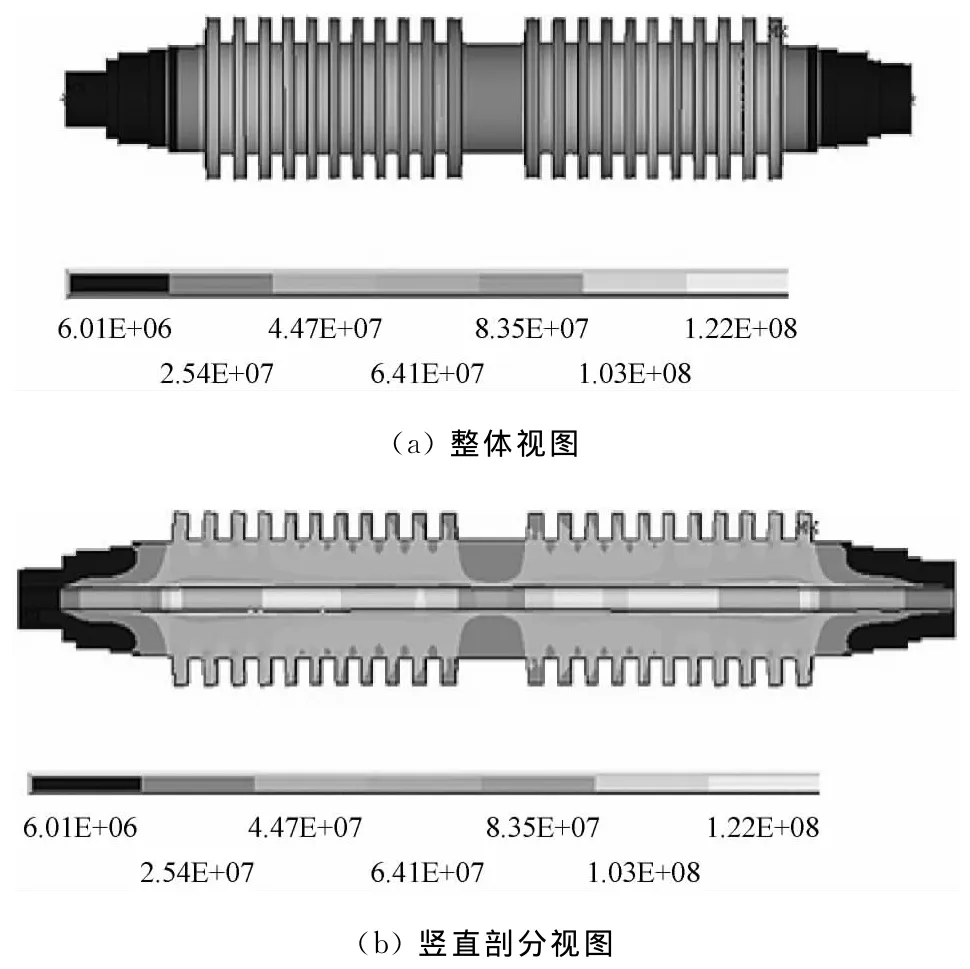
圖9 3 000r／min轉(zhuǎn)速下中壓轉(zhuǎn)子的彎曲等效應(yīng)力分布（單位：Pa）Fig.9 Equivalent bending stress distribution at 3 000r／min（unit：Pa）

4 結(jié) 論

（1）通過(guò)計(jì)算不同偏心距下的不平衡響應(yīng)，得到轉(zhuǎn)子在各工況下中間節(jié)點(diǎn)及軸承處節(jié)點(diǎn)響應(yīng)的最大振幅差，并通過(guò)靜撓度計(jì)算得到了不同重力加速度下轉(zhuǎn)子的最大彎曲靜撓度，根據(jù)最大響應(yīng)振幅差與最大彎曲靜撓度相等的原則，得到偏心距為32μm時(shí)的等效重力加速度，第一階臨界轉(zhuǎn)速和3 000r／min轉(zhuǎn)速下的等效重力加速度分別為10m／s2和1m／s2.

（2）計(jì)算得到的各種工況下的最大彎曲等效應(yīng)力均遠(yuǎn)小于該材料的屈服極限.

［1］RIBEIRO P，MANOACH E.The effect of temperature on the large amplitude vibrations of curved beams［J］.Journal of Sound and Vibration，2005，285（6）：1093－1107.

［2］陸頌元.汽輪發(fā)電機(jī)組大不平衡狀態(tài)下非線性振動(dòng)特性研究［J］.中國(guó)電機(jī)工程學(xué)報(bào)，1995，15（6）：391－396.LU Songyuan.Nonlinear vibration characteristics with large unbalance of turbogenerators rotor systems［J］.Proceedings of the CSEE，1995，15（6）：391－396.

［3］俱利鋒.帶不平衡轉(zhuǎn)子慣性激勵(lì)系統(tǒng)顫振激勵(lì)技術(shù)試驗(yàn)研究［J］.機(jī)械科學(xué)與技術(shù)，2011，30（9）：1477－1481.JU Lifeng.Testing flutter excitation with inertial excitation system［J］.Mechanical Science and Technology for Aerospace Engineering，2011，30（9）：1477－1481.

［4］朱向哲，袁惠群，張連祥.汽輪機(jī)轉(zhuǎn)子系統(tǒng)穩(wěn)態(tài)熱振動(dòng)特性的研究［J］.動(dòng)力工程，2008，28（3）：377－380.ZHU Xiangzhe，YUAN Huiqun，ZHANG Lianxiang.Study on characteristics of steady thermal vibration of steam turbine＇s rotor system［J］.Journal of Power Engineering，2008，28（3）：377－380.

［5］施維新.轉(zhuǎn)子大不平衡振動(dòng)的研究［J］.汽輪機(jī)技術(shù)，2010，52（1）：51－56.SHI Weixin.Large imbalance in the rotor vibration research［J］.Turbine Technology，2010，52（1）：51－56.

［6］盧榮軍，高偉.基于HHT的汽輪機(jī)轉(zhuǎn)子突發(fā)大不平衡振動(dòng)時(shí)頻分析［J］.汽輪機(jī)技術(shù)，2010，52（4）：305－308.LU Rongjun，GAO Wei.Time－frequency analysis of large burst unbalance vibration of turbo－generator rotator by HHT［J］.Turbine Technology，2010，52（4）：305－308.