艦船總體設計中的多學科優化技術

周 奇，陳 立，許 輝，黃衛剛

（701研究所，武漢 320064）

0 引 言

20世紀80年代，多學科設計優化（MDO）興起于航空航天領域。MDO是一種通過充分探索和利用工程系統中相互作用的協同機制來設計復雜產品及其子系統的方法論[1]。以Sobieski和Kroo為代表的科學家將其應用于飛行器結構設計中取得了良好的結果。目前，MDO廣泛應用于飛機、運載火箭、汽車、渦輪引擎及潛器的設計[2]。

對于艦船總體設計領域而言，它涉及操縱、阻力、耐波、結構、聲隱身、振動與噪聲、工藝、材料等多個方面，是一個多目標、多變量、多約束的復雜工程設計問題。這些變量可能是離散、連續或非數值的；約束可能是線性或非線性的。就傳統方法而言，船舶設計過程中對每個專業的分析是單獨進行的，設計問題是以串行設計的方法來解決，其中每個學科有不同的優化問題，這種設計過程實質上是一種順序求解，前面學科的結果往往決定后面學科的答案，而使設計陷入局部最優。

艦船是個復雜的巨系統，由很多子系統構成，各主要子系統之間均有強弱不同的耦合關系[3]。例如，改變艦船的結構設計將會改變艦船總重量，進而影響艦船的排水量、阻力及主機功率需求，同時也改變了艦船的質量分布，最終影響耐波性能、隱身性能;而改變艦船的阻力和推進特征又會影響所載燃料的重量，進而影響結構性能、空間利用情況及艦船的耐波性能。因此，為了獲得整個系統的總體最優解，合理的做法是在設計期間同時考慮船型、結構、阻力等學科的設計，給出各學科的設計變量、約束條件以及各子系統之間的耦合關系，在滿足系統總目標較優的情況下，設計各子系統，以獲得各方面的綜合平衡。多學科設計優化為艦船系統設計提供了一個有效的手段。國內將多學科優化應用于艦船總體設計的研究才剛剛起步，迄今為止還沒有形成比較成熟的理論。

1 多目標協同優化

1.1 協同優化的思想

協同優化方法屬于兩級優化算法，將優化問題分為兩級：一個系統級和并行的多個學科級（見圖1），系統級向學科級分配系統級變量的目標值，各學科級在滿足自身約束的條件下，其目標函數應使學科間耦合變量與分配的目標值的差距最小，經學科級優化后，各目標函數再傳回給系統級，構成系統級的一致性約束，以解決各學科間耦合變量的不一致。通過系統級優化和子學科級優化之間的多次迭代，最終得到一個學科間耦合關系，達到一致的系統最優設計方案。協同優化算法的本質就是系統級協調優化算法。

1.2 協同優化的應用環境

協同優化方法在求解復雜的多學科問題時能體現出優越的特性，這些求解問題有如下共性[4]：

1) 需要進行大量子學科求解的復雜系統（集成優化和單級優化更適合簡單問題）；

2) 學科間耦合度低且系統級設計變量較少；

3) 學科級優化時需要利用特殊的優化算法，如軌跡設計時的離散優化，氣動分析時的共軛優化；

4) 系統組織無嚴密的集成性。

應該注意，協同優化方法在求解時存在如下缺點：

1) 由于將狀態變量看作設計變量擴大了設計變量的維數，耗費計算求解時間；

2) 系統級優化問題的表述形式導致系統級優化十分困難，當系統級耦合變量值處于可行域之外，要使系統級和子系統級耦合變量的不一致降低為0是非常困難的，這樣要求更加完善的系統級優化算法；

3) 協同優化的收斂性目前仍未得到嚴格的證明，在實際應用中會遇到無法收斂或陷入局部最優的計算困難。

針對上述問題，許多學者從不同角度提出了一系列改進措施，包括一致性約束松弛、罰函數方法、引入響應面近似模型，系統層優化器中應用遺傳算法、混合混沌算法等現代優化算法。

1.3 多目標協同優化

多目標協同優化的系統級優化問題表述為[5]：

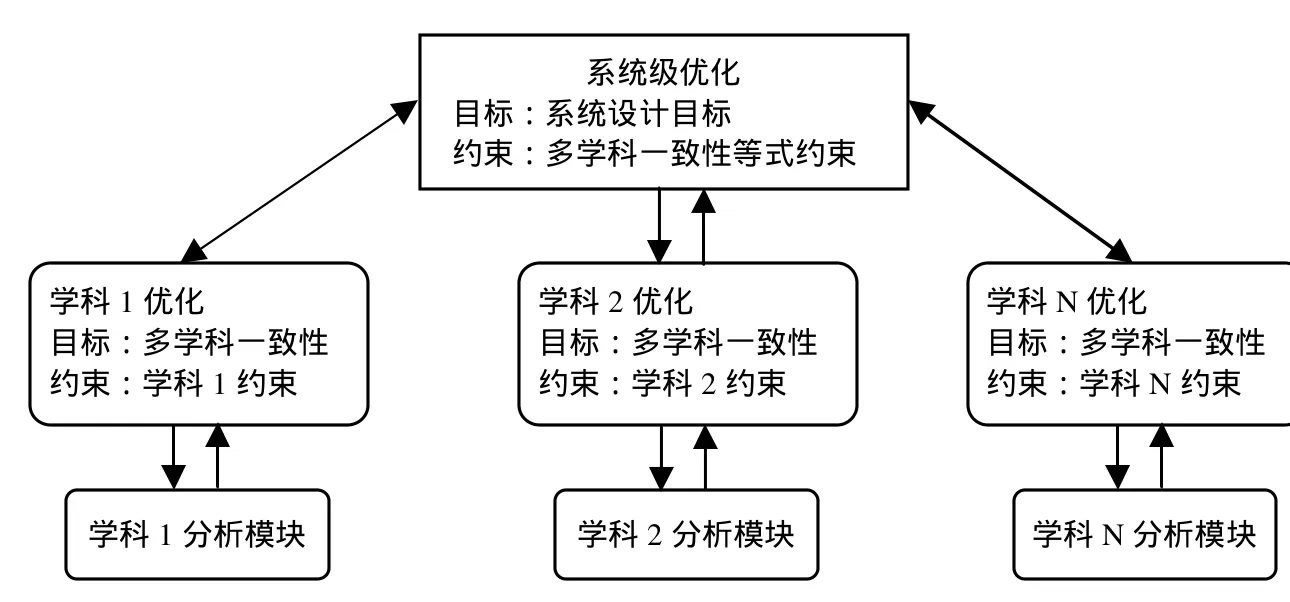
圖1 協同優化框架

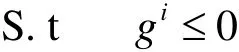
式中： Fi*——第i個學科的目標函數；x——交叉變量量 yij的輔助變量； gi≤ 0 ——局部約束條件。

由圖 2可以看出各學科專家在處理其負責的學科任務時，只需要適時將計算結果存入數據庫。并從數據庫中提取所需信息后，就可完全按該學科獲得最佳解的方向進行求解。系統層只要在消除各學科系統變量不一致性的基礎上也就可能獲得系統整體的最優解或滿意解。求解基本步驟如下[6]：

1) 求出各學科的理想解，并構造系統層優化數學模型；

2) 系統層求解，獲得輔助變量Z（系統變量）的初始協調值；

3) 在Z的初始協調值情況下，各學科引入相關變量的輔助變其一致性約束，并對其獨立變量xi、系統變量x和輔助變行求解；

4) 得到各學科計算的有關信息之后，系統層再求解Z；

5) 系統層判斷是否收斂，如收斂則結束，否則轉到步驟6）；

6) 得到Z的新的協調值之后，各學科將先前計算的各變量值作為初始值，再進行求解，然后轉到步驟4）；

7) 重復步驟3）~6）直至收斂。

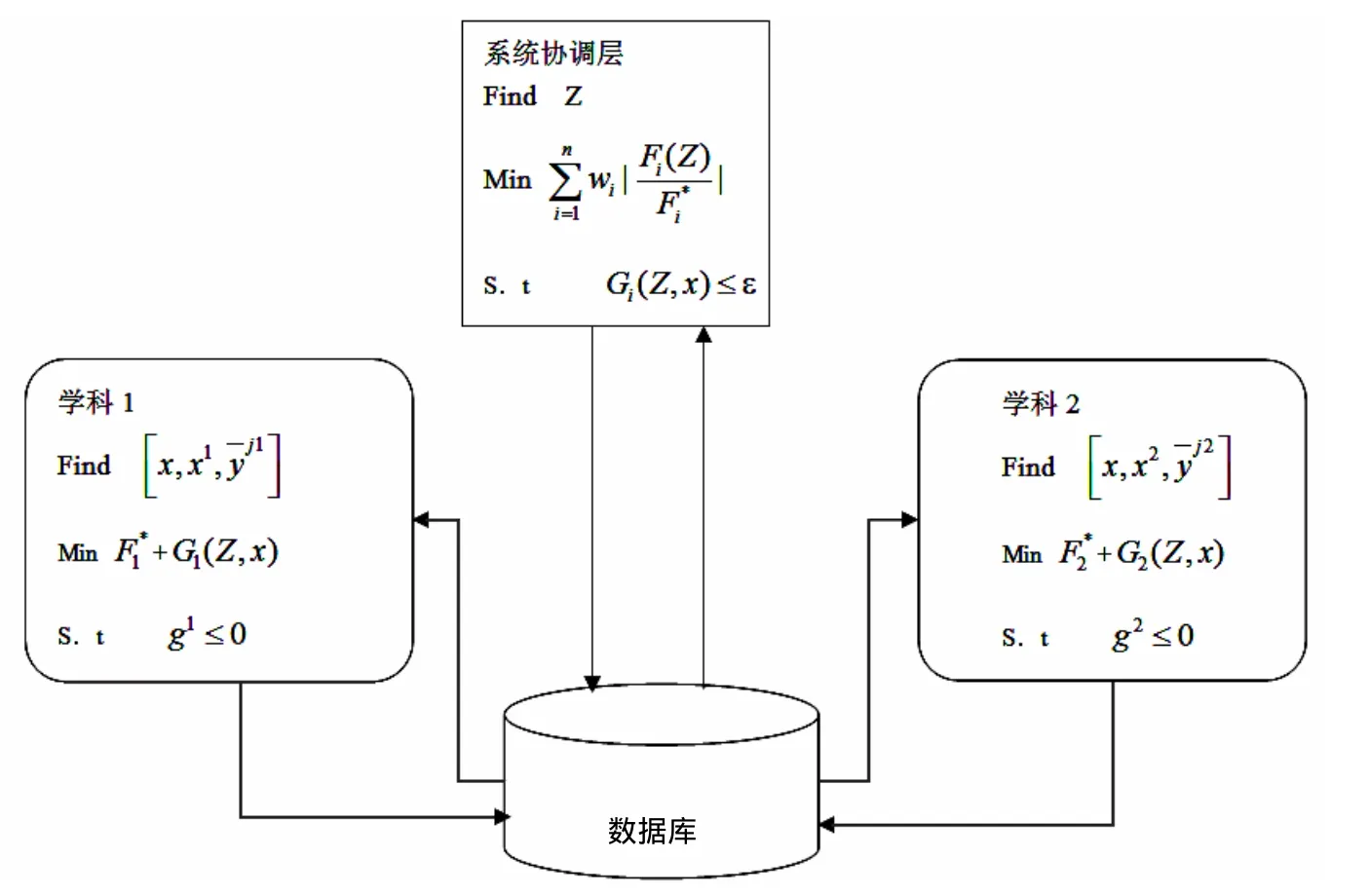
圖2 多目標協同優化流程

2 艦船總體性能多學科優化

2.1 學科分析

艦船作為一個執行一定作戰任務的復雜工程系統，進行艦船多學科優化的目的是要實現整個系統的綜合性能整體最優，將艦船總體性能優化設計分為5個學科進行學科分析。

1) 浮態與穩性子系統：對于艦船設計而言，首先要保證艦船的浮態和初穩性，它取決于船型參數（船長、船寬、吃水，方形系數等）；

2) 水動力性能子系統：水動力性能主要指快速性、耐波性、操縱性。其中快速性取決于艦船的阻力和推進性能，而阻力性能與船型參數、航速等有關。推進性能則與主機功率、轉速、螺旋槳參數（螺距、槳徑）、船型參數有關。耐波性與船型參數、航速、航向有關。操縱性與船型參數、螺旋槳參數、舵參數（舵角、舵高、舵寬）有關；

3) 造價子學科：艦船造價按照重量估算，并疊加相應的武備裝置，與船型參數、主機功率、船用材料、武備單價數量等有關；

4) 隱身子學科：艦船隱身技術作為提升艦船系統生存、突防尤其是縱深打擊能力的有效手段，與船型參數、船體布置，船用材料、螺旋槳參數等有關；

5) 振動與噪聲子學科：艦船振動與噪聲控制已成為艦船必不可少的戰技指標，與螺旋槳參數、船體布置、船用材料等有關。

2.2 設計框架

艦船學科分析時，一般采用專業的軟件進行學科分析，同時通過系統級協調共享參數。艦船總體設計優化框架如圖3所示。

圖3 艦船總體性能優化模型框架

2.3 計算環境

目前，在艦船研制領域的各學科相繼引進了各類先進的設計分析工具，如結構學科的Ansys、Nastran、Patran等；快速性學科的Fluent、Shipflow等；耐波性學科的Hydrostar等；操縱性學科的Shipma、Napa等。這些設計分析工具的使用極大提高了設計效率和分析精度，可視化的多學科優化集成平臺的建立使得這些彼此獨立的設計分析工具不再局限于學科內部。

近年來，國外很多政府研究機構、大學和開發商積極地研發多學科優化軟件框架，并取得較大的進展。現已在市場上占很大份額的集成框架有美國Engineous軟件公司開發的Isight；Phoenix Integration公司的ModelCenter、Analysis Sever；TechnoSoft公司的AML等。其中Isight占市場份額的一半。

3 結 語

本文采用 MDO設計優化思路，利用多目標協同優化算法建立了艦船總體性能優化設計框架。MDO在航空領域應用廣泛，這種將許多不同專業、約束、決策判據結合在一起的方法在艦船總體設計中的應用也會日趨廣泛。

[1] Sobieszczanski-Sobieski J, Haftka R T. Multidisciplinary Aerospace Design Optimization: Survey of Recent Developments[J].Structural Optimization, 1997, 14(1): 1-23.

[2] Charles D.McAllister. Application of multidisciplinary design optimization to racecar design and analysis[A]. 9th AIAA/ISSMO Symposium on Multidisciplinary Analysis and Optimization[C]. Atlanta, Georgia: 2002.

[3] 劉祖源，馮佰威，詹成勝. 船體型線多學科設計優化[M]. 北京：國防工業出版社，2010.

[4] Kroo,I.M.Collaborative Optimization: Status and Directions[A]. 8th AIAA/NASA/ISSMO Symposium on Multidisciplinary Analysis and Optimization[C]. Long BeachCA: 2000. AIAA-2000-4721.

[5] Shu-yan Fu,Hai-yan Huang, Zhi-xiang Lin. Collaborative Optimization of container ship on static and dynamic responses[J].Procedia Engineering, 2010, 31: 613-621.

[6] 鐘毅芳，陳柏鴻，王周宏. 多學科綜合設計原理與方法[M]. 武漢：華中科技大學出版社，2006.

[7] A. DeMiguel, W.Murray. An analysis of collaborative optimization methods[A], 8th AIAA/NASA/ISSMO Symposium on Multidisciplinary Analysis and Optimization[C], Long Beach CA, 2000. AIAA-2000-4720.