雷達目標檢測概率簡化算法及應用分析

鄭全普 張鳳偉 霍爍爍

(中國洛陽電子裝備試驗中心 洛陽 471003)

0 引言

雷達試驗是電子裝備試驗的重要項目。在雷達檢飛試驗中，檢測雷達威力即雷達作用距離是一項重要內容，分析計算的依據是統一的雷達方程和目標的平均雷達散射截面積(RCS)。雷達威力的檢測都是假定恒定的雷達散射截面積，通過這種方法，可基本實現對雷達性能的檢測和評估。但在此過程中，由于目標的散射截面積受目標起伏的影響而存在統計特性，且受目標速度、姿態和雷達頻率的影響表現出不同的統計特性，在進行雷達檢飛時，需要把不同類型的起伏目標等效到非起伏目標上。

關于雷達目標的起伏模型，最典型的是Swerling(施威林)I-IV模型，非起伏目標被稱為Swerling0或SwerlingV模型。目標的起伏降低了檢測概率，等效地降低了接收端的信噪比。而目標起伏造成的信噪比損失，通過合理的建模，可以定量分析出來。在雷達檢飛實際應用中，所采用的雷達方程就是假定目標是非起伏的，目標雷達散射截面積是平均散射截面積，在一定檢測概率條件下的，使起伏目標等效為非起伏目標，進而求出雷達的威力等。針對雷達在非起伏目標條件下的發現概率、虛警概率和信噪比之間的關系，很多文獻都有描述。本文主要針對Marcum提出的非起伏目標模型，給出了一種簡化算法，并對簡化后的誤差進行了仿真分析，并通過合理的建模，使起伏目標轉換為非起伏目標，并對轉換后的應用進行了簡要分析，這為靶場試驗的提供了理論支撐。

1 起伏目標的等效

1.1 起伏目標模型

關于起伏目標模型，文獻［1］、［2］對 Swerling起伏模型進行了系統的闡述，同時還提出了χ2分布、對數正態分布、萊斯分布等模型;文獻［3］、［4］提出采用自由度為2m的χ2分布對多種目標起伏模型進行近似，Swerling模型為m=1或2時χ2分布的特殊形式。在這些模型中，Swerling模型研究的最為廣泛和典型。其中，SwerlingI和SwerlingII型對應于多個反射體，沒有主反射體，且各個散射體單元相互獨立，SwerlingI型對應于目標的慢起伏，而SwerlingII型對應于目標快起伏;SwerlingIII和SwerlingIV型對應于存在一個主反射體和多個副反射體，SwerlingIII型對應于目標的慢起伏，而SwerlingIV型對應于目標快起伏。第一、二類模型是用于復雜目標是由大量RCS近似相等的散射體組成的情況，雖然理論上要求獨立散射體的數量很大，實際上只需四、五個即可，如飛機就屬于這一類;第三、四種模型適用于目標是有一個RCS較大的散射體和許多小散射體組成，或者一個強散射體在方位上有小的變化的情況。

1.2 目標起伏損失及等效

在雷達方程中，若目標在某距離處的回波功率等于接收機最小可檢測功率，則定義該距離為雷達最大作用距離。即

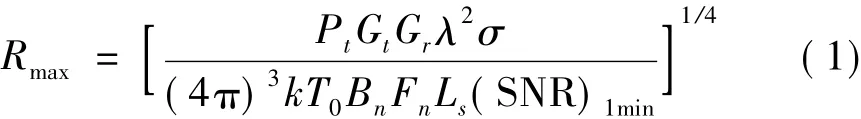
式中Pt為峰值發射功率;Gt為發射天線增益;Gr為接收天線增益;λ為波長;σ為目標截面積;k=1.38×10－23為波爾茲曼常數;T0為有效噪聲溫度，通常取290K;Bn為接收機帶寬;Fn為系統噪聲系數;Ls為雷達系統損耗;(SNR)1min為檢測目標單脈沖條件下，所需的最小信噪比。

式中假設目標的RCS恒定不變，在考慮目標起伏和脈沖積累的情況下，給出雷達方程如下:

式中，(SNR)m為積累m個脈沖時雷達檢測目標所需的信噪比;I(m)為積累改善因子。

由式(2)可知，Rmax是(SNR)m的函數。不同的起伏目標相對于非起伏目標而言，具有不同的σ和Lf。在雷達檢飛試驗中，雷達的威力是雷達在一定發現概率下的作用距離，式(2)保留Rmax、(SNR)m、σ和Lf，其它項是與雷達有關的常量，用因子K代替，雷達方程可以寫為［5］

同時，雷達的發現概率和要求的虛警概率與信噪比有關，對于典型的Swerling模型，在虛警概率為1e－6時，單脈沖條件下，信噪比和發現概率之間的關系如圖1所示。

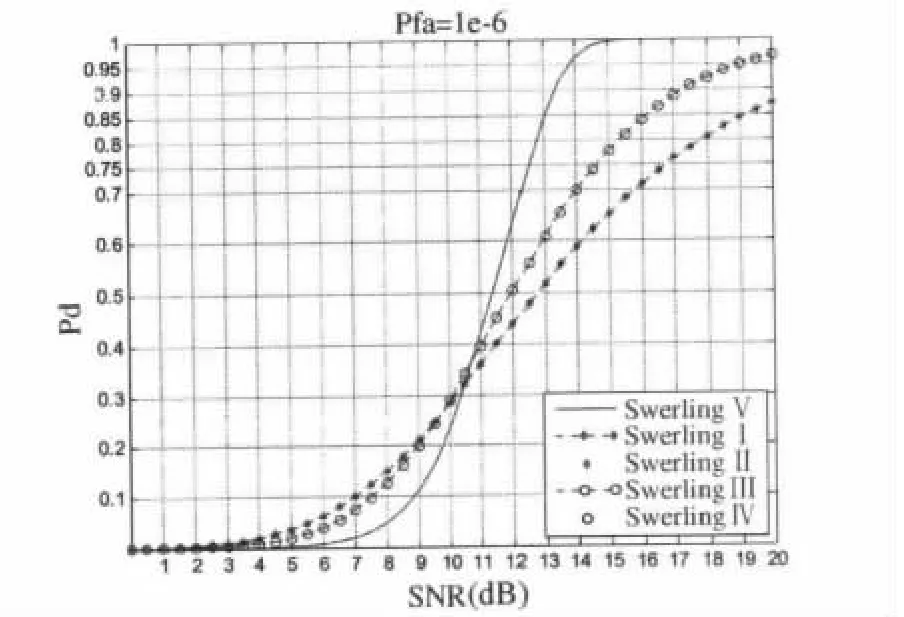
圖1 Swerling模型起伏目標和非起伏目標檢測性能曲線

從圖1中可以看出，單脈沖條件下，SwerlingI型和SwerlingII型二者曲線一致，SwerlingIII和SwerlingIV型二者曲線一致;在信噪比較大時，非起伏目標的檢測性能高于起伏目標的檢測性能，SwerlingIII和SwerlingIV高于SwerlingI型和SwerlingII型;而在信噪比較小時，具有反變的關系。在給定一個發現概率Pd時，起伏目標相對于非起伏目標存在額外的信噪比起伏損耗Lf，可以認為起伏目標等效為非起伏目標所需的額外信噪比，對應的關系如圖2所示。

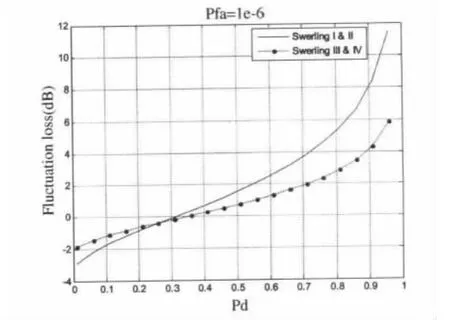
圖2 目標起伏損耗相對于檢測概率曲線

注意Lf的負值表明是起伏目標獲得SNR增益而不是損失。而對于不同虛警概率下的信噪比損失可以制成表存儲起來，在實際應用中通過查表可得到對應發現概率下的目標起伏損耗，帶入方程(3)可以求得對應起伏目標條件下，雷達的作用距離，完成對雷達威力的檢測。

2 檢測概率、虛警概率和信噪比之間的關系

檢測概率、虛警概率和信噪比之間存在固定的關系，這種關系不因雷達而異，這就為雷達設計提供了有力的參考。

2.1 推導

根據雷達原理可知，對于非起伏的目標而言，其回波信號包絡服從廣義瑞利，即萊斯(Rice)分布:

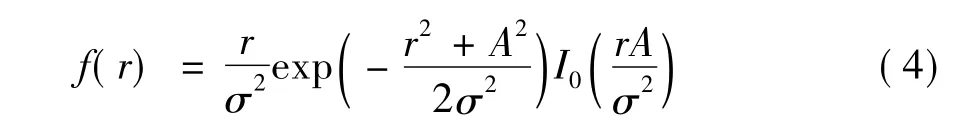
如果A/σ2=0(只有噪聲)，式(4)變成瑞利(Rayleigh)概率密度函數

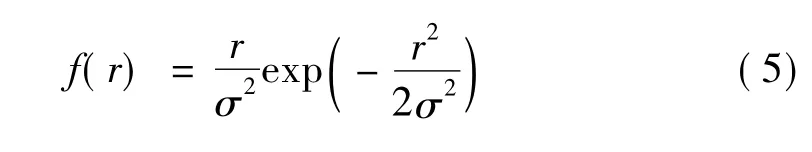
式中，A為目標的回波信號幅度(假設雷達信號為連續波);r為目標回波的綜合幅度(包括系統噪聲等);σ2為系統的噪聲信號功率;I0(β)是零階修正貝塞爾函數，定義為:

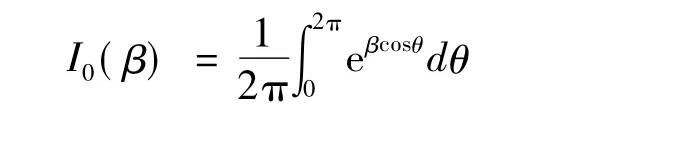
虛警概率Pfa是雷達只有噪聲出現時，回波信號超過門限VT的概率:

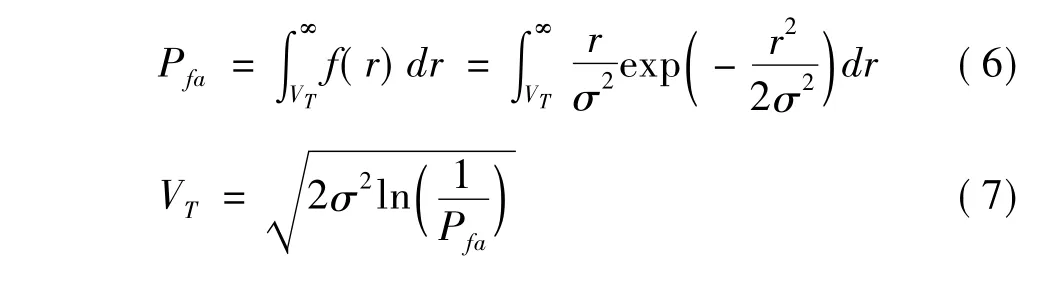
發現概率Pd是回波信號包絡超過門限VT的概率:

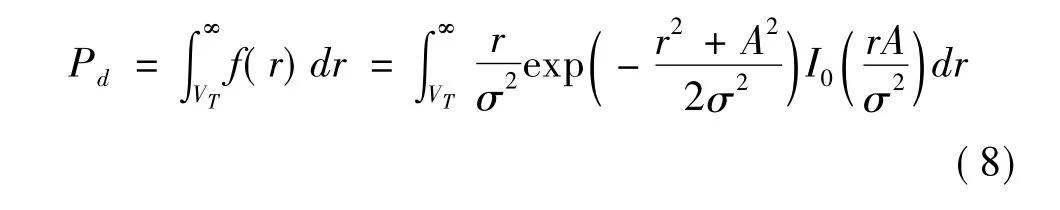
假設信號的功率為A2/2，則單個脈沖的信噪比為

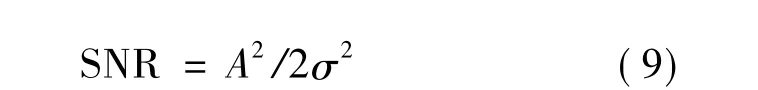
將式(8)和(9)聯立得

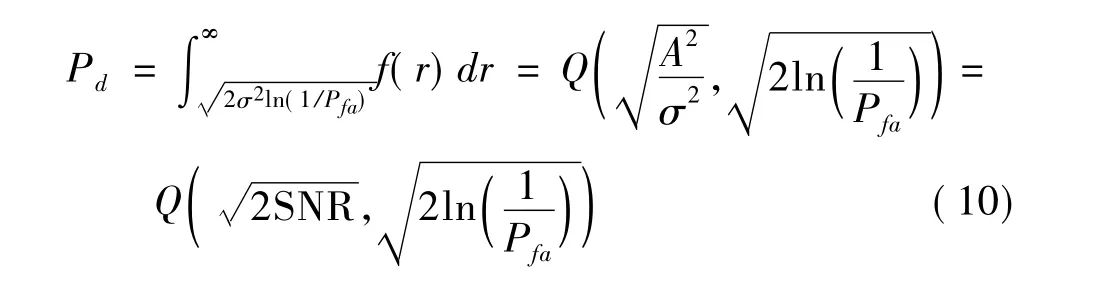
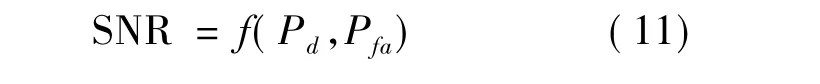
即在一定發現概率和虛警概率下所需要的信噪比，為雷達設計者提供了參考。

2.2 簡化

由于式(8)的計算過于復雜，當Pfa較小，Pd相對較大，從而門限也較大時，式(8)可以近似為

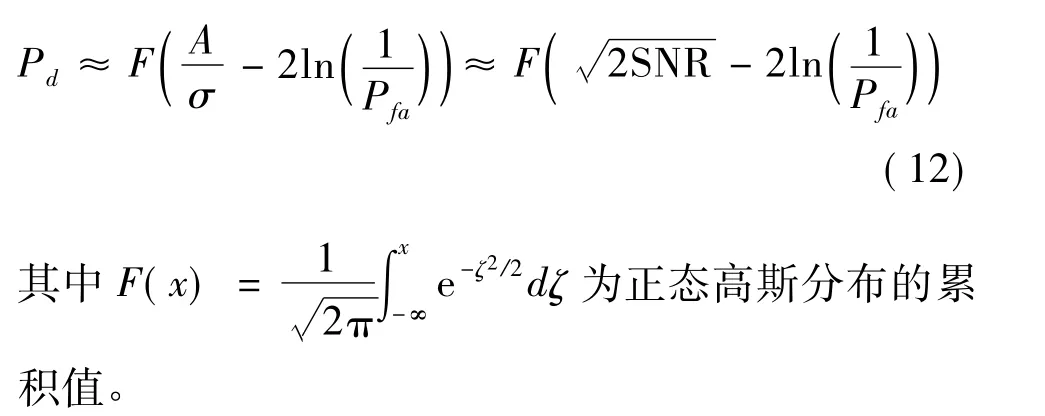
由于正態分布和補余誤差函數之間存在固定關系，針對該近似簡化方法，本文給出一種新的簡化算法如下。

已知正態分布函數的概率為

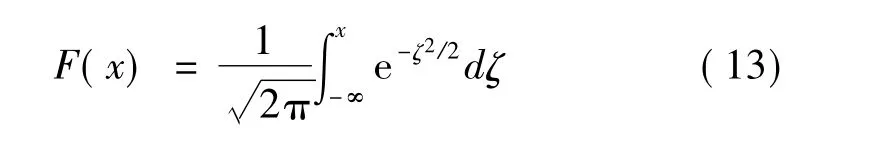
補誤差函數的概率為

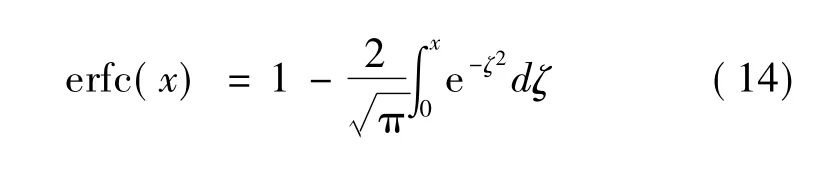
式(14)代入式(13)有如下關系成立

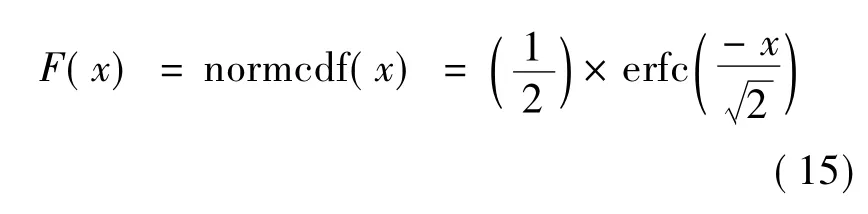
于是，式(10)可簡化為:

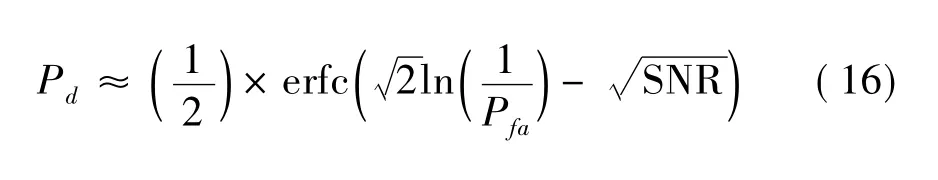
由于式(16)包含的誤差函數是一個非簡單函數，為了得到精確的雷達性能概率的估計，必須將數據制成表格或使用計算機計算。然而，存在一些數值的近似和計算技巧，使得雷達的性能估計變得簡單。補余誤差函數erfc(x)的近似方法和下限表示為［6］

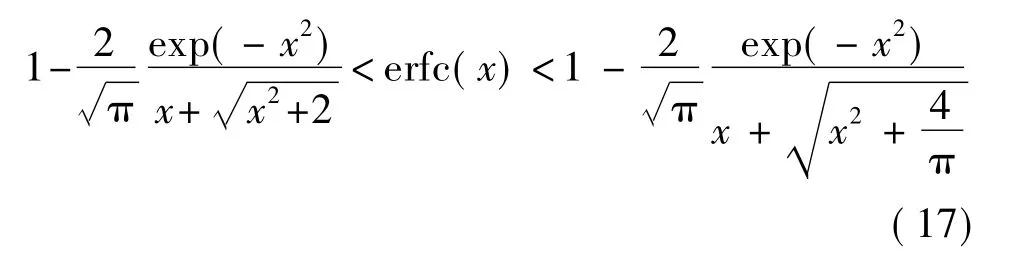
式(17)給出了erfc(x)的上下限，整個距離范圍內，下界相當緊密，而上界最好用于x＞0.8的情況。

同時，North曾提出了一個非常準確的近似［7］

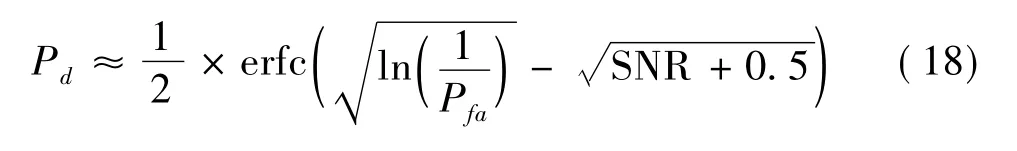
對上述方法的仿真分析如圖3所示。從圖4中可以看出，修改簡化和正態簡化具有相同的性能，North和理論值曲線基本吻合;簡化值和理論值之間存在差距;在相同信噪比條件下，簡化的信噪比較小，即在相同概率下，需要更高的信噪比。在實際應用時，應根據具體情況進行，如一般正態分布函數或補誤差函數表的形式存在，可直接查表計算。

3 結束語

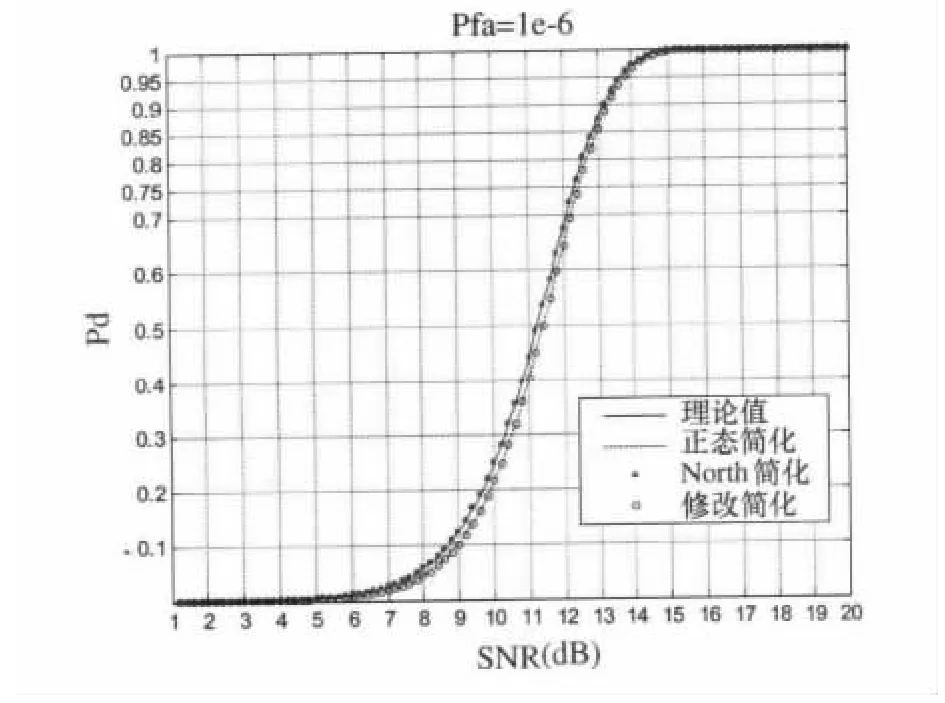
圖3 理論值和簡化值的信噪比發現概率曲線

在雷達檢飛試驗中，雷達最大作用距離和目標起伏模型因素有關，通過合理建模和推導，可以轉換為非起伏目標，此時就可以利用經典的雷達方程進行理論分析;同時，雷達的檢測端的信噪比和發現概率、虛警概率之間存在穩定關系，這種關系不因雷達而異(實際上隨著雷達采用一系列的數據處理技術，這種關系也出現了不穩定的情況，也會因雷達而異)，可以利用這種穩定的關系對雷達進行等效替代推算，即采用已有的試驗靶機作為檢飛目標，把試驗靶機的檢飛結果等效推算到對研制要求中規定目標的檢測性能上。當等效為非起伏目標時，需要考慮由目標起伏造成的信噪比損耗，通過實測數據與理論分析向比對，進一步驗證理論分析的正確性。

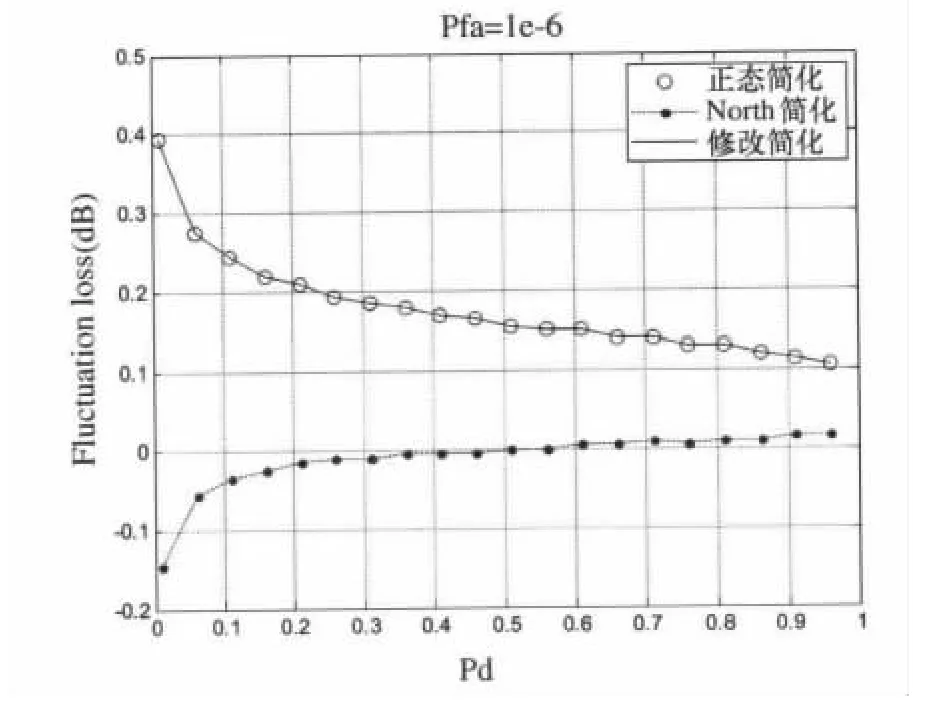
圖4 簡化模型相對于發現概率曲線

［1］丁鷺飛，耿富錄.雷達原理［M］.西安:西安電子科技大學出版社，2002，123－125.

［2］張明友，汪學剛.雷達系統［M］.北京:電子工業出版社，2006，54－58.

［3］張澄波.綜合孔徑雷達原理、系統分析與應用［M］.北京:科學出版社，1980:35－37.

［4］劉永坦.雷達成像技術［M］.哈爾濱:哈爾濱工業出版社，1999，35－37.

［5］趙志超，饒彬，王濤等.雷達網檢測概率計算及評估［J］.現代雷達，2012，(7):7－10.

［6］Mark A.Richards.Fundamentals of Radar Signal Processing［M］.2004，105－107.

［7］North D.O，An Analysis of the Factors which Determine Signal/Noise Discrimination in Pulsed Carrier Systems［C］.Proc.IEEE 51，1963，(7):1015－1027.