某型教練機機載天線與雷達罩的射線入射角的計算

張超超

（中航工業洪都，江西南昌330024）

0 引言

雷達罩是電磁波的窗口，其作用是保護天線，防止環境對雷達天線工作狀態的影響和干擾，從而減少驅動天線運轉的功率，提高其工作可靠性，保證雷達天線全天候工作。雷達罩的存在，延長了天線的使用壽命，簡化了天線的結構，減輕了結構的重量。雷達罩作為雷達系統的重要組成部分，其性能好壞直接影響到雷達系統的能。可以說，雷達罩與天線同等重要。要求雷達罩對天線的電磁輻射特性的影響最小，并且滿足戰術技術指標的要求。雷達罩技術綜合了材料、工藝、機械、電磁、空氣動力學和結構力學等學科的知識，設計和制造難度較大。由于雷達罩工作在一種復雜的特殊環境中，對材料的要求十分苛刻，主要使用玻璃纖維復合材料。國外出現了抵御反輻射導彈襲擊的防彈天線罩，能抗高速破片和沖擊波的打擊。

由于空基天線罩是空基電子系統不可缺少的組成部分，其電磁特性的優劣與系統的整體性能密切相關，長期以來，帶罩天線的特性分析和天線罩的結構設計一直受到人們廣泛的關注。解析法(AM)以幾何光學(GO)為基礎，通過射線對罩壁入射角的加權平均等效來計算各站位點的罩壁厚度，方法簡便有效，并適用于非均勻壁厚天線罩的設計，是一種工程中普遍采用的設計方法。

本文主要運用投影、向量、曲線擬合等數學思想，通過MATLAB工具計算分析機載天線的入射角大小，與雷達罩的標準指標進行比較，確定雷達罩的電性能是否最佳。并應用于某型教練機XXX火控雷達罩。

1 問題來源描述

某型教練機火控雷達罩如圖1所示，其雷達罩表面點的三維坐標見圖2。

圖1 某型教練機火控雷達罩

圖2 原始數據點的三維空間分布

將橢圓處放大，我們可以清晰地看到4種顏色的點，即為4個數據文件在空間中的表示，如圖3所示。

現需要求得初始點（即為機載天線上的點）到所給數據點的連線與所給數據點所在切面的法線所成的夾角，要求對于所給范圍內任意的初始點，每個數據點對應的角度小于70°。但是切面無法求得，故而把問題轉化為求初始點到所給數據點的連線與所給數據點所在擬合曲線的切線的法線所成的夾角,如圖4所示。

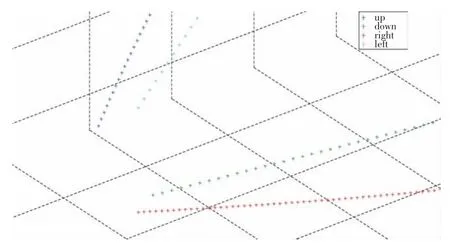
圖3 橢圓處放大圖

圖4 所求夾角示意圖

2 問題詳細解決方案

2.1 數學思想

2.1.1 二維空間的曲線擬合

曲線擬合(curve fitting)（見圖5）是指選擇適當的曲線類型來擬合觀測數據，并用擬合的曲線方程分析兩變量間的關系，用解析表達式逼近離散數據的一種方法。

圖5 二維曲線擬合

在科學實驗或社會活動中，通過實驗或觀測得到量x與y的一組數據對(xi,yi)(i=1,2,…,m)，其中各xi是彼此不同的。人們希望用一類與數據的背景材料規律相適應的解析表達式，y=f(x,c)來反映量x和y之間的依賴關系，即在一定意義下“最佳”地逼近或擬合已知數據。f(x,c)常稱作擬合模型，式中c=(c1,c2,…cn)是一些待定參數。當c在f中線性出現時，稱為線性模型，否則稱為非線性模型。

最小二乘法是曲線擬合的核心算法，是一種數學優化技術，它通過最小化誤差的平方和找到一組數據的最佳函數匹配。很多其他的優化問題也可通過最小化能量或最大化熵用最小二乘形式表達。

比如從最簡單的一次函數y=kx+b講起，已知坐標軸上有些點(1.1,2.0),(2.1,3.2),(3,4.0),(4,6),(5.1,6.0),求經過這些點的圖像的一次函數關系式。當然這條直線不可能經過每一個點，我們只要做到5個點到這條直線的距離的平方和最小即可，這就需要用到最小二乘法的思想。

2.1.2 空間曲線投影

空間曲線投影就是通過空間曲線每一點向坐標作垂線，這個垂線與坐標面的交點集合就是投影，投影是一條曲線，如果想投影到xy平面，只需令。

一個簡單的例子：空間直線方程：x=y=z，投影到xy和xz平面后，如圖6所示。

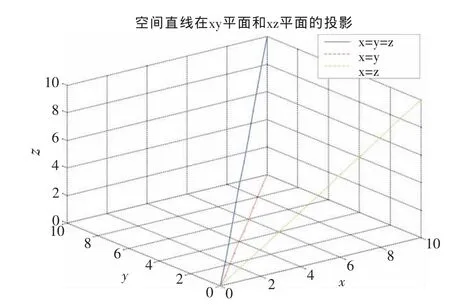
圖6 在xy、xz平面的投影

2.2 設計解決方法

2.2.1 角度求解方法

眾所周知，要求得兩條線段之間的角度，有很多種方法，最簡單的比如：用量角器、三角形的余弦公式。顯然用量角器的方法過于笨重和簡單，余弦公式過于復雜，在這里都不方便。這是抽象的數據，而且需要批量式的得到入射角，所以需要用到工程化編程的思想，把問題細化、簡單化，把這個問題轉化為求兩條線段之間夾角。

為了使得到的結果更加高效、快速、簡便，在這里運用數組的思想，把三維數據點坐標放到一個數組中，即一個向量，通過求解兩個向量之間的夾角（見圖7）來得到所需結果。

求得，即

在MATLAB中可通過內置的函數dot，norm，

求得α角。

圖7 兩向量之間的夾角示意圖

2.2.2 三維空間的擬合曲線

二維空間的擬合曲線方程在MATLAB上可以通過polyfit，polyval命令得到，但是沒有關于三維空間擬合曲線的求解函數。運用投影的思想，我們先將三維空間曲線投影到xy平面，得到xy平面的擬合曲線方程，有了擬合曲線方程，通過求導法，就能得到關于xy平面在擬合點的切線斜率，同理，再將三維空間曲線投影到xz平面，得到關于xz平面在擬合點的切線斜率，由此可得，關于空間曲線在擬合點的切線向量為

有了擬合曲線方程，就可以通過原始數據的x坐標，求出擬合點的坐標，然后得到初始點到擬合點的向量vectorinitial，我們稱之為初始向量。

曲線擬合后，“問題來源描述”一節中的橢圓處放大見圖8。

圖8 曲線擬合后，橢圓處放大圖

2.3 最終計算結果及分析

通過向量求角公式，可以得到初始向量與切線向量的夾角α，但是我們需要的最終計算結果是初始向量與切線的法線做成的夾角vectorα，所以還需要做一個判斷，如果α＜90°，則vectorα=90°｜α，如果α＞90°，則vectorα=α｜90°。

最終角度結果趨勢見圖9。

圖9 最終角度結果趨勢圖

由圖可知，雷達罩長度60之后，4條數據線都超過了70°，故此雷達罩沒達到要求。整個計算過程所需時間如圖10所示，t_end=8.3118s。

圖10 最終計算時間

2.4 誤差分析

因為初始點與擬合點的差異，誤差必然是存在的。經初步分析，如果初始點與擬合點距離越大，數據點所覆蓋的雷達罩跨度越短，允許的角度上限α越小， 那么誤差越大。令k=1，則誤差在允許范圍內。 誤差分析見圖11。

圖11 誤差分析圖

3 結語

對型號雷達罩進行初始數據錄入后，再對機載天線與雷達罩的射線入射角進行計算分析。該方法具有普遍性，幾乎對所有型號教練機的雷達罩都能適用；而且還具有快速性，對于大量的成批數據，從數據導入，圖形、誤差分析，到最終結果一目了然只需短短8.3秒就能完成；同時還具有實用性，雷達罩價格昂貴，將該方法應用于檢測性能環節上，可以有效判斷其性能是否符合指標，減少廢品率，從而節約成本，有效控制了機載雷達罩的選擇，保證了飛機質量。以后還可以作進一步的改進，如提供友好的人機交互界面、完整的數據輸入和圖形顯示，以方便用戶的使用，提高工作效率；或者通過后臺編程，把此功能直接嵌入到CATIA中，讓用戶在使用CATIA分析飛機雷達參數時直接得到所需結果；使誤差分析更準確或者將誤差降至更低。

[1]萬國賓，趙惠玲.機載天線與天線罩的設計與電磁特性分析.制造業自動化，2009.

[2]陳杰.MATLAB寶典,2007.1.