地震拖纜的復模態振動主動控制

張 亮，張維競，劉 濤

(上海交通大學海洋工程國家重點實驗室，上海 200030)

在海洋石油勘探中，拖曳陣列被廣泛使用。海洋地震勘探由一個拖曳船，一組零浮力拖纜和探測控制設備等組成。為探測由海底返回的聲波，在拖纜上均勻分布著水聽器組。國際上，目前拖纜的長度一般為3 000 m左右，一個典型的拖曳形狀如圖1所示。在拖曳的時候，拖纜由深度控制器(水鳥)控制，通常情況下這些控制器沿拖纜每隔100～300 m布置一個。

拖纜系統的動力學模型已經被數位學者研究過，例如Dowling，Triantafyllou G，Chryssosdis［2］，Pedersen E，Sorensen［3］，Svein Ersdal［4］，上述學者主要研究了拖纜系統的線性化模型。Tu Duc Nguyen［5］基于邊界測量，設計了指數穩定的觀測器，同時利用觀測器和邊界測量的信息，設計了一個指數穩定的控制器。段磊，張小卿［6-7］設計了一種新的控制拖纜姿態的控制器，可以在深度和水平方向控制拖纜。劉濤，張維競［8-9］基于lyapunov方法研究了拖纜系統主動振動控制規律。上述控制規律方面的研究都主要集中于拖纜系統的運動穩定性，在抑制拖纜系統振動性能方面的研究文獻還比較少見。

圖1 海上地震勘探系統Fig.1 Marine seismic surveying system

實模態控制方法是一種發展較為成熟的技術，但由于地震拖纜的重阻尼特性，采用比例阻尼來代替實際阻尼特性的近似方法，不能真實反映地震拖纜系統的動力特性，從而使得實模態主動控制策略難以實施。因此，首先建立了地震拖纜系統的有限元模型，基于模態觀測器，在獨立復模態空間，通過選擇合適的權重矩陣，對地震拖纜的低階模態，設計了穩定的最優控制規律。

1 拖纜系統運動方程和有限元模型

地震拖纜系統的線性化模型［4］:

式中:m表示單位纜長的質量與其附加質量之和;Q(x)=T(x)-aU2，U表示拖曳速度，a表示單位纜長的附加質量;T(x)=T0+ft(l-x)，T0是拖纜尾端張力，ft=0.5ctρπdU2，ft表示單位纜長切向水阻力，ct表示切向水阻力系數;l表示拖纜的長度，ρ表示海水的密度，d是拖纜的直徑;a1=2aU;fn=0.5cnρπdU2，fn表示單位纜長法向水阻力，cn表示法向水阻力系數。

使用有限元方法能夠將上述控制方程離散，得到系統的有限元模型，詳細的有限元建模可參考文獻［4］。

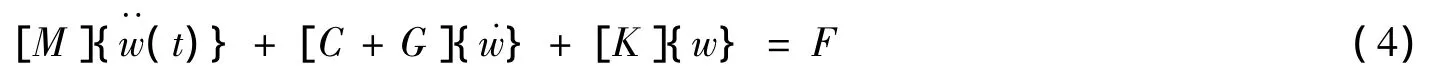
式中:M表示n×n質量矩陣，C是n×n線性化水阻尼矩陣，G是由拖纜的軸向運動引起的n×n陀螺阻尼矩陣，K是n×n系統的剛度矩陣，F表示n×1節點力向量，能被分解為

式中:Fc表示由水鳥提供的控制力，Fd表示擾動力。

2 控制描述

將系統的有限元模型轉化為狀態空間模型，令

其中，yi表示拖纜垂向速度，yn+1表示拖纜垂向位移 。

則可以將式(4)寫成

上式是一組2n個耦合的一階常微分方程。

應用左右特征向量的雙正交性［10］，可解耦上述方程。

使用下面的線性變換，原狀態向量X(t)能夠被轉換到模態坐標

其中，R就是右模態矩陣。利用雙正交性可以獲得下列一組解耦的模態方程

其中，Q(t)=LTBV(t)，L是包括左特征向量的實部和虛部的模態矩陣。模態矩陣L，R滿足LTR=I。方程(10)包括n對下列形式的解耦的模態方程

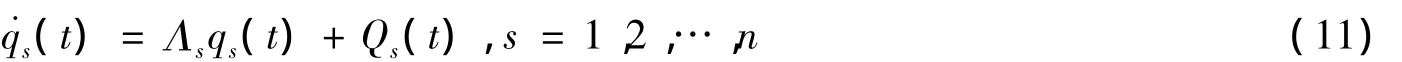
3 最優獨立模態空間控制

控制的目標是最小化系統的響應。最優獨立模態空間控制通過最小化目標泛函得到

其中，Js是穩態系統響應的獨立模態泛函，k是被控的模態數。

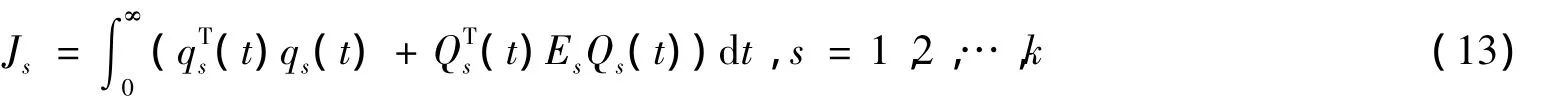
其中，Es是權重矩陣。

從最優控制理論可以得到最優的獨立模態控制力是

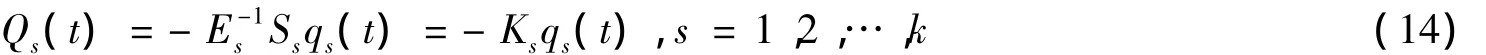
其中，Ks為最優控制器設計的反饋增益矩陣，Ss可以通過求解下面的Riccati方程獲得

Riccati矩陣是一個2×2矩陣，由于矩陣的對稱性，對每一個僅僅需要求解3個元素。在地震拖纜控制系統中，水鳥提供的控制力正比于水鳥中電機所消耗的能量，即式(13)中的第二項代表的是水鳥的能耗。

權重矩陣Es如果選擇不當［11］，可能會導致閉環系統的不穩定。采用新的設計方法［11-12］使用一個具有相對角同元素的對角權重矩陣Es=diag(Es11，Es11)能保證系統的穩定性，相應的最優控制的Riccati方程的解就變為:

則最優獨立模態空間控制的控制輸入為

在計算反饋控制力時需要精確的模態狀態，因為深度傳感器的測量是實際的位移和速度，需要將傳感器的讀數轉換為模態狀態參數。這可以通過觀測器或者模態濾波器實現，模態濾波器有眾多的優點，但進行模態濾波時需要較多的傳感器，實際的拖曳系統的傳感器數目較少，因此可以通過狀態觀測器實現傳感器的讀數到模態狀態參數的轉換。

4 數值仿真

通過數值計算可驗證上述控制策略的有效性。仿真長度為900 m的拖纜，有限元模型共有90個元素，即n=90。拖纜系統運動方程的初始條件為:φ(x)=sin(2πx/900)，φ(x)=0。仿真使用的數據見表1。

表1 拖纜系統參數Tab.1 Parameters of towed seismic cable

由于拖纜張力為一沿拖纜長度變化的量，為了更有效地控制拖纜系統的動態行為，在250 m、450 m、600 m和800 m處配置水鳥。選擇250 m和600 m處的水鳥控制拖纜的第一階模態，450 m和800 m處的水鳥控制第三階模態。對400 m拖纜處施加一個沖擊載荷，圖2給出了550 m處拖纜系統的響應，由圖可以看出與未控制拖纜相比，在550 m處被控制拖纜有較好動態響應。

圖3給出了4個水鳥的作用力變化圖。各水鳥提供的作用力完全在現有水鳥能夠提供的變化力范圍之內。由圖3(a)、(b)可見，在拖纜張力較大的前端，也就是250、450 m處的水鳥對外擾施加的作用力較大，但能夠較快地收斂到零，而處于拖纜張力較小的尾部，也就是600、800 m處的水鳥，雖然需要施加的作用力較小，但卻需要較長的時間才能收到零，這些是和實際情況相符合的。

圖2 550 m處拖纜的位移響應Fig.2 Displacement response of seismic cable at 550 m

圖3 不同位移水鳥的作用力Fig.3 Force provided by bird

圖4給出了拖纜前三階模態的變化圖。從圖4(a)、(c)可以看出，由于對第一、三階模態施加了控制力，這兩階模態得到了較好的抑制;而從圖4(b)可以看出，第二階模態非但沒有得到抑制反而有所增強，這是由第一、第三階模態的控制力溢出引起的。

圖4 拖纜前三階模型變化Fig.4 Response of the first three mode

5 結語

對地震拖纜的振動主動控制進行了初步研究。由于地震拖纜系統的重阻尼特性，使得用比例阻尼近似實際拖纜阻尼特性將產生較大誤差，為解決無法在實模態空間進行有效的控制策略設計問題，基于拖纜系統的有限元模型，在拖纜系統的復模態空間，使用兩個作動器(水鳥)控制拖纜系統的一階復模態，設計了穩定的最優復模態控制規律。數值仿真的結果表明，通過由水鳥提供的控制力控制拖纜系統的第一、三階模態，能夠快速地抑制一、三階模態的振動，但是控制力也會溢出到第二階模態，因此如何有效地減少控制溢出的問題是下一步工作的重點。基于復模態的地震拖纜最優控制策略，綜合考慮了水鳥耗能和抑制拖纜振動，在最大程度地利用水鳥自帶電池能量的基礎上，有效地抑制拖纜振動，既能減少水鳥更換頻率，又能提高地震勘探數據采集質量，進而提高勘探作業的效率。

［1］ Dowling P.The dynamics of flexible slender cylinders，part 1:Neutrally buoyant elements［J］.Journal of Fluid Mechanics，1988(187):507-533.

［2］ Triantafyllou G S，Chryssostomidis C.The dynamics of towed arrays［J］.ASME Journal of Offshore Mechanics and Arctic Engineering，1989:208-213.

［3］ Pedersen E Sorensen.A modeling and control of towed marine seismic streamer cables［C］∥Proceedings of the IFAC Conference on Systems and Control.2001.

［4］ Svein Ersdal，A experimental study of hydrodynamic forces on cylinders and cables in near axial flow［D］.Norway:Norwegian University of Science and Technology，2004.

［5］ Tu Duc Nguyen O.Egeland stabilization of towed cables［C］∥Proc.of the 43rd IEEE Conference on Decision and Control.2004.

［6］ DUAN Lei，ZHANG Wei-jing.A new device for controlling the position of marine seismic streamer cables［C］//Proceedings of the ASME 2010 29th International Conference on Ocean，Offshore and Arctic Engineering.2010:111-118.

［7］ ZHANG Xiao Qing，ZHANG Wei-jing，CHEN Jun.Experimental study on hydrodynamic characteristics of hydrofoil of the birds embedded in marine seismic streamers［C］//Proceedings of the ASME 2010 29th International Conference on Ocean，Offshore and Arctic Engineering.2010:105-110.

［8］ 劉 濤，張維競.基于LYPUNOV方法的信息拖纜水平振動的控制研究［J］.上海交通大學學報，2010，44:1460-1464.

［9］ LIU Tao，ZHANG Wei-jing，MA Jie.Adaptive vibration control of towed seismic cable［C］//ASME 2011 30th International Conference on Ocean，Offshore and Arctic Engineering(OMAE2011).2011:239-248.

［10］ Meirovitch.Dynamics and Control of Structures［M］.New York:John Wiley，Sons Inc，1992.

［11］ LIN Y H，CHU C L.A new design for independent modal space control of general dynamic systems［J］.Journal of Sound and Vibration，1995，180:351-361.

［12］ LIN Y H，HUANG R C，CHU C L.Optimal modal vibration suppression of a fluid-conveying pipe with a divergent mode［J］.Journal of Sound and Vibration，2004，271:577-597.