某新型火炮發(fā)射過程建模與仿真
劉圣杰,張相炎
(南京理工大學(xué)機(jī)械工程學(xué)院,江蘇南京 210094)
0 引言
現(xiàn)代戰(zhàn)爭(zhēng)對(duì)火炮的綜合性能提出很高的要求,但是火炮的威力與機(jī)動(dòng)性能等條件通常是相矛盾的。如何協(xié)調(diào)好它們之間的關(guān)系,是提高火炮綜合性能的關(guān)鍵。根據(jù)無后坐力炮與膨脹波火炮在發(fā)射過程中都有火藥氣體流出的技術(shù)特點(diǎn),提出了一種新型火炮,在火炮發(fā)射過程中的某一膛壓下使火藥氣體向后噴出,產(chǎn)生一個(gè)向后作用的沖量,這樣起到協(xié)調(diào)火炮威力與機(jī)動(dòng)性能的關(guān)系。該炮的發(fā)射過程不同于無后坐力炮與膨脹波火炮,本文針對(duì)其特點(diǎn)建立其發(fā)射模型,并分析其發(fā)射性能。
1 物理模型
該型火炮采用半可燃藥筒,發(fā)射時(shí)藥筒卡在膛內(nèi),火炮發(fā)射過程中火藥燃燒膛內(nèi)壓力增大,當(dāng)達(dá)到半可燃藥筒金屬筒底的許用剪應(yīng)力時(shí),半可燃藥筒被剪斷,在高膛壓下,半可燃藥筒的金屬筒底與火藥氣體同時(shí)向后噴出。其發(fā)射過程可以分為以下幾個(gè)階段:第一階段,底火點(diǎn)燃發(fā)射藥,達(dá)到彈丸的啟動(dòng)壓力后推動(dòng)彈丸向前運(yùn)動(dòng),這一過程與普通閉膛火炮一樣;第二階段,當(dāng)膛壓到達(dá)半可燃藥筒金屬筒底的剪斷條件時(shí),金屬筒底被剪斷后火藥氣體噴出,膛內(nèi)火藥氣體流動(dòng)狀態(tài)發(fā)生改變,膛內(nèi)壓力迅速下降,同時(shí)彈丸繼續(xù)向前運(yùn)動(dòng),直到出炮口;第三階段,即彈丸出炮口后的后效期階段。
圖1是根據(jù)該新型火炮的特點(diǎn)而簡(jiǎn)化的物理模型。
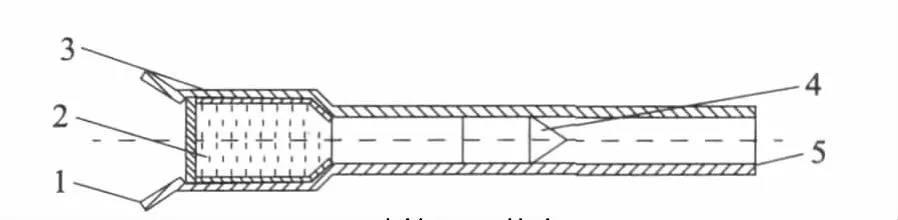
圖1 火炮的結(jié)構(gòu)示意圖
2 數(shù)學(xué)模型
該型炮的發(fā)射過程不同于其他火炮,由于采用半可燃藥筒,燃燒過程需考慮其對(duì)發(fā)射過程的影響。且在發(fā)射的最大膛壓時(shí)期有火藥氣體噴出,同時(shí)炮尾處增加了提高氣流噴出速度的拉瓦爾噴管,其發(fā)射過程的物理化學(xué)現(xiàn)象顯得相當(dāng)復(fù)雜。為了近似計(jì)算它的發(fā)射過程,需要對(duì)其進(jìn)行一定的假設(shè)與簡(jiǎn)化:該模型基于內(nèi)彈道零維模型,運(yùn)用經(jīng)典內(nèi)彈道理論進(jìn)行建模與計(jì)算。
2.1 半可燃藥筒燃燒模型[1]
該彈藥采用半可燃藥筒技術(shù),主要有金屬筒底、可燃藥筒、底火、主發(fā)射藥及彈丸等組成。半可燃藥筒在火藥燃燒時(shí)會(huì)連同藥筒一起燃燒。假設(shè)半可燃藥筒符合幾何燃燒定律,并由內(nèi)向外燃燒。可將半可燃藥筒裝藥當(dāng)作是一種混合裝藥,現(xiàn)將半可燃筒體簡(jiǎn)化成一圓柱體(圖2)。
則可推導(dǎo)出半可燃藥筒的形狀特征量:

其中:D0,d0分別為半可燃藥筒的外徑與內(nèi)徑;c0為半可燃藥筒的筒壁厚;c為半可燃藥筒的筒長(zhǎng)。
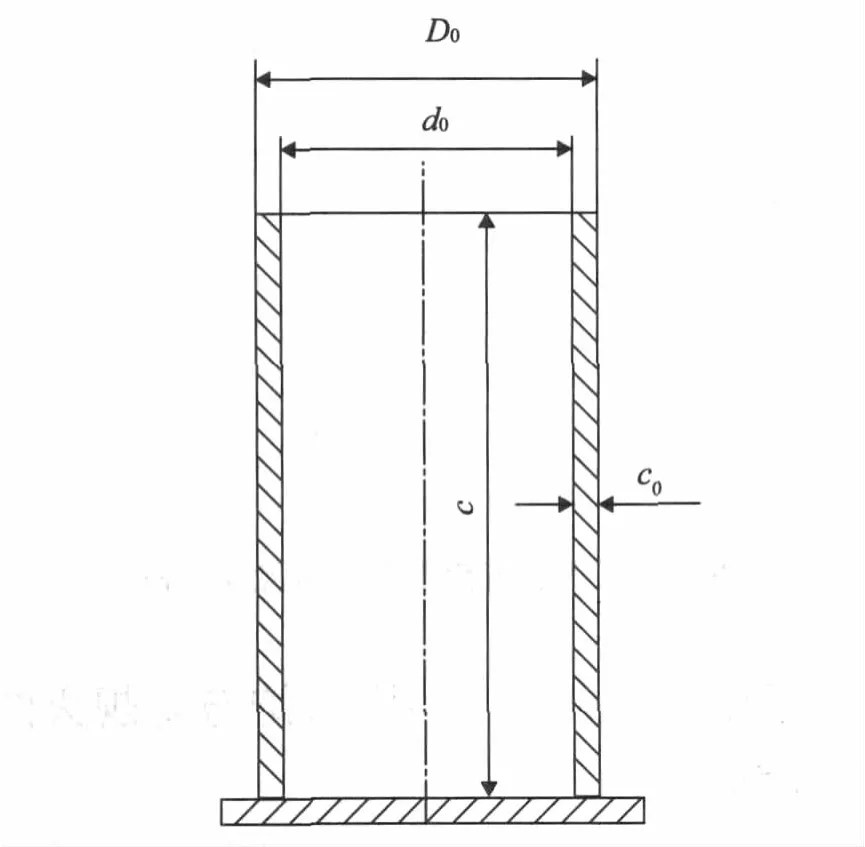
圖2 半可燃藥筒簡(jiǎn)化模型
2.2 半可燃藥筒剪切受力分析
在膛內(nèi)火藥氣體壓力的作用下,半可燃藥筒金屬筒底的受力如圖3所示。其中,pt為膛底壓強(qiáng);L為半可燃藥筒金屬筒底的厚度。
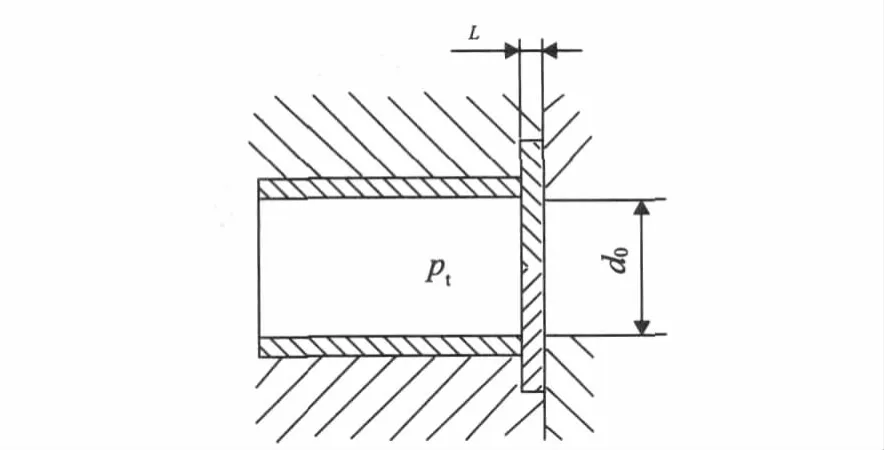
圖3 半可燃藥筒剪切受力計(jì)算簡(jiǎn)圖
在膛底壓強(qiáng)pt的作用下,金屬筒底所受到的剪應(yīng)力為:
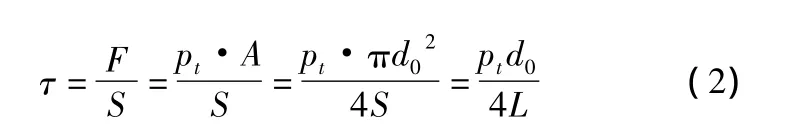
若金屬筒底所用材料的許用剪應(yīng)力為[τ],則金屬筒底被剪斷時(shí)的膛底壓強(qiáng)為:

2.3 該型火炮膛內(nèi)壓力分布假設(shè)[2]
火炮在射擊過程中有大量火藥氣體流出。氣流向兩端流動(dòng),在炮膛的某一斷面會(huì)存在一滯止點(diǎn),并假設(shè)膛內(nèi)密度均勻分布。其壓力分布為:
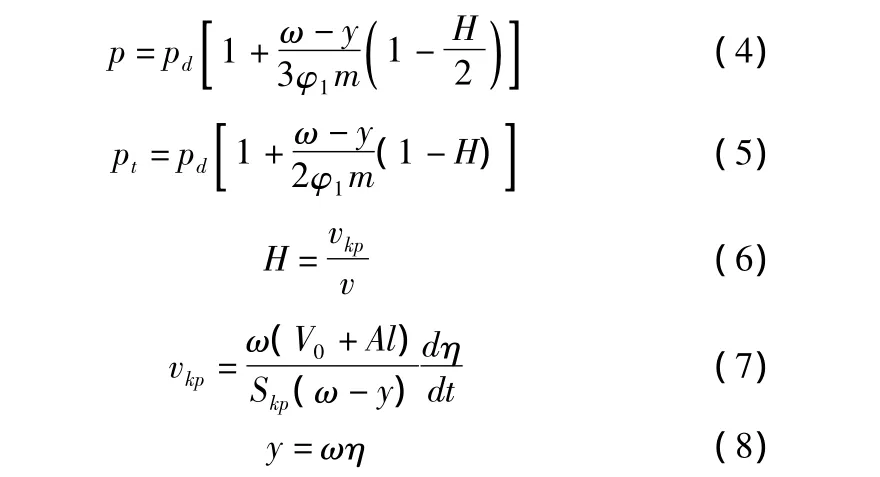
該膛內(nèi)壓力分布條件同樣適用于炮尾無火藥氣體流出的常規(guī)火炮,其中:p為膛內(nèi)平均壓力;pd為彈底壓力;ω為裝藥量;y為火藥氣體流出量;φ1為阻力系數(shù);m為彈丸質(zhì)量;H為速度比;vkp為炮尾噴管火藥氣體臨界流速;Skp為噴管臨界斷面積;η為火藥氣體相對(duì)流出量;A為炮膛斷面積。
2.4 內(nèi)彈道基本方程[2-4]
火藥形狀函數(shù):
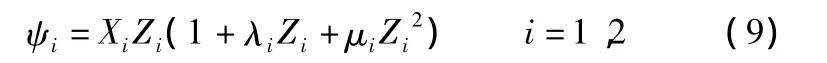
其中:ψi為火藥已燃相對(duì)質(zhì)量;Zi為火藥已燃相對(duì)厚度;Xi,λ,μi為火藥形狀特征量;i=1,2 分別表示主裝藥與半可燃藥筒。
火藥燃速方程:
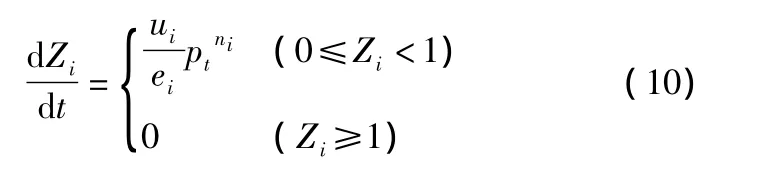
其中:ui為火藥燃速系數(shù);ni為火藥燃速指數(shù)。
彈丸速度與行程方程:
其中:l為彈丸行程;t為彈丸運(yùn)動(dòng)時(shí)間;v為彈丸速度。
彈丸運(yùn)動(dòng)方程:

其中:S為炮膛截面積。
能量守恒方程:
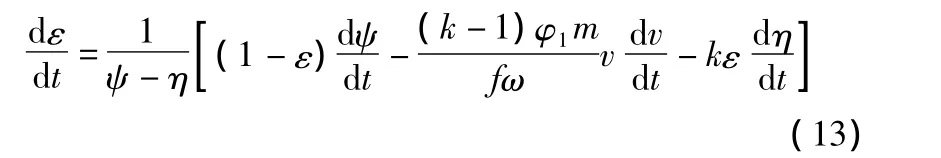
其中:ε為相對(duì)溫度;η為火藥氣體相對(duì)流量;k為絕熱指數(shù);f為火藥力。
燃?xì)鉅顟B(tài)方程:
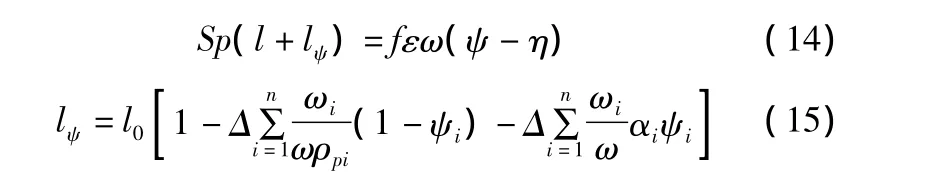
其中:lψ為藥室自由容積縮徑長(zhǎng);l0為身管長(zhǎng);Δ為裝填密度;ρpi為火藥密度;αi為氣體余容。
炮尾火藥氣體流量方程:
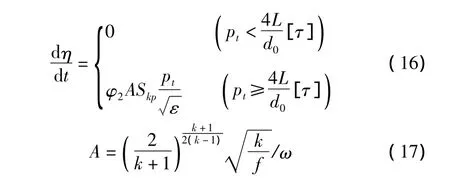
其中φ2為消耗系數(shù)。
3 數(shù)值計(jì)算與仿真結(jié)果分析
以某35 mm膨脹波火炮的參數(shù)為計(jì)算依據(jù),其具體初始計(jì)算數(shù)據(jù)可參考文獻(xiàn)[2]。半可燃藥筒金屬筒底的材料采用 H62 黃銅,其 σb=294 MPa,取[τ]=σb=98 MPa。
為檢驗(yàn)上述模型的正確與否,現(xiàn)將計(jì)算曲線與35 mm膨脹波火炮實(shí)驗(yàn)曲線作比較,從圖4可以看出,由于半可燃藥的燃燒,會(huì)導(dǎo)致最高膛壓相比會(huì)大點(diǎn),模型基本滿足要求,所以上述模型能用于實(shí)際計(jì)算。
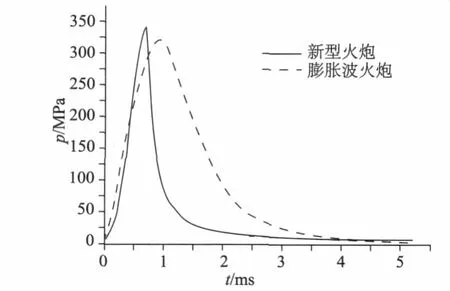
圖4 與膨脹波火炮的膛壓—時(shí)間對(duì)比曲線
3.1 半可燃藥筒金屬筒底厚度對(duì)發(fā)射性能的影響
根據(jù)上述數(shù)學(xué)模型,通過Matlab編程進(jìn)行數(shù)值計(jì)算,可以得到相關(guān)的內(nèi)彈道數(shù)據(jù)。圖5是不同的半可燃藥筒金屬筒底厚度計(jì)算出的彈丸速度曲線。
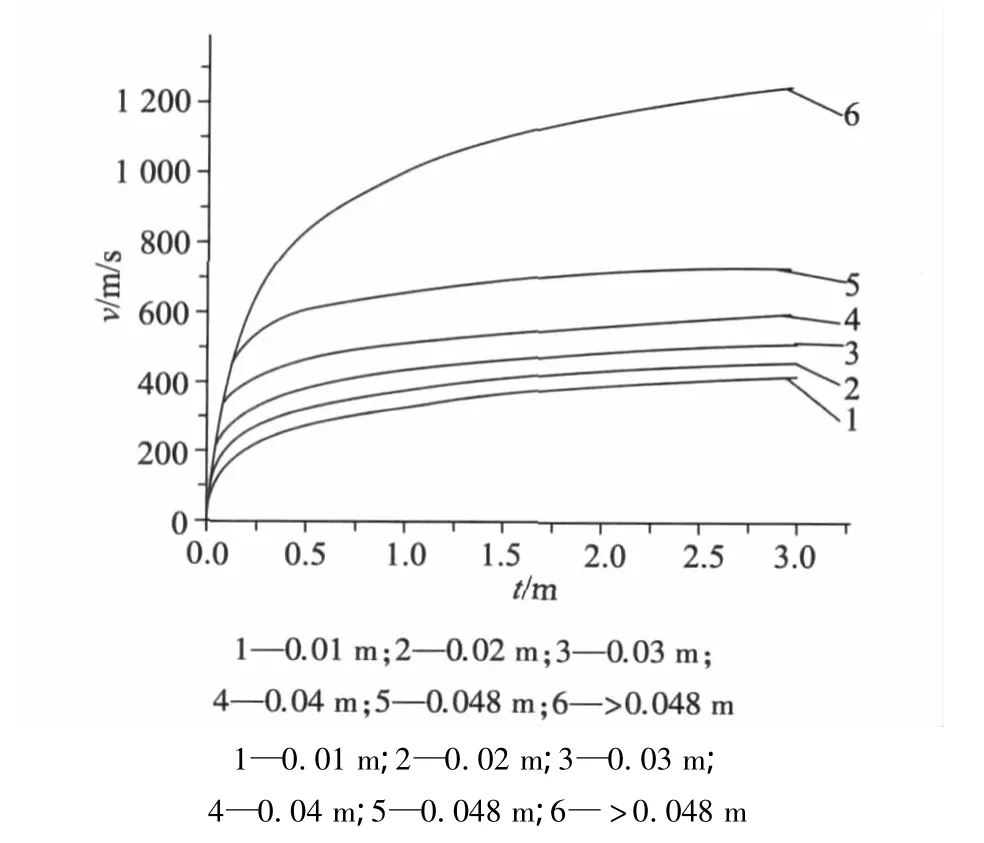
圖5 不同金屬筒底厚度下的彈丸速度—行程曲線
從圖5可以看出,隨著金屬筒底厚度的增加,彈丸初速相應(yīng)增加,但當(dāng)達(dá)到一定的值時(shí)不再變化,這是由于金屬筒底厚度的增加必然會(huì)導(dǎo)致剪斷壓強(qiáng)的增加,即火藥氣體噴出時(shí)間向后的延遲,這樣進(jìn)一步增大彈丸的初速。當(dāng)厚度達(dá)到一定程度時(shí),半可燃藥筒金屬筒底不被剪斷,其過程與閉膛火炮一樣,無火藥氣體的噴出,故發(fā)射性能不再變化。圖6是不同的金屬筒底厚度與彈丸速度的大致關(guān)系。
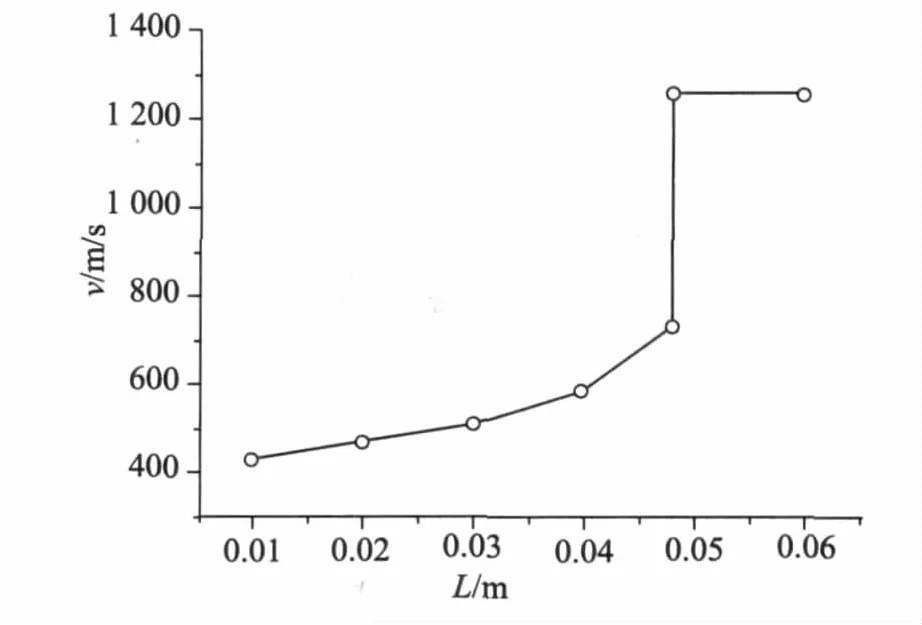
圖6 彈丸初速與金屬筒底厚度關(guān)系圖
3.2 最佳剪斷條件下該型火炮與常規(guī)火炮性能比較
為了獲得在剪斷條件下的最大彈丸初速,必須盡量使金屬筒底的厚度剛好滿足在閉膛下的最大膛壓,此時(shí)剛好被剪斷,該新型火炮獲得最大彈丸初速,達(dá)到最佳剪斷條件。
圖7是最佳剪斷條件下該型火炮與同口徑閉膛火炮的膛壓曲線,由于在火藥氣體未噴出前,該新型火炮的發(fā)射過程與常規(guī)火炮一樣,其膛壓曲線重合。當(dāng)達(dá)到最大膛壓341.01 MPa時(shí),即在內(nèi)彈道時(shí)間 0.68 ms,火藥氣體向后噴出,膛內(nèi)壓力急劇下降。這比較符合實(shí)際情況。
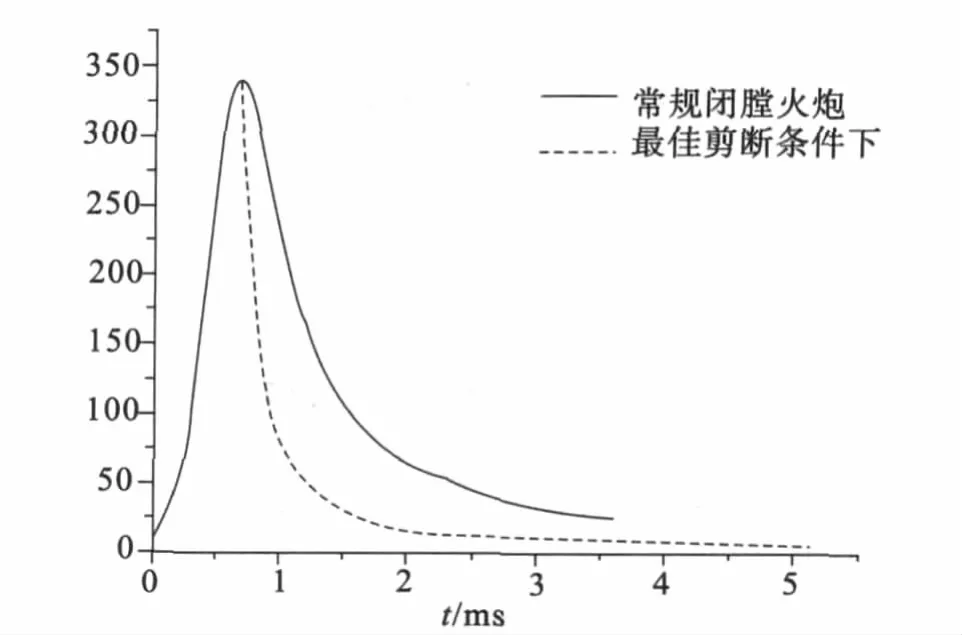
圖7 與常規(guī)閉膛火炮的膛壓—時(shí)間對(duì)比曲線
圖8是在該條件下與常規(guī)火炮的彈丸速度與行程關(guān)系的對(duì)比曲線,由于火藥氣體在最大膛壓時(shí)噴出,膛內(nèi)壓力下降,彈丸在膛內(nèi)相比閉膛火炮沒有得到足夠的加速,因此彈丸的初速要比閉膛火炮小。
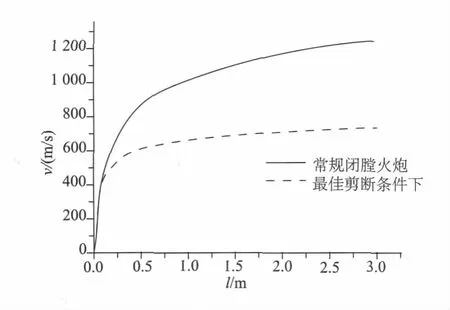
圖8 與常規(guī)火炮的彈丸速度-行程對(duì)比曲線
根據(jù)膛內(nèi)壓強(qiáng)可以計(jì)算出火藥氣體在炮膛軸線上的作用力,在炮膛閉合時(shí)的火藥氣體作用力為F=p·A,當(dāng)火藥氣體噴出時(shí)的作用力為火藥氣體對(duì)噴管的推力F=-ξ·Skp·p,其中ξ為推力系數(shù)。
圖9是該條件下與常規(guī)閉膛火炮的火藥氣體作用力的對(duì)比曲線。圖中雖然火藥氣體在炮膛軸線方向的最大力沒有發(fā)生改變,但在火藥氣體噴出后,火藥氣體作用力的方向反向,這對(duì)于反后坐裝置的設(shè)計(jì)能帶來極大的好處。
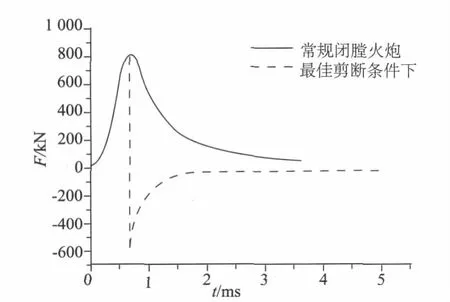
圖9 與常規(guī)閉膛火炮的火藥氣體作用力-時(shí)間對(duì)比曲線
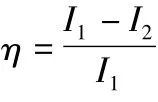
4 結(jié)語
該型火炮雖然犧牲了部分的彈丸初速,但是極大地減小了火炮發(fā)射過程中火藥氣體的作用沖量,對(duì)于不同要求的火炮武器系統(tǒng)具有重大意義。本文主要建立了它的發(fā)射模型,并以某35 mm口徑炮作為原型進(jìn)行了數(shù)值仿真。對(duì)于該型火炮的進(jìn)一步研究與工程實(shí)際應(yīng)用具有參考作用。
[1]張才友.全可燃藥筒高速發(fā)射內(nèi)彈道性能仿真[D].南京:南京理工大學(xué),2008.
[2]金志明.槍炮內(nèi)彈道學(xué)[M].北京:北京理工大學(xué)出版社,2004.
[3]王穎澤,張小兵,袁亞雄.膨脹波火炮后噴裝置流場(chǎng)性能分析[J].兵工學(xué)報(bào),2009,30(5):525-530.
[4]KATHE E.Sonic rarefaction wave recoilless gun system [P].US.Patent:6460446B1,2002-10-08.
[5]DILLON R,KATHE E.Sonic rarefaction wave low recoil gun[R].AIAA2001-0743,2001.
[6]支建莊,鄭堅(jiān),狄長(zhǎng)春,等.慣性炮尾式膨脹波火炮膨脹波速度和行程計(jì)算仿真[J].火炮發(fā)射與控制學(xué)報(bào),2009(1):5-8.
[7]張帆,廖振強(qiáng),劉國(guó)鑫,等.膨脹波槍炮發(fā)射性能若干影響因素的研究[J].兵工學(xué)報(bào),2008,29(1):23-27.

