潛孔鉆機鉆桿有限元屈曲分析和靈敏度的研究

邵 堃，袁世先

(河南職業技術學院 機電工程系，鄭州 450046)

0 引言

潛孔鉆多用于工程爆破，在巖石上鉆孔，然后將炸藥放入孔內，潛孔鉆在工作過程中承受著交變的沖擊載荷，需要根據實際情況對鉆桿的壁厚、鉆桿長度和工作時所受軸壓力來確定，這就對鉆桿提出了較高的要求，需要在滿足足夠的強度和剛度前提下還要具備穩定性，才能保證在工作過程中不會發生失穩現象，故需要對潛孔鉆的鉆桿在具體工況下進行屈曲分析，得到該鉆桿在此工況下能否滿足要求，并選取對鉆桿穩定性影響較大的參數進行靈敏度分析，有助于對設計鉆桿的主要參數進行優化的選擇，最終做到最優設計[1]。

1 潛孔鉆桿的屈曲分析

在線性屈曲分析中，是以特征值作為研究對象的，特征值是理想線性結構的理論屈服強度。進行屈曲分析的目的是為了尋找分歧點，對于線性結構，其方程為：

進行屈曲分析之前需要首先執行一個靜力分析，在靜力分析基礎上計算出應力剛度矩陣，進而求出屈曲載荷因子 ，和屈曲模態 。潛孔鉆桿在進行靜力分析時，在建模中定義了兩個參數，P1為鉆桿壁厚，P2為鉆桿長度，初始參數值P1=70mm，P2=8000mm。圖1為潛孔鉆桿的靜力分析前處理。

圖1 經歷分析前處理

圖2 耦合計算的設置

鉆桿一端施加固定約束，另外一端施加軸壓力P，將軸壓力P設置為參數，P初始值為150kN。在網格的劃分上選取掃掠方法，單元形狀為六面體。執行完靜力分析之后需將靜力學分析的結果傳遞到屈曲分析中，即靜力分析和屈曲分析相耦合，圖2為靜力分析和屈曲分析耦合計算的設置，通過Workbench的耦合功能，可以將靜力學分析中的數據傳輸到屈曲分析中，從而實現了數據的共享[5]。

在潛孔鉆桿的屈曲分析中，只選擇求前四階的屈曲載荷因子，通過計算得出鉆桿的六個屈服載荷因子。圖3為鉆桿屈曲分析的結果云圖。

計算結果中的屈曲因子為3.4 8，可知在250KN·3.48的軸壓力下，鉆桿會發生失穩現象。在潛孔鉆機工作時，軸壓力必須控制在該數值以下。從結果可以看出，只有前兩階屈服因子滿足工程實際要求。

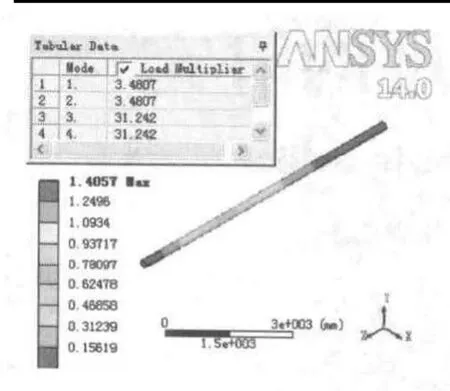
圖3 屈曲分析結果

圖4 靈敏度分析參數設置

2 潛孔鉆桿的靈敏度分析

Workbench中的Design Exp lorer主要是幫助設計人員在產品設計和使用之前確定那些不確定因素對產品零件的力學性能的影響，而且能確定如何才能最好地提高產品的可靠性，在Workbench中這些任務是利用響應面來完成的[6,7]。

Design Exp lo rer中靈敏度分析是通過響應面或者線來完成的，其支持的方法是實驗數據法。在靈敏度分析中選取的參數如下：1）P1為潛孔鉆桿的壁厚，P1初始值為70m m，變化范圍從70mm～80mm；2）P2為潛孔鉆桿的長度，P2初始值為8000mm，變化范圍從8000mm～10000mm；3）P3為潛孔鉆桿在工作過程中所受軸壓力，P3初始值為250kN，變化范圍從250kN～400kN；4）P4為潛孔鉆桿一階模態下的屈曲載荷因子，靈敏度分析主要研究參數P1、P2、P3對屈曲載荷因子P4的影響。將設置的參數傳輸到Design Exp lorer中，設置完成之后保存數據，然后進行靈敏度分析運算，圖4為靈敏度分析中各參數的設置[8]。

3 靈敏度運算結果分析

靈敏度分析完成之后，可以通過響應面或者線查看各參數對屈曲載荷因子的影響，為了找出對屈曲載荷因子影響較大的參數，可以通過查看局部靈敏度，找出各參數對屈曲載荷因子影響的程度。圖5為各參數對屈曲載荷因子影響程度。

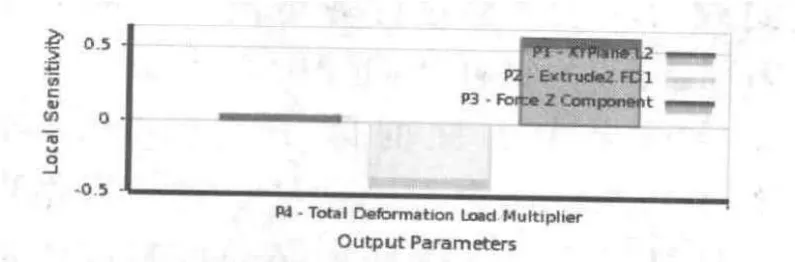
圖5 各參數對屈曲載荷因子的影響程度

圖中紅色、黃綠色和藍色分別代表P1、P2和P3對屈曲載荷因子的影響，可以看出影響屈曲載荷因子程度較大的參數為潛孔鉆桿長度P2和潛孔鉆桿所受軸壓力P3。

靈敏度分析完成之后，將鉆桿長度設置為橫坐標，屈曲載荷因子設置為縱坐標，便可以得到為潛孔鉆桿長度P2和屈曲載荷因子P4的變化關系曲線如圖6所示。

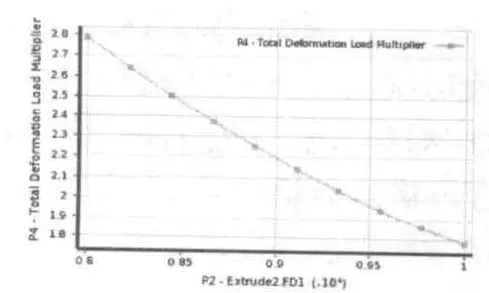
圖6 P2和P4關系曲線

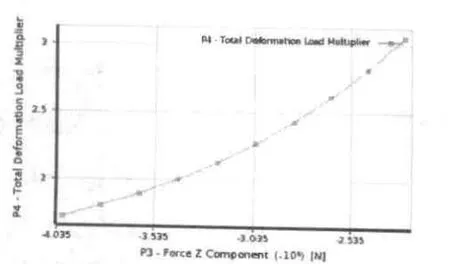
圖7 P3、P4關系曲線

隨著鉆桿長度的增加，屈曲載荷因子在減小，鉆桿穩定性變弱。可以根據實際工況在該曲線上選擇合適的點來滿足工作要求，可以在加長鉆桿的情況下，鉆桿穩定性依然能滿足要求。圖7為潛孔鉆桿所受軸壓力P3和屈曲載荷因子P4變化關系曲線。

從上圖可知隨著軸壓力的增加，屈曲載荷因子在降低。可以根據該曲線，選擇合適的點鉆桿在軸壓力增大前提下，仍然滿足穩定性要求，提高鉆孔效率。圖8為潛孔鉆桿長度P2、潛孔鉆桿所受軸壓力P3和和屈曲載荷因子P4的響應曲面。

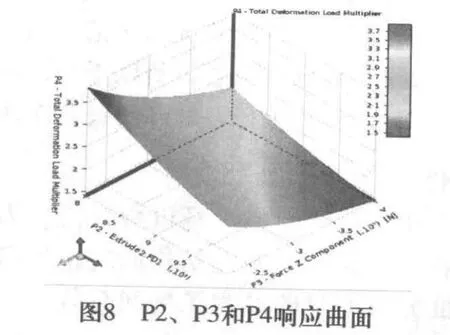
圖8 P2、P3和P4響應曲面

在潛孔鉆桿各參數綜合選擇上，可以在該曲面上尋求一點，使鉆孔深度，工作效率和穩定性都滿足要求的最優解，實現鉆桿在具體工況之下的優化設計。圖9為靈敏度分析的響應點。

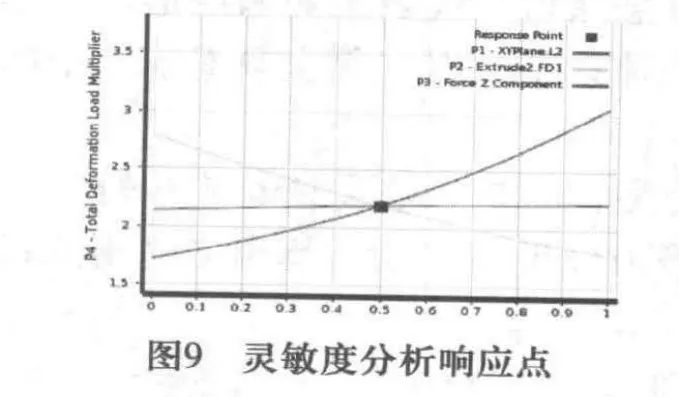
圖9 靈敏度分析響應點

在該點各參數的值對屈曲載荷因子P4的影響程度是一樣的。從圖中還可得知，達到該點數值時，各參數的具體數值，在實際情況下可以選取一個合適的屈服載荷因子，查看各參數達到該點的數值。

4 結論

通過屈曲分析可知現有的潛孔鉆桿的極限工作狀態，避免在工作過程中發生屈曲；通過靈敏度分析出來的各曲線關系，可以根據實際工況對鉆桿的長度和軸壓力進行調整，在滿足穩定性的要求下找出符合該工況的最佳參數。

[1] 吳雙斌,趙宏強,郭艷,等.潛孔鉆機鉆臂虛擬樣機建模與動力學仿真[J].計算機仿真,2012,29(1):285-288.

[2] 袁夢,劉萍,姚錄錄,等.基于靈敏度分析的無極繩連續牽引車傳動系統的可靠性優化設計[J].煤礦機械,2011(3):21-23.

[3] 石前列,吳向東,武友德.基于有限元的落地鏜銑床滑枕結構設計[J].機械設計與制造,2012(4):19-21.

[4] 歐陽炎,王棟.結構支撐位置改變時固有頻率的快速計算[J].振動與沖擊,2012,31(18):1-4.

[5] 孫蓓蓓,孫慶鴻,許志華.非線性變剛度橡膠懸架結構靈敏度分析與參數優化[J].制造業自動化,2006,28(2):1-4.

[6] 楊秀建,康南,李西濤.半掛汽車列車橫向失穩的非線性動力學機制[J].機械工程學報,2012,48(8):79-89.

[7] 戴雪芬.基于Pro/E的裝載機工作裝置動臂的有限元分析及優化設計[J].工礦自動化,2010(4):50-52.

[8] 張江濤,徐曉峰,鄭昱.基于W o rkb en ch平臺的超超臨界鍋爐給水泵轉子動力學有限元分析[J].水泵技術,2012,(2):23-27.