飛輪姿控微小衛星控制方法研究＊

李華山 閆 野 任 利

（1.防空兵學院 鄭州 450052）（2.國防科技大學航天與材料工程學院 長沙 410073）

1 引言

隨著航天技術的發展，對小衛星姿態控制系統的穩態精度和響應速度要求越來越高，且對控制算法的復雜度、抗干擾性及魯棒性有特殊要求［1］。傳統控制方法是先將姿態動力學方程簡化成俯仰通道和偏航－滾動通道，對前者單獨控制，對后者進行解耦控制。目前，對航天器姿態控制方法多采用“優化方法＋PID控制器”組合的形式，通過優化方法整定控制器參數［2～5］，文獻［6］使用 Matlab中的非線性控制設計模塊實現對PD姿態控制器的參數優化，文獻［7～8］分別使用遺傳算法和神經元算法實現PID控制器參數調整。以上方法雖能實現對航天器姿態的精確控制，但方法較復雜，且不易滿足星載小型計算機實時處理的要求。本文不考慮采用優化方法，以反作用飛輪作為控制機構，基于改進的PD控制器，對姿態耦合系統控制方法展開研究。

2 動力學方程

設沿星體的三慣量主軸各安裝一個反作用飛輪，三飛輪的質心重合于星體質心。小衛星的運行軌道為低軌近圓軌道，不考慮太陽帆板擾動，由動量矩定理得到小衛星的姿態動力學方程為

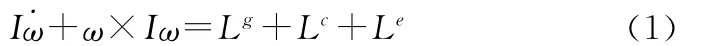
式中：I為星體的總慣量張量，且I＝diag［IxIyIz］；ω為星體角速度；Lg，Lc，Le分別為引力梯度力矩、飛輪轉軸上電機的控制力矩和外力矩。

考慮到引力梯度矩Lg的表示式為

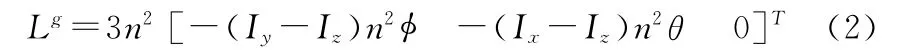
聯立式（1）、（2），進行線性化得

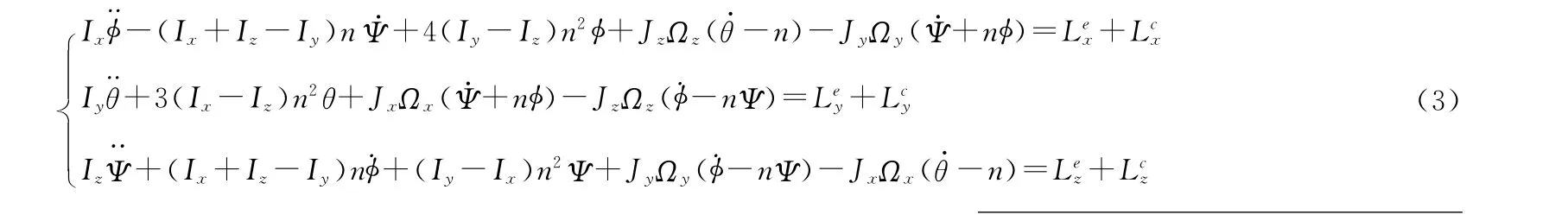
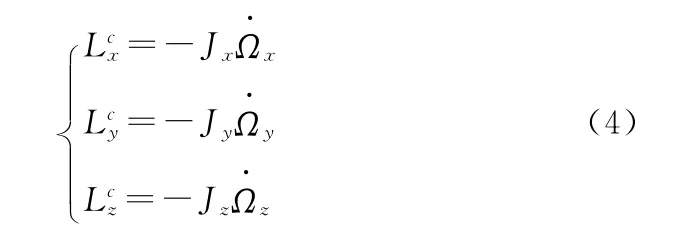
式中：φ，θ，Ψ分別為星體的滾動角、俯仰角與偏航角；n為衛星沿軌道轉動角速度；Ωx，Ωy，Ωz為飛輪相對于星體的角速度；Jx，Jy，Jz分別為三飛輪的軸向轉動慣量［9］。

由以上可得，衛星的姿態動力學方程是一個三輸入三輸出系統，且姿態的俯仰、偏航和滾動三通道相互耦合。通過解耦實現對衛星姿態的控制比較復雜，且不能滿足星載計算機實時處理的要求。

3 控制器設計

3.1 PD控制器及改進

PD控制器具有原理簡單，使用方便，適應性強，魯棒性強等優點，是一種普遍的控制規律［11］。基本的PD控制規律可描述為

式中：Kp為比例系數，Kd為微分系數，兩者都是可調的參數。增大比例系數，系統的響應速度加快，系統的超調也增加，調節時間也增長；增大微分時間常數，系統的超調量減小，穩定性提高，上升時間減小，快速性提高。

控制器參數整定多采用現代優化算法，計算過程復雜，效率低，通過設計的期望目標函數代替星體姿態角及角速度目標值的方法，可實現穩定控制器輸入量，增強控制器參數的適用性，避開參數優化過程。期望目標姿態角函數的設置基于初始姿態角、目標姿態角和期望姿態調整時間三個因素建立。以俯仰角θ為例，期望目標函數設置為

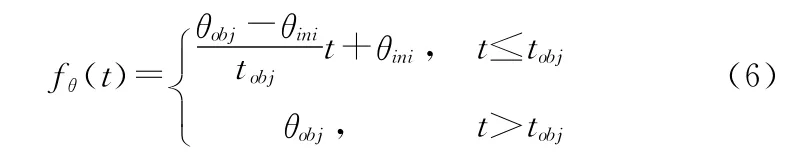
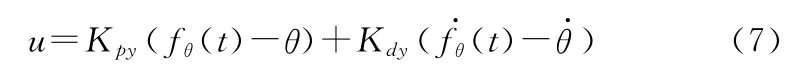
式中：θini為星體初始俯仰角，θobj為星體俯仰角目標值，tobj為期望調整時間。改進后的俯仰通道控制律描述為式中：Kpy為俯仰通道比例系數，Kdy為俯仰通道微分系數，fθ（t）、（t）分別為俯仰角及角速度的目標函數，u為控制器輸出量。圖1所示為改進的PD控制器結構圖。

3.2 姿控系統結構

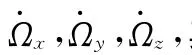
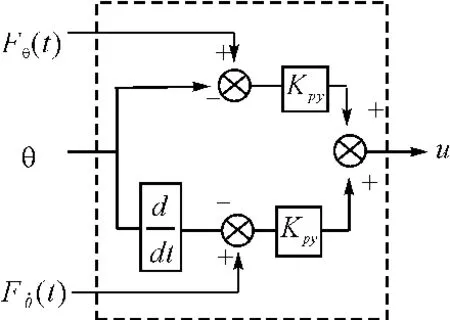
圖1 改進的PD控制器結構

4 仿真分析

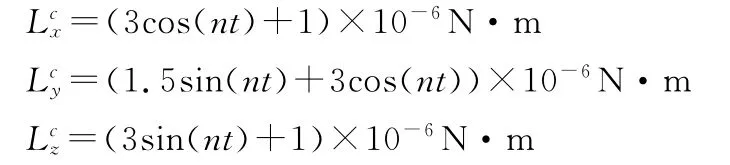
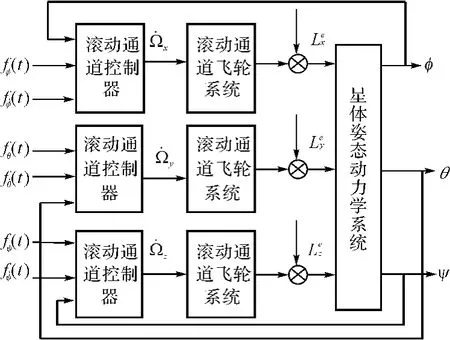
圖2 控制系統結構圖

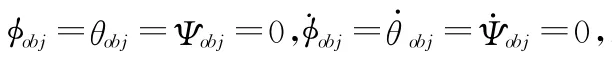
圖3 姿態角響應

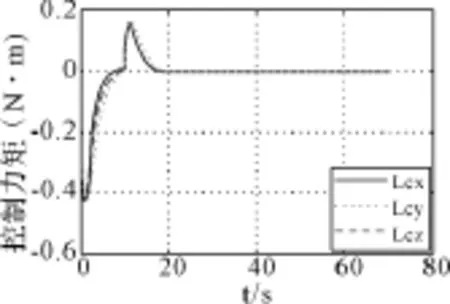
圖4 控制力矩

在實際空間環境中，干擾力矩無法精確預知，其幅值可能在可在一定范圍內波動。將干擾幅值提高一個量級，即時，其姿態角的響應如圖5所示。與圖3相比，其響應過程變化微小，系統穩態精度保持不變，控制效果明顯。

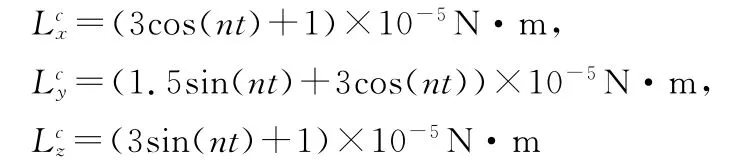
考慮飛輪系統電機性能等影響，認為飛輪實際輸出的控制力矩是理想控制力矩的85%，即

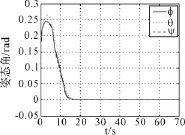
圖5 干擾變化后的姿態角響應

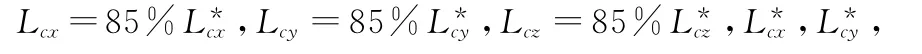
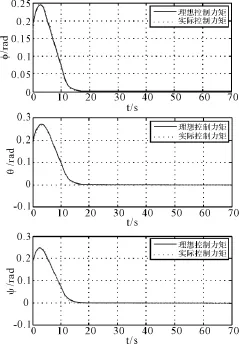
圖6 實際控制力矩下的姿態角響應

5 結語

本文通過設計期望目標函數的方法，將姿態角及角速度目標值設置為期望目標函數的形式，其與實際姿態角及角速度的偏差作為控制器的輸入、飛輪轉動角加速度作為輸出，不考慮解耦控制，在每個通道分別加入控制器。仿真結果證明：控制系統在保證姿態響應過程有良好的快速性及較高的穩態精度基礎上，且對環境干擾變化及星體內部不確定性具有良好的適應性。在實際應用中可直接通過星載計算機生成期望目標函數，簡單高效。穩態響應時間與理想調整時間有一定延遲，但滿足工程指標。

［1］劉昆，劉述田，等.微小衛星反作用飛輪控制方法研究［J］.上海航天，2004，21（2）：11－13.

［2］王偉，張晶濤，柴天佑.PID參數先進整定方法綜述［J］.自動化學報，2000，26（3）：347－355.

［3］Astrom K J，Hagglund T，Wallenborg A.Automatic Tuning of digital Controllers with applications to HVAC plants［J］.Automation，1993，29（5）：1333－1343.

［4］Astrom K J，Hagglund T，Hang C C，Ho W K.Automatic Tuning and adaptation for PID Controllers－A survey ［J］.Control Eng.Pratice，1993，1（4）：699－714.

［5］Schei T S.Automatic tuning of PID controllers based on transfer function estimation［J］.Automatica，1994，30（12）：1983－1989.

［6］周黎妮，唐國金.基于Matlab／Simulink的航天器姿態動力學與控制仿真框架［J］.系統仿真學報，2005，17（10）：2517－2520.

［7］李源，吳宏悅.基于遺傳算法PID整定的衛星姿態控制研究［J］.中國空間科學技術，2007（4）：66－71.

［8］劉軍，韓湘.基于單神經元的衛星姿態自適應PID控制［J］.計算機仿真，2006，23（3）：45－48.

［9］黃釧圭.航天器姿態動力學［M］.長沙：國防科技大學出版社，1997.

［10］白洪瑞，呂強，劉峰，等.基于UM6慣導模塊的四旋翼飛行器姿態控制［J］.計算機與數字工程，2012（8）.

［11］劉金琨.先進PID控制 Matlab仿真［M］.第二版.北京：電子工業出版社，2006.