無人機傾斜轉(zhuǎn)彎飛行控制系統(tǒng)設(shè)計與仿真＊

王凌艷 施敏良 林秋杰 蘭 甸

（中國洛陽電子裝備試驗中心 洛陽 471003）

1 引言

隨著無人機（UAV）開始向高空高速、大機動能力的發(fā)展，側(cè)滑轉(zhuǎn)彎（STT）控制方式已難以提供足夠的過載能力來滿足UAV高機動性能要求［1］。傾斜轉(zhuǎn)彎（BTT）控制方式相對（STT）控制方式在氣動效率、機動能力、控制性能等方面具有明顯優(yōu)勢［2～3］，借鑒現(xiàn)代導(dǎo)彈控制系統(tǒng)的設(shè)計思想，BTT控制方式可以解決UAV側(cè)向過載能力不足的問題，滿足吸氣式動力裝置對小側(cè)滑角的要求，是提高UAV機動性能的一項關(guān)鍵技術(shù)。

無人機既具有導(dǎo)彈的特點又有人駕駛飛機的特點，它采用面對稱的飛機平臺，其氣動外形上的不對稱性，以及BTT控制方式?jīng)Q定了它是一個具有較強運動學(xué)耦合、慣性耦合、氣動耦合和控制耦合的多變量非線性系統(tǒng)［4］。為了提高無人機的制導(dǎo)控制精度，在BTT控制律設(shè)計中必須對模型的非線性耦合給予考慮。BTT控制系統(tǒng)設(shè)計面臨的技術(shù)難點包括：1）由于UAV大包線飛行引起UAV參數(shù)大范圍急劇變化，要求控制系統(tǒng)有強魯棒性以保證UAV在整個飛行過程中始終具有優(yōu)良的靜態(tài)品質(zhì)和動態(tài)特性，從而保持其跟蹤性能在整個飛行包線范圍內(nèi)均能滿足要求［5］；2）采用BTT控制方式的 UAV是具有氣動耦合、運動耦合和控制耦合的強耦合系統(tǒng)［6～7］，耦合作用給控制系統(tǒng)設(shè)計帶來了很大的挑戰(zhàn)。

針對傾斜轉(zhuǎn)彎（BTT）UAV控制中的多變量強耦合問題，文章研究了一種適用于傾斜轉(zhuǎn)彎控制UAV的自適應(yīng)神經(jīng)網(wǎng)絡(luò)反演算法，以實現(xiàn)自動駕駛儀的解耦控制。根據(jù)BTT控制的基本特性，建立UAV的非線性控制模型，并將其轉(zhuǎn)化為適合于反演設(shè)計的塊控模型。在此模型上，基于反演的非線性控制系統(tǒng)綜合設(shè)計方法，并加入神經(jīng)網(wǎng)絡(luò)來估計不確定性，設(shè)計了自動駕駛儀控制器。

2 自適應(yīng)反演控制律設(shè)計

控制律設(shè)計的目的是保證UAV的穩(wěn)定，并達到跟蹤系統(tǒng)側(cè)向和法向指令信號的目的，此外在跟蹤過程中還需要保持側(cè)滑角為小量。本節(jié)將針對傾斜轉(zhuǎn)彎UAV系統(tǒng)設(shè)計一種自適應(yīng)反演控制律，該控制律加入在線神經(jīng)網(wǎng)絡(luò)估計不確定性，通過狀態(tài)觀測器觀測神經(jīng)網(wǎng)絡(luò)權(quán)值，采用backstepping的遞歸算法，基于Lyapunov穩(wěn)定性原理，控制系統(tǒng)跟蹤期望的軌跡。

2.1 系統(tǒng)定義與假設(shè)

考慮具有如下形式的非線性系統(tǒng)：

式中：x＝［x1x2… xn］T為狀態(tài)向量；u為實際輸入向量；y為系統(tǒng)輸出向量；Ωi為系統(tǒng)中存在的不確定性。

控制系統(tǒng)設(shè)計目標(biāo)是得到能夠跟蹤期望輸出信號的魯棒跟蹤控制器。通過自適應(yīng)反演算法設(shè)計控制器，根據(jù)反演算法對系統(tǒng)形式的要求，對系統(tǒng)可作以下假設(shè)：

1）gi（i＝1，2，…，n）有界且可逆。

2）存在未知連續(xù)函數(shù)φi（x1，x2，…，xn），i＝1，2，…，n，使得‖Ωi‖≤φi，i＝1，2，…，n。

3）RBF神經(jīng)網(wǎng)絡(luò)可以逼近任意連續(xù)函數(shù)，不確定性Ωi可寫成如下形式：

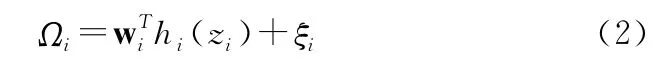
其中，

式（2）、（3）中 wi，i＝1，2…n為網(wǎng)絡(luò)權(quán)重矩陣，為區(qū)別其他列向量與標(biāo)量，使用矩陣向量形式標(biāo)記；zi為輸入向量；cij，j＝1，2…l為高斯函數(shù)中心點，sij，j＝1，2…l為高斯函數(shù)形狀參數(shù)，l為隱含層節(jié)點數(shù)；ξi為神經(jīng)網(wǎng)絡(luò)重構(gòu)誤差。

定義誤差信號e1＝x1－yr，e2＝x2－x2d，…，ei＝xixid，其中yr，xid，i＝1，…，n分別為期望的輸出與狀態(tài)量。

2.2 反演控制器解耦設(shè)計

第1步 由e1＝x1－yr，得到

將x2作為式（4）的虛擬控制，根據(jù)反演算法，選擇最優(yōu)虛擬控制量

則選取Lyapunov函數(shù)如下所示

其中

將式（10）、（13）代入式（4）得到

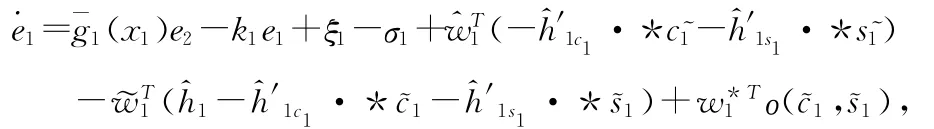
將式（6）、（10）、（11）、（12）、（13）代入式（4）得到

選擇自適應(yīng)調(diào)節(jié)律

將式（15）、（16）、（17）代入式（14），得到

有

魯棒項取為

將式（19）、（20）、（21）、（22）代入式（18）

第n步 誤差量en＝xn－xnd，對en求導(dǎo)得到

選擇最優(yōu)控制

用RBF神經(jīng)網(wǎng)絡(luò)對不確定補償，對神經(jīng)網(wǎng)絡(luò)權(quán)值和高斯函數(shù)估計得到

σn為引入的魯棒項。選取Lyapunov函數(shù)

自適應(yīng)調(diào)節(jié)律和魯棒項取為

將式（28）、（29）、（30）、（31）代入式（27）得到

其中

2.3 穩(wěn)定性分析

3 無人機傾斜轉(zhuǎn)彎控制系統(tǒng)自適應(yīng)反演設(shè)計

由于無人機（UAV）通常為面對稱布局，因此在側(cè)滑和滾動通道間存在與攻角密切相關(guān)的強耦合，此外滾動和偏航通道也存在較強的控制耦合。這種非軸對稱的氣動布局和特殊的控制方式，使得通常的線性解耦假設(shè)會導(dǎo)致較大的模型失真，因此需要建立考慮耦合因素的UAV非線性模型。

3.1 BTT控制UAV系統(tǒng)反饋模型

為了設(shè)計控制律，需要建立BTT控制UAV系統(tǒng)模型。在不考慮地球自轉(zhuǎn)及機體氣動變形的情況下，基于彈體坐標(biāo)系，在文獻［8］所給定氣動參數(shù)的條件下，UAV飛行的動力學(xué)方程可以表示為

由此模型可以看出，在俯仰、偏航、滾轉(zhuǎn)三通道存在明顯的交叉耦合，是一個非線性強耦合的復(fù)雜多變量系統(tǒng)。tan（β）pcos（α）、psin（α）分別是俯仰，偏航通道中的運動耦合，qr、pq、pr分別為滾轉(zhuǎn)、俯仰、偏航三通道間的慣性耦合。這些耦合項隨滾轉(zhuǎn)角速率p的增大而增大。在BTT控制無人機飛行過程中，由于滾動通道起主要控制作用，p的數(shù)值較大，因此在控制律設(shè)計過程中不能忽略由于滾動帶來的控制耦合問題。

反演設(shè)計是一種基于Lyapunov方法的控制系統(tǒng)設(shè)計技術(shù)，能夠適用于嚴(yán)格反饋系統(tǒng)或塊反饋系統(tǒng)。為了便于利用反演設(shè)計控制律，并實現(xiàn)控制解耦，根據(jù)塊控原理［9，11］，在不考慮地球自轉(zhuǎn)及UAV機體氣動變形的情況下，UAV的非線性控制模型可以改寫成狀態(tài)反饋塊模型：

其 中，x1＝ ［αβφ］T，x2＝ ［p q r］T，u＝ ［δpδqδr］T，y＝［nynz］T。Ω1、Ω2為由于氣動參數(shù)隨時間變化、外部擾動、噪聲引起的不確定項。

3.2 BTT控制UAV系統(tǒng)自適應(yīng)反演設(shè)計

針對BTT控制UAV系統(tǒng)模型，通過神經(jīng)網(wǎng)絡(luò)自適應(yīng)反演算法得到第一個虛擬控制

根據(jù)所推導(dǎo)RBF神經(jīng)網(wǎng)絡(luò)自適應(yīng)反演算法取自適應(yīng)調(diào)節(jié)律和魯棒項

對式（37）取實際控制

自適應(yīng)調(diào)節(jié)律和魯棒項

4 仿真結(jié)果

在UAV傾斜控制系統(tǒng)模型上進行仿真，對于面對稱布局的UAV，通常采用BTT－90控制方式，因此，傾斜控制系統(tǒng)調(diào)試參數(shù)時選取幅值為90°的階躍輸入作為傾斜角輸入指令。

圖1 指令信號為正弦波信號時跟蹤曲線

選擇控制器參數(shù)k1＝25，k2＝20，Γc1＝Γc2＝0.1，λw1＝λw2＝0.047，λs1＝λs2＝0.025，λc1＝λc2＝0.6。圖1為指令信號為正弦信號時，在無擾動的情況下，側(cè)滑角、攻角、側(cè)向和法向過載跟蹤指令信號曲線圖。圖2、3、4分別為參數(shù)攝動條件下滾轉(zhuǎn)角、法向過載跟蹤曲線，其中實線和點線分別為指令曲線和無參數(shù)攝動條件下跟蹤曲線，點劃線和虛線分別為Clδp向上和向下攝動20%時的跟蹤曲線。圖5為側(cè)滑角控制圖。

圖2 參數(shù)攝動條件下滾轉(zhuǎn)角跟蹤曲線

圖3 指令信號為方波信號時參數(shù)攝動條件下滾轉(zhuǎn)角跟蹤曲線

圖4 指令信號為正弦波信號時參數(shù)攝動條件下滾轉(zhuǎn)角跟蹤曲線

圖5 指令信號為方波信號時側(cè)滑角控制圖

由圖1可以看出，在不存在參數(shù)擾動的條件下，所設(shè)計的UAV飛行控制系統(tǒng)能夠在保持側(cè)滑角和法向過載為小量的同時較好跟蹤滾轉(zhuǎn)角和側(cè)向過載指令；由圖2、3、4、5可以看出所設(shè)計的系統(tǒng)在參數(shù)擾動條件下，仍然能夠很好的跟蹤滾轉(zhuǎn)角和側(cè)向過載指令，同時保持側(cè)滑角為小量，這證明該系統(tǒng)具有較好的魯棒性和自適應(yīng)性。

5 結(jié)語

在建立無人機傾斜轉(zhuǎn)彎控制反饋塊模型的基礎(chǔ)上，通過加入自適應(yīng)神經(jīng)網(wǎng)絡(luò)的反演算法設(shè)計了無人機傾斜轉(zhuǎn)彎飛行控制系統(tǒng)。仿真結(jié)果顯示該控制器能夠?qū)崿F(xiàn)控制解耦目的，且對指令信號跟蹤效果良好，表明了加入自適應(yīng)反演算法設(shè)計無人機傾斜轉(zhuǎn)彎飛行控制系統(tǒng)的可行性和有效性。

［1］李怡勇.無人機非線性飛行控制方法研究［D］.北京：裝備指揮技術(shù)學(xué)院，2005：4－6.

［2］R.T.Reichert.Homing Performance Comparison of Selected Airframe Configurations Using Skid－to－Turn and Bank－to－Turn Steering Policies［R］.National Aeronautics and Space Administration，1981：723－725.

［3］Frederick W.Riedel.Bank－To－Turn Control Technology Survey for Homing Missiles［R］.National Aeronautics and Space Administration，NASA Contractor Report，1980：123－130.

［4］鄭建華，楊滌.魯棒控制理論在傾斜轉(zhuǎn)彎導(dǎo)彈中的應(yīng)用［M］.北京：國防工業(yè)出版社，2001：12－13.

［5］陳欣，楊一棟，張民.一種無人機姿態(tài)智能PID控制研究［J］.南京航空航天大學(xué)學(xué)報，2003，35（6）：23－24.

［6］江燕俊，周軍，林鵬.高超音速BTT巡航飛行器變結(jié)構(gòu)控制系統(tǒng)設(shè)計［J］.計算機仿真，2009，26（12）：73－76.

［7］李揚，陳萬春.高超聲速飛行器BTT非線性控制器設(shè)計與仿真［J］.北京航空航天大學(xué)學(xué)報，2006，32（3）：30－33.

［8］Schumacher，Darren Andrew，PH.D.Tactical missile autopilot design using nonlinear control［D］.America：The university of Michigan，1994：87－89.

［9］Vadim I Utkin，De Shiou Chen，Hao Chi Chang.Block control principle for mechanical systems［J］.Journal of Dynamic Systems measurement and Control，2000，122（1）：1－10.

［10］呂強，郭善亮，王冬來，等.基于DSP四旋翼飛行器姿態(tài)控制系統(tǒng)硬件設(shè)計［J］.計算機與數(shù)字工程，2011（7）.

［11］胡云安，晉玉強，查旭.BTT導(dǎo)彈塊模型的魯棒自適應(yīng)設(shè)計［J］.宇航學(xué)報，2004，25（2）：225－229.