一種基于分層分析算法的實時最優(yōu)消防應急救援路徑算法

●李超鵬

(太原市消防支隊，山西太原 030024)

隨著我國社會經濟的快速發(fā)展，城市規(guī)模迅速擴大，各類型火災發(fā)生頻率逐漸增大，這直接威脅人民群眾的生命財產安全。消防救援作為社會的保障力量，能否及時到達火災發(fā)生地點實施救援至關重要，因而救援路徑的選擇是關鍵。目前典型的消防救援路徑選擇算法是Dijkastra算法及其改進算法［1－4］，這些算法適用于距離是衡量路線優(yōu)劣惟一標準的情況，這就要求路網(wǎng)暢通度好，道路規(guī)格較高及較少的交叉路口等［5］。但是在實際的救援工作中，路網(wǎng)中不同路段的暢通度，道路規(guī)格及交叉口數(shù)量差別很大，而且路網(wǎng)是動態(tài)變化的，經常會發(fā)生由于無法預測的因素延誤應急救援力量到達被救援地點的時間，影響救援效果，造成不必要的人員傷亡或經濟損失。本文提出了一種實時的分層分析算法計算最優(yōu)路徑。該方法不僅考慮了路網(wǎng)中不同路段的暢通度、道路規(guī)格及交叉路口數(shù)量等因素，同時還充分考慮路網(wǎng)狀態(tài)實時變化，使用局部規(guī)劃技術應對突發(fā)事件，修正全局路徑，保證車輛行駛時間最短。實驗結果表明，該算法可以作為應急救援路徑選擇的依據(jù)，同時實際應用證明該算法有效可靠。

1 基于分層分析算法的消防救援路徑規(guī)劃

現(xiàn)有典型的最短路徑算法是Dijkastra算法及其改進算法，算法的基本思想是遍歷起點到終點的道路進而選擇最短的路徑。然而實際情況并非如此，如應急救援車的車重是否超過橋梁限重，應急救援車的車高是否可以穿過高架橋，應急車輛經過的道路交叉口延誤是否交叉及應急車輛通行路段是否進行交通管制等等。所以不能只考慮道路長短。使用層次分析法可以將上述情況納入考慮，得出最優(yōu)應急救援路徑。

1.1 層次分析法

人們在進行社會的、經濟的以及科學管理領域問題的系統(tǒng)分析中，面臨的常常是一個由相互關聯(lián)、相互制約的眾多因素構成的復雜而往往缺少定量數(shù)據(jù)的系統(tǒng)。層次分析法為這類問題的決策和排序提供了一種新的、簡潔而實用的建模方法。用層次分析法建模，可分為三個步驟首先建立遞階層次結構模型，其次構造出各層次中的所有判斷矩陣，最后進行一致性檢驗。

1.2 消防應急求援道路層次結構模型

本文將消防求援車輛到達救援地點時間最短作為決策目標，綜合考慮了道路規(guī)格、道路通行方向，道路行駛時間，交叉路口延誤時間作為影響決策因素，得出如下結構模型見圖1。

1.3 構造判斷矩陣

根據(jù)圖1層次結構模型以及多位專家對指標的評價意見，可得出影響道路權值因素的重要性排序，B1＞B2＞B3=B4，并構造出各層次的判斷矩陣，然后采用和法計算得到權重。對于目標O構造的各影響力因素Bi的相對重要性判斷矩陣O－B見表1。同理構造出判斷矩陣B－C的權重，排序見表2。

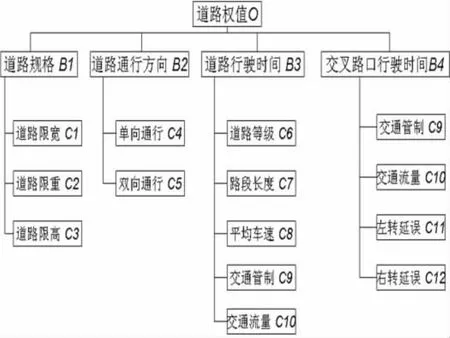
圖1 消防應急求援道路層次結構模型

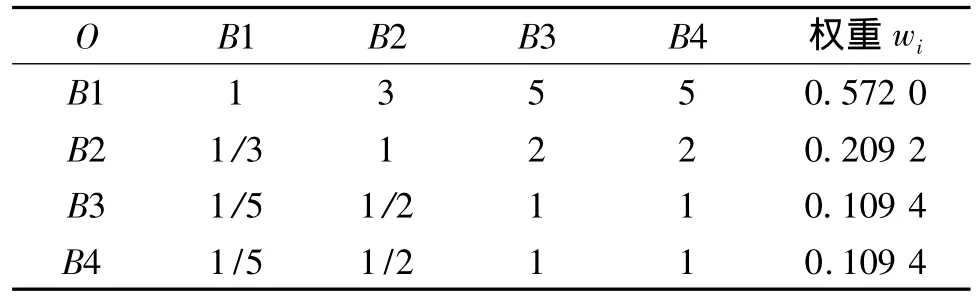
表1 相對重要性判斷矩陣O－B

表2 相對重要性判斷矩陣B－C及特征向量

以上計算結果一致性檢驗通過。上述結果表明，在所有影響應急救援行動到達被救援地點時間的因素中，道路限寬、限高、限重是需要首先考慮的因素，其次交通管制、道路通行方向以及交通流量等因素對救援車輛到達時間影響權重較大。這與實際情況相符，也從另一個角度驗證了計算結果。

1.4 無綱量化屬性數(shù)據(jù)

由于道路屬性是從不同的角度來描述道路形態(tài)，因而各個道路屬性的單位不同，例如路段車速單位是km·h－1，路段長度單位是km，而左/右轉延誤單位是min，為便于將不同屬性數(shù)據(jù)統(tǒng)一進行計算就是屬性數(shù)據(jù)的無綱量化。本文使用成本型屬性集的無綱量化標準函數(shù)進行無綱量化，對于任一屬性pi∈U，其取值范圍為［mi，Mi］，則無綱量化后屬性 ri為:

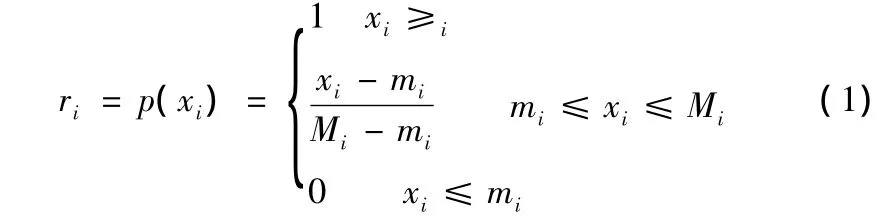
如果道路屬性 C1，C2，…，C12 對應的權值為 ω1，ω2，…，ω12，無綱量化后的對應屬性為 r1，r2，…，r12，消防應急求援時間T為:

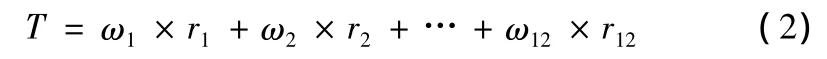
1.5 基于分層分析法的最優(yōu)路徑

從前文利用層次分析法求得的路段權值分別賦予各個路段，因而分層分析法求得最優(yōu)路徑數(shù)學模型為，將路網(wǎng)定義為一個賦權圖G(V，E)，每一邊e(vi，vj)對應權值表示為w(e)，設R是起點Vs到終點Vt所有路徑的集合，r為其中一條路徑，r∈R，路徑r的權為w(r)即w(r)=∑w(e)，目標是求得一條起點Vs到終點Vt權最小的路徑r0，即w(r0)=minw(ri)。基于分層分析法的最優(yōu)路徑算法基本流程如下:(1)車輛由起始點S向目標節(jié)點T行駛，定義集合S={Vs}，T={其余頂點}，w(Vs，Vi)＜ Vs，Vi＞ 弧上的權值。T中頂點對應的權值w(Vs，Vi);(2)從T中選取一個其權值為最小的頂點Ti，且該頂點不在S中，將Ti加入S;(3)對其余T中頂點的權值進行修改，若加進W作中間頂點，從V0到Vi的權值變小，則修改此權值。重復步驟(2)、(3)，直到S中包含所有頂點為止。

2 基于分層分析算法的實時最優(yōu)消防應急救援路徑路徑規(guī)劃

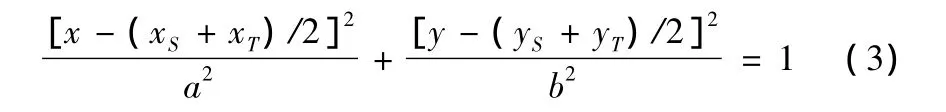
其中，x、y為橢圓任意點的坐標，xS、yS、xT、yT分別為起點S、終點T的坐標。a、b分別為橢圓長短軸。本文章橢圓的a、b值選取過程如下:(1)首先從太原市一中隊轄區(qū)電子地圖855個點中隨機選取30個點，放入集合A和B中，并計算其笛卡爾乘積C=A×B={(a，b)|(a∈A)∧(b∈B)};(2)集合C中含有900對點，求取集合C中900對點的直線距離與最短路徑比值放入集合R;(3)對集合R進行統(tǒng)計分析得出特定系數(shù)，該系數(shù)需滿足95%置信水平，且其值不大于5。本算法選取集合R中元素的算術平均值滿足該條件。經計算，集合R中元素的算術平均值該值為1.543;(4)按如下公式計算橢圓長袖2a，短軸 2b。

層次分析法是在給定路網(wǎng)結構和交通流分布信息的情況下，綜合考慮道路規(guī)格、交通管制及交通流量等因素，將路網(wǎng)抽象為不同層，提供從起點到目的地的全局最優(yōu)/最短行駛路徑。但是路網(wǎng)狀態(tài)時實時動態(tài)變化的［6］，例如突發(fā)的交通事故。該算法不能充分考慮路網(wǎng)狀態(tài)實時變化，難以應對路網(wǎng)中的突發(fā)事件，因而在車輛出行的最短路徑中需要使用局部規(guī)劃技術應對突發(fā)事件，修正全局路徑，保證救援車輛到達目的地行駛時間最短。

現(xiàn)有的局部規(guī)劃技術是通過限定搜索區(qū)域實現(xiàn)的，典型的限定搜索區(qū)域方法包括圓形法［7］、橢圓法［8］、橢圓外切矩陣［9］、橢圓內含矩陣［10］等。由于橢圓法被證明具有較高的可信度，同時橢圓區(qū)域大小依賴于統(tǒng)計經驗，由于每個消防基層中隊轄區(qū)內道路數(shù)量有限，因而具有很強的可行性。綜上兩點本文選用橢圓作為限定搜索區(qū)域。假設出行的起點為S到目標點為T，橢圓方程為:

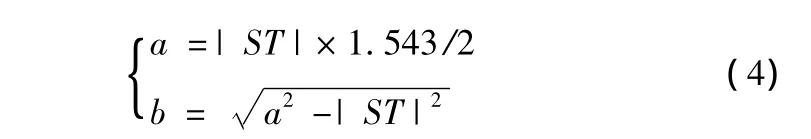
橢圓限制算法給出的置信水平95%，表明在橢圓內找不到全局最短路徑的可能行不大于5%，即使是剩下的5%不是全局最短路徑也至少是局部最短路徑，所以一般認為這5%是完全可以忽略的。在獲得了限制搜索區(qū)域的基礎上。具體的算法流程如下。

2.1 算法基本流程

步驟1:車輛沿著層次分析法得出的全局規(guī)劃路徑R，由起始點S向目標節(jié)點T行駛，直到如下中某種情況出現(xiàn):(1)到達目標節(jié)點Ti停止搜索;(2)車輛到達節(jié)點i時，路段(i，j)出現(xiàn)障礙物(如突發(fā)事件、交通堵塞，該數(shù)據(jù)來源于交通指揮系統(tǒng))，轉自步驟2。

步驟2:重置該路段(i，j)權值Wi

步驟3:在橢圓區(qū)域內(節(jié)點i作為新的起點S，目標節(jié)點T不變)重新計算替代路徑。重新計算好的替代路徑與橢圓區(qū)域外的全局規(guī)劃路徑形成新的全局路徑。

步驟4:沿著新得到的路徑前進，直到如下中某種情形出現(xiàn):(1)到達目標節(jié)點Ti停止搜索;(2)車輛到達節(jié)點i時，路段(i，j)出現(xiàn)障礙物(如突發(fā)事件、交通堵塞)，轉自步驟2。

2.2 實驗驗證及結果分析

實驗過程中本文首先使用MapInfo建立太原市一中隊轄區(qū)的消防救援電子地圖，該電子地圖主要圖層有:重要道路圖層，一般道路圖層，小路圖層，消防中隊圖層，消防安全重點單位圖層，一般單位圖層，水源分布圖層及消火栓分布圖層。

實驗假設太原市一中隊轄區(qū)內某大廈發(fā)生火災，以太原市一中隊為起點，該大廈為終點選取最優(yōu)路徑。該大廈位于師范街中段，黨校路東側，塢城中路西側，該大廈南側緊鄰居民區(qū)，且樓間距較近。該大廈共32層，1－3層是商場，4－10層為寫字樓層，10層之上為居民住宅。由于人口密度大，不易疏散，極易造成人員傷亡，需調派高空消防云梯車、搶險救援消防車和水罐消防車前往救援。消防車參數(shù)見表3。

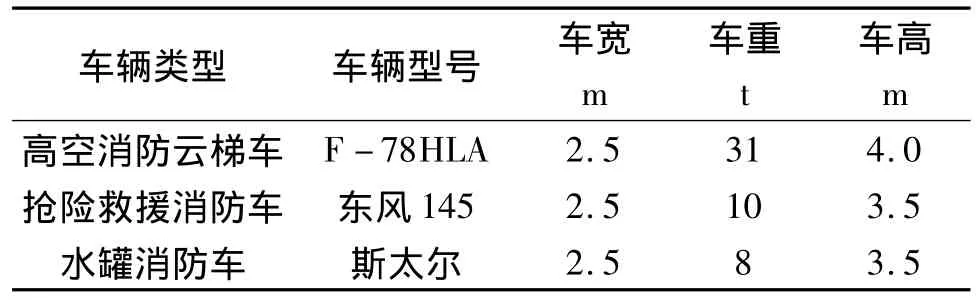
表3 消防車參數(shù)表

消防一中隊位于起火點西北部，有多條路徑可通往救援。圖2為未出現(xiàn)局部堵塞時最優(yōu)路徑方案，其中虛線路徑為分層分析算法與實時分層分析算法計算得到的結果，實線路徑為Dijkastra算法計算得到的結果。表4是圖2對應的計算結果。圖3為黨校路出現(xiàn)堵塞時最優(yōu)路徑方案，其中虛線路徑(小間隔)為分層分析算法計算得到的結果，虛線路徑(大間隔)為實時分層分析算法計算得到的結果，實線路徑為Dijkastra算法計算得到的結果。橢圓是以軍民路與黨校路十字路口為新的起點和起火點為終點形成的橢圓搜索區(qū)。表5對應圖3計算結果。

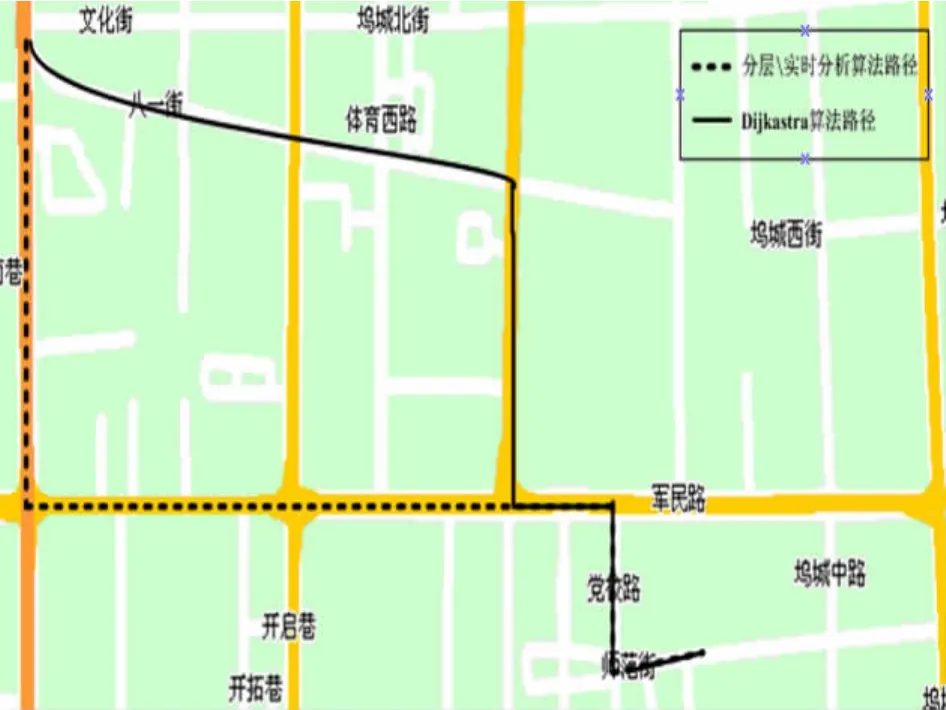
圖2 未出現(xiàn)局部堵塞時最優(yōu)路徑方案

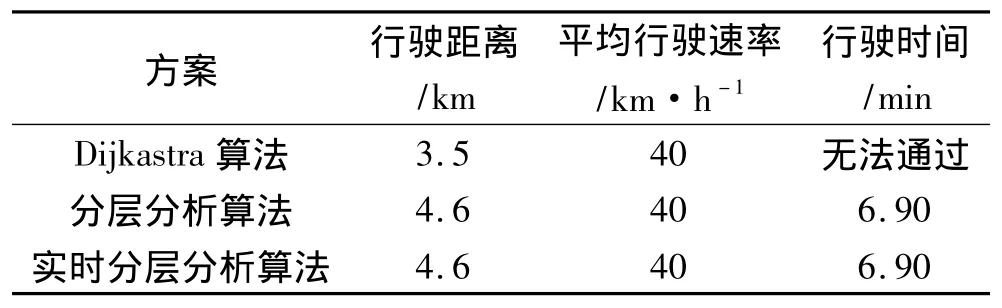
表4 在未出現(xiàn)局部堵塞時最優(yōu)路徑方案比較表

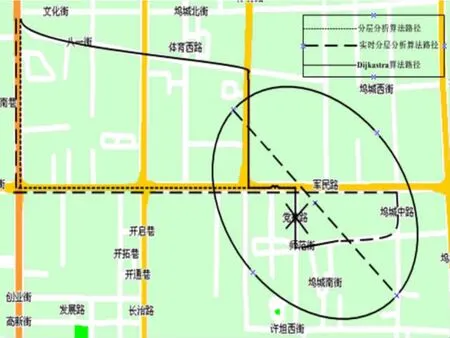
圖3 出現(xiàn)局部堵塞時最優(yōu)路徑方案

表5 出現(xiàn)局部堵塞時最優(yōu)路徑方案比較表

從視覺測量(圖2、3)及數(shù)理統(tǒng)計(表4、5)兩方面進行分析比較可知:(1)在未出現(xiàn)局部堵塞時，分層分析算法與實時分層分析算法得到最優(yōu)路徑方案相同，且都比Dijkastra算法得到的最優(yōu)路徑方案距離較長。但是Dijkastra算法得到的最優(yōu)路徑方案經過八一路是縣道，且路口較多，因而交叉路口延誤時間較長，會增加車輛行駛時間。同時，八一路較窄，僅能通過搶險救援消防車，而高空消防云梯車、水罐消防車無法順利通過，因而Dijkastra算法得到的最優(yōu)路徑方案不可行。而分層分析算法與實時分層算法得到最優(yōu)路徑方案經過平陽路與學府街是兩條省道，路口較少，可通過交通流量更大，同時路面寬敞，搶險救援消防車，高空消防云梯車及水罐消防車都可以順利通過，是該情況下的最優(yōu)路段選擇。(2)在出現(xiàn)局部堵塞時，以黨校路堵塞為例，Dijkastra算法得到路徑方案與未出現(xiàn)局部堵塞時相同，因而不具有可行性。實時分層分析算法得到的路徑方案在距離上較分層分析算法得到的路徑方案較長，但是分層分析算法路徑方案在堵塞路段等待通行時間未知，而實時分層分析算法得到的路徑方案是較分層分析算法得到的路徑方案的局部次優(yōu)方案，且到達起火點時間明確，因而實時分層分析算法得到的路徑方案是該情況下的最優(yōu)路段選擇。(3)將以上兩種情況生成的最優(yōu)路徑與實際情況進行比對，基本符合實際。

3 結論

本文在基于對分層分析算法最優(yōu)路徑的原理和特點的基礎上進行研究和分析，提出了一種實時的分層分析算法計算最優(yōu)路徑。該方法充分考慮路網(wǎng)狀態(tài)實時變化，使用局部規(guī)劃技術應對突發(fā)事件，修正全局路徑，保證車輛行駛時間最短。實驗結果及實際經驗均表明，與典型的Dijkastra算法及分層分析算法比較，該方法得到的最優(yōu)路徑方案均具有更強的可行性。

［1］AHUJA R K，MEHLHORN K，ORLIN J B，TARJAN R E.Faster algorithms for the shortest path problem［J］.Journal of the Association f or Computing Machinery，1990，37(2):213 －223.

［2］嚴寒冰，劉迎春.基于GIS的城市道路網(wǎng)最短路徑算法研討［J］.中國計算機學報，2002，(2):210 －215.

［3］魏新宇.消防滅火救援最優(yōu)路徑算法研究［D］.西安:西安科技大學，2006.

［4］唐文武，施曉東，朱大奎.GIS中使用改進的Dijkstra算法實現(xiàn)最短路徑的計算［J］.中國圖象圖形學報，2000，5(12):1019－1023.

［5］龍科軍，LEE D.HAN，王賽政.路網(wǎng)信息不完備條件下的動態(tài)最短路搜索［J］.計算機應用，2011，3(3):651 －653.

［6］王曉麗，楊兆升，呂旭濤，等.平行四邊形限制最短路徑算法及其在道路網(wǎng)絡中的應用［J］.吉林大學學報，2006，36(1):123～127.

［7］YAO Xin，LIU Yong，LIN Guang－ming.Evolutionary programming made faster［J］.IEEE Transactions on Evolutionary Computation，1999，3(2):82 －102.

［8］ZHONG Wei－cai，LIU Jing，XUE Ming－ zhi.A multi－ Agent genetic algorithm for global numerical optimization［J］.IEEE Transactions on Systems，Man，and Cybernetics Part B:Cybernetics，2004，34(2):1128－1141.

［9］LEUNG Y W，WANG Y P.An orthogonal genetic algorithm with quantization for global numerical optimization［J］.IEEE Transactions on Evolutionary Computation，2001，5(1):41 －53.

［10］SHANG Yun －wen，QIU Yu－h(huán)uang.A note on the extended rosenbrock function［J］.IEEE Transactions on Evolutionary Computation，2006，14(1):119 －126.