大跨度板架屈曲分析的非線性有限元法

劉相春，李陳峰，任慧龍，李曉宇

(1.海軍裝備部艦船辦，北京100071;2.哈爾濱工程大學船舶工程學院，黑龍江哈爾濱150001)

0 引言

屈曲破壞作為船舶結構的破壞形式之一，屈曲強度是船舶設計階段首要考慮的重要因素［1］。有限元法被廣泛地應用于復雜的屈曲分析:對于彈性屈曲問題，通常是求解特征值問題，求解臨界載荷;對于非線性屈曲問題，常用載荷增量法、位移控制的計算方法 (即弧長法)等。目前的屈曲分析方法在對大型船舶結構計算時，存在效率低，難以引入非線性，迭代計算收斂性差，無法計算復雜結構等問題。顯示動態分析的非線性有限元法是用慢速運動的ABAQUS/Explicit動態分析模擬靜態問題，采用中心差分法，對時間域上的動力特征進行積分，為處理復雜條件的非線性結構力學問題提供了強有力工具［2］。

極限強度定義的船體結構破壞形式計及了屈服、屈曲及組合的各種形式和各構件之間的非線性影響，結構達到承載能力極限狀態時，其破壞類型分為屈曲破壞和屈服破壞［3］。由此，進行極限強度分析以分析船體結構破壞形式，進而探討結構屈曲強度問題的方法，目前被認為是合理的。如何采用非線性有限元ABAQUS/Explicit方法，應用極限強度的分析思想，解決大跨度板架的屈曲問題顯得尤為重要。

1 板架結構的等效簡化

1.1 大跨度板架概述

某大型客滾船的大跨度雙層甲板板架，其結構型式非對稱、跨度大，參數如表1所示。

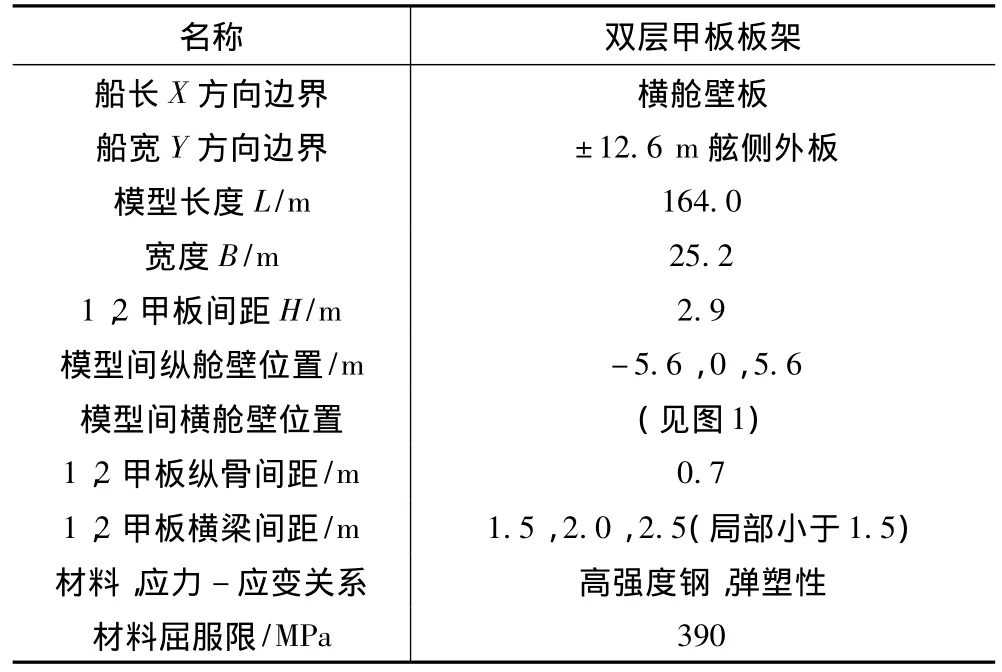
表1 某大型客滾船板架參數Tab.1 Grillage parameters of a Ro-Ro passenger ship

由于板架的有限元模型單元數目過多、自由度過大以及材料的非線性，對其應用弧長法、ABAQUS/Explicit方法等非線性有限元方法進行屈曲分析，受到計算機計算時間過長、收斂性問題的限制而很難完成。因此，對模型進行梁系等效簡化是必要的。一般在船舶設計初期進行板架穩定性的初步計算時，大都可以采用簡單板架的計算模型。該板架的長高比L/H為164.0/2.9，遠大于3倍，在構件型式及布置上均可視為空間梁系，因而采用空間梁系結構進行等效簡化是可行的。

1.2 板架結構梁系等效簡化

板架的縱艙壁和橫艙壁的編號及布置如圖1所示。縱艙壁L01～L03，橫向壁板T01～T13作為梁系的主體框架，1，2甲板及其他構件作為帶板計入其剖面參數計算，考慮剖面的垂向慣性矩I1，水平慣性矩I2，剖面面積A，剖面型心位置e(x，y，z)。

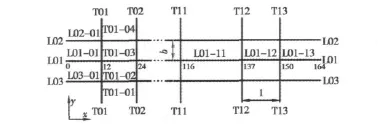
圖1 縱艙壁和橫艙壁編號及布置Fig.1 The number and disposal of longitudinal and transverse bulkheads

根據文獻 ［4］中關于“結構穩定性校核”的規定，確定受壓構件的帶板寬度。單跨帶板構件的歐拉應力計算公式為

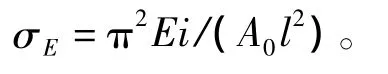
式中:σE為單跨帶板縱骨理論歐拉應力;i為單跨帶板受壓構件剖面面積;A0為單跨帶板受壓構件剖面面積;l為縱桁(縱艙壁)間距;b為強橫梁 (橫向壁板)間距;φ=σE/σS，σS為材料屈服限。

由此計算各艙壁板連帶板的剖面參數，完成后對各剖面數據進行等效［5］:根據慣性矩I，面積A，型心位置e等效的原則，編寫梁截面等效Fortran程序:根據剖面形式特點，選用I型截面梁，程序輸入為慣性矩I1，I2，截面面積A，輸出為I型截面梁的各參數。根據梁系等效簡化結果建立有限元模型，如圖2所示。

圖2 等效簡化梁系有限元模型Fig.2 FE model of the simplified equivalent beams

1.3 邊界條件與載荷施加

對于受到周圍構件支持的船舶板架結構，四邊對轉角的約束程度既不是極小值也不是極大值，而是具有一定大小的彈性轉角約束。但在目前基于非線性強度分析與設計方法中，為了簡化及偏于安全起見，一般都取為四邊簡支約束。出于同樣的考慮，對等效梁系模型進行四邊簡支約束。

根據實船板架受力特點，對梁系施加軸向壓力載荷:特征值屈曲分析時，DC邊 (見圖3)沿x軸負向施加集中載荷Fx;非線性有限元分析時，DC邊沿x軸負向施加位移載荷ux，分析時間內線性加載。

圖3 梁系的邊界條件與載荷Fig.3 Boundary conditions and loads of beams

2 特征值屈曲分析

2.1 目的

特征值屈曲分析又稱線彈性失穩 (第一類穩定)分析，分析的目的旨在:不考慮結構非線性因素的影響，尋找結構在屈服限σS范圍之內的失穩臨界點 (極限載荷的上限)，即屈曲歐拉應力σE，研究結構在特定載荷下的穩定性、結構失穩載荷以及與非線性有限元屈曲分析結論的一致性驗證。

結構取線彈性材料，不考慮結構的型心偏置，采用MSC.Nastran軟件進行特征值求解得到的臨界應力值，在許多情況下與實際工程中一般表現的第二類失穩破壞的臨界值相差不大，因此特征值屈曲分析仍有重要的工程意義。

2.2 分析

MSC.Nastran軟件對線性屈曲問題的分析，是通過提取使線性系統剛度矩陣奇異的特征值來獲取結構的臨界失穩載荷及失穩模態。因此，臨界屈曲載荷Fcr=屈曲特征值BEi×靜態載荷FS，從而σcr=Fcr/A，A為結構斷面面積。找出結構的前二階失穩模態，結果如表2所示。

表2 歐拉應力σE計算表Tab.2 Calculation table of Euler stress σE

歐拉應力σE為836.3 MPa，根據船舶設計穩定性要求:在占一半船長的中部區域，整體板架的縱向骨架的歐拉應力與其材料屈服極限的比值不小于1.5～2.0，該大跨度板架σE/σS≈2.144，滿足上述要求。

此外，基于線彈性分析方法，在屈服限范圍內無法找到結構的屈曲歐拉應力σE。在壓潰破壞的情況下，材料非線性是更為重要的非線性因素，需對其進行非線性屈曲分析，得出結構破壞的極限狀態應力。

3 非線性分析ABAQUS/Explicit方法

3.1 顯式動態分析的有限元法

非線性有限元分析方法很好地考慮了影響船體結構極限承載能力、破壞形式的一些敏感因素，例如材料的彈塑性屬性、結構的幾何非線性行為以及結構的屈曲強度和后屈曲強度等。

ABAQUS/Explicit顯式動態分析 (準靜態)的優勢在于解決非線性問題。它采用中心差分法顯式對運動方程在時間域上進行積分，利用上一個增量步的平衡方程動態地計算下一增量步的狀態，其顯式動力學求解過程如下:

1)節點計算

節點計算包括求解動力平衡方程，對時間顯式積分確定加速度、速度和位移。

動力平衡方程為

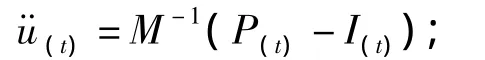
對時間顯式積分為

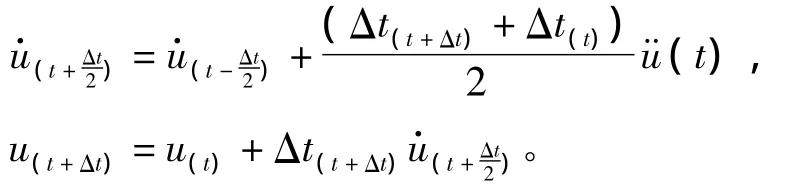
2)單元計算

單元計算包括確定單元應變和應用材料本構關系 (單元剛度)，確定單元應力，然后計算內力。

①根據應變速率ε·，計算單元應變增量dε。

②根據本構關系計算應力σ，

③ 匯集節點內力I(t+Δt)。

3)設置t+Δt為t，返回步驟1)。

ABAQUS/Explicit的求解僅依賴于一個穩定增量步長，而與載荷的類型和持續時間無關。隨著載荷的施加，結構剛度劇烈變化，由于在分析過程中不需要形成總體剛度矩陣，也不必為求解總體平衡方程進行迭代計算，因此ABAQUS/Explicit非線性有限元分析可以高效地求解復雜的非線性問題。

3.2 大跨度板架屈曲分析

基于極限強度的分析思想，由應力-應變關系曲線 (見圖4)判斷結構的破壞形式。根據曲線1和曲線2可以認為板架的整體穩定性較好，發生的主要破壞形式是屈服破壞［6］;曲線3則表明由于發生屈曲結構整體崩潰，即屈曲破壞。

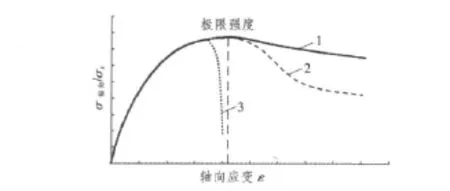
圖4 彈塑性材料軸向作用應力-應變關系曲線Fig.4 Stress-strain relation curve of plastic material

該大跨度板架的有限元分析參數設置與分析結果如表3～表5，圖5～圖8所示。

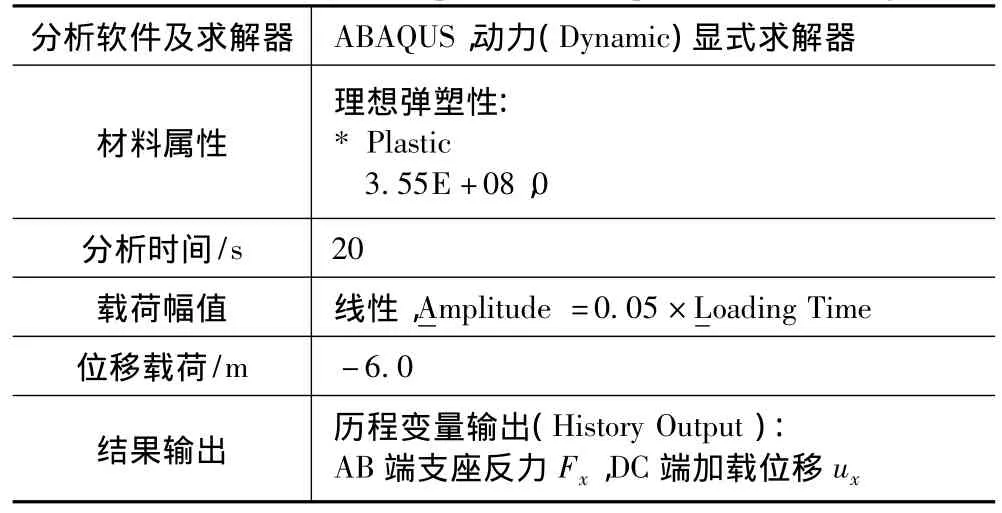
表3 非線性有限元分析參數設置Tab.3 ABAQUS/Explicit NFEM parameters setting

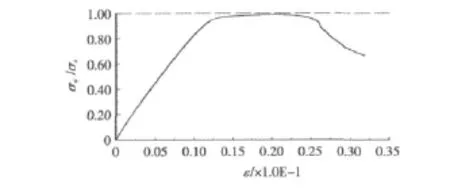
圖5 梁系結構應力-應變曲線Fig.5 Stress-strain relation curve of beam component

圖5為結構達到極限狀態的應力-應變曲線。圖中橫坐標表示結構的應變ε，縱坐標表示結構的應力σx與材料屈服應力的比值σs，即為無量綱系數 σx/σs，其中，σx=Fx/A。

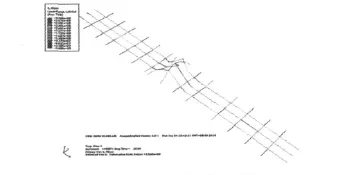
圖6 梁系極限狀態 (變形放大系數=2.5)Fig.6 Ultimate state of beam(magnify coefficient of distortion=2.5)

表4 極限狀態臨界應力σcr計算表Tab.4 Calculation table of ultimate state critical stress

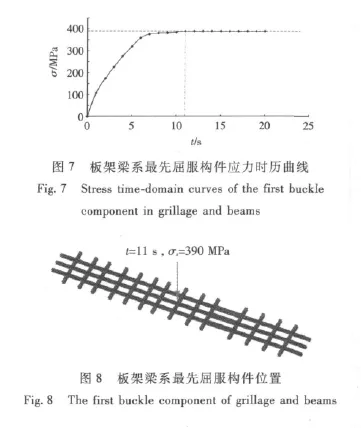
由圖5、圖6及表4所示，σcr/σS≈0.957接近于規范對其0.97的要求。梁系結構在加載至15.811 6 s，應變量為0.025 03時，結構承載能力下降，在結構達到屈曲臨界應力前，由圖7和圖8可知，結構在加載至11 s時，構件首先出現屈服，直至結構破壞。

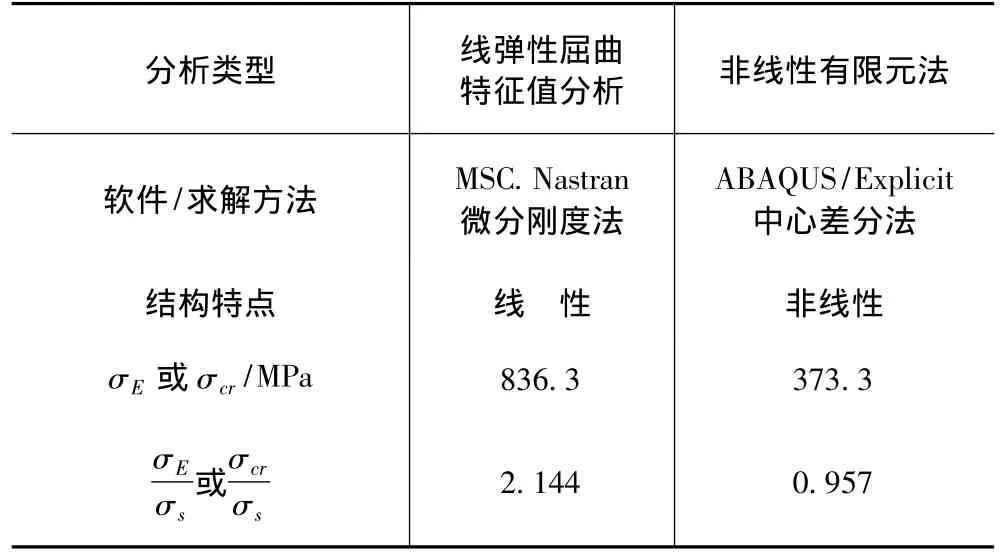
表5 歐拉應力σE與臨界應力σcr計算結果比對Tab.5 Calculation results contrast table of Euler stress σEand critical stress σcr

由表5分析結果可知，線性屈曲特征值分析與非線性有限元分析均得到了σE或σcr，并滿足規范對其與屈服限比值的要求。

4 結語

采用結構等效的方式，對大跨度板架進行空間梁系簡化，給大跨度板架屈曲分析提供了新思路，有效地解決了大跨度板架屈曲穩定性分析困難的問題。

特征值屈曲分析得到的大跨度板架的歐拉應力大于材料屈服限，即基于線彈性分析方法，在屈服限范圍內無法找到結構的屈曲歐拉應力，該板架在結構屈服破壞前不會發生整體屈曲破壞。

通過ABAQUS/Explicit非線性有限元分析，得到該大跨度板架的極限強度接近材料的屈服應力，可以認為該板架的整體穩定性較好，這與特征值屈曲分析得出的分析結論是一致的。因此，本文方法對大跨度板架的屈曲分析具有優越性和重要意義。

［1］束長庚，周國華.船舶結構的屈曲強度［M］.北京:國防工業出版社，2003.SHU Chang-gen，ZHOU Guo-hua.Buckle strength of ship structure［M］.Beijing:National Defence Industry Press，2003.

［2］ABAQUS/Explicit有限元軟件入門指南［M］.莊茁，等譯.北京:清華大學出版社，1999.33-37.

［3］彭可可，賀國京.大跨度橋梁極限承載力的雙重非線性分析［J］.中南林學院學報，2006，26(3):74-76.PENG Ke-ke，HE Guo-jing.Dual nonlinear analysis of the ultimate load apacity of long-span bridge［J］.Journal of Central South Forestry University，2006，26(3):74-76.

［4］中國船級社.鋼質海船入級與建造規范［S］.2006，2(1):333-340.China Classification Society.Rules and regulations for the construction and classification of sea-going steel ships［S］.2006，2(1):333-340.

［5］萬琪，王福花.大跨度無支撐甲板縱向穩定性分析和優化設計［J］.中國造船，2011(1):17-25.WAN Qi，WANG Fu-hua.Longitudinal stability analysis and optimum design of supportless long-span deck structure［J］.Shipping of China，2011(1):17-25.

［6］周海仲.船體結構極限強度的非線性有限元分析［D］.哈爾濱工程大學，2010.70-71.ZHOU Hai-zhong.The ultimate strength analysis of the ship structures based on NFEM［D］.Harbin Engineering University，2010.70-71.