多起伏濕氣集輸管線工藝計算方法優選

李玉浩 曹學文 梁法春 張 俊 趙文祥

1．中國石油大學（華東）儲運與建筑工程學院 2．中國石化中原油田普光分公司

在山地丘陵地區的高含硫氣田開發過程中，考慮到工藝安全、經濟效益以及環境保護等因素，濕氣集輸工藝得到廣泛應用［1－4］。因此，多起伏低持液率天然氣集輸管線的工藝計算就成為當前亟待解決的問題之一。縱觀當前國內外的研究成果，諸多學者以實驗為基礎提出了多種氣液兩相流管路工藝計算方法，但這些計算方法大都是在短距離、低壓力、小管徑的實驗條件下得出的，其適用范圍具有一定的局限性，需要加以分析研究，選擇合適的計算方法準確預測多起伏濕氣集輸管線的積液和壓降，為高含硫濕氣集輸管線的高效運行和清管方案制訂等提供依據［5－10］。鑒于此，筆者以常用多相流管路工藝計算模型程序為基礎，將預測結果與現場生產數據進行對比，評估了Beggs ＆Brill相關式、Mukherjee ＆Brill相關式、Xiao ＆Brill模型、Eaton－Flanigan相關式、DuklerⅡ－Flanigan相關式的積液判斷和壓降預測效果，篩選出了適用于多起伏濕氣集輸管線現場、精度較好的計算方法。

1 常見工藝計算方法

目前常用的氣液兩相流管路工藝計算方法主要有以下幾種［11］：①Beggs ＆ Brill相關式；②Mukherjee＆Brill相關式；③Xiao＆Brill模型；④Eaton－Flanigan相關式；⑤DuklerⅡ－Flanigan相關式。

Beggs ＆Brill相關式是在動量方程的基礎上進行理論推導得出的與管路傾角有關的兩相流壓降關系式［12］。其中截面含液率和兩相水力摩阻系數是通過分析在小型試驗系統上測得的584組實驗數據而確定的，該小型試驗系統由長27．43m、內徑分別為25．4 mm和38．1mm的有機玻璃管組成，實驗介質為水和空氣。

Mukherjee ＆Brill相關式提出了一組以無因次準數表示并且適用于各種管路傾角的流型轉換方程［13］。管路壓降由重力壓降、加速壓降、摩阻壓降3部分組成，各部分壓降計算式根據不同流型的流動機理給出。截面含液率是在實驗數據的基礎上應用非線性方程回歸確定的。實驗數據是在管徑為38．1mm、長9．75m、傾角范圍為－90°～＋90°的管路系統上測得的，實驗介質為煤油和空氣。

Xiao ＆Brill模型是關于水平及近水平管中氣液兩相流動的綜合機理模型［14］，其中兩相流動流型被分為4種：分層流（包括分層光滑流和分層波浪流）、間歇流（包括氣團流和段塞流）、環狀流和分散氣泡流。此模型提出了流型的判別準則，并通過理論推導，應用必要的經驗關系式給出了每種流型下截面含液率和管路壓降的計算方法，經大量現場生產數據和實驗室數據評估，模型預測效果較好。

Eaton－Flanigan相關式為混合模型工藝計算方法［15］。其中兩相流管線的持液率采用Eaton持液率相關式計算得出，在能量平衡方程式基礎上推導出的Eaton壓降相關式可以計算管路的摩阻壓降和加速壓降，高程造成的壓降損失由Flanigan相關式決定。

DuklerⅡ－Flanigan相關式為另一種常用的混合模型工藝計算方法［16］。兩相流管線截面含液率通過DuklerⅡ相關式中截面含液率—體積含液率－兩相雷諾數的關系曲線得出。DuklerⅡ相關式和Flanigan相關式分別給出了兩相管路摩阻壓降和重力壓降的計算方法，模型忽略了加速壓降的影響。

筆者考慮壓降、溫降的變化所導致的熱物性參數的變化，選擇BWRS狀態方程進行多組分相平衡計算，采用C語言編制了以上5種常見工藝計算相關式及模型的計算程序。程序中Eaton和DuklerⅡ相關式計算的傾斜管持液率用Beggs ＆Brill相關式進行了修正。

2 工藝計算方法的選取

2．1 多起伏濕氣集輸管線概況

中國石化普光氣田屬于典型的高含硫氣田，地面集輸系統采用了濕氣集輸工藝，且氣田地處地形條件復雜的高山丘陵地區，管線起伏變化頻繁，管內積液嚴重。圖1為普光氣田P201站至集氣末站的管線縱斷面圖，管線總長5 561．4m，由113個起伏點和112段起伏管路組成，平均管段長度僅為49．66m，而且管段平均起伏角度偏大，其中22．4%的管段傾角絕對值大于20°，管段傾角絕對值大于10°的管段更是超過了50%。管線輸送的濕天然氣平均分子量為21．15，其中C3＋組分的摩爾分數為零，水是管線內液相的主要成分，其摩爾分數為2．28%。因此，此管線屬于典型的多起伏低持液率集輸管線。管線其他數據如下：內徑為463．6mm；相對粗糙度為0．000 215 7；總傳熱系數為6．24W／（m2·℃）。

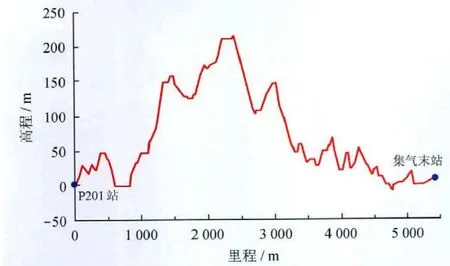
圖1 普光氣田P201站至集氣末站的管線縱斷面圖

2．2 持液率計算方法的選取

持液率計算是壓降計算的基礎，在多相流管線的工藝計算中處于重要地位。持液率不但會影響集氣末站氣液分離器外形和尺寸的設計，而且對于清管周期及清管方案的制訂具有決定性作用［17］。因此，篩選并確定適用于多起伏低持液率集輸管線的持液率計算方法對于山地丘陵地區濕氣集輸管線的初步設計和保證管線的高效運行具有重要意義。

多起伏管線是由水平管段、向上傾斜管段、向下傾斜管段組成的復雜管道，受地形起伏影響，不同傾角管段中的氣液兩相流動流型可能有所不同，而每種流型有其特有的氣液分布特征，因此，需要分別為水平管段、向上傾斜管段、向下傾斜管段選取持液率計算方法。在低持液率向下傾斜管段內，氣液主要流動型態為分層流，此條件下采用Xiao ＆Brill模型預測管內持液率準確度較好［18－19］。對于水平管段，為了比較各相關式的計算精度，應用超聲積液檢測裝置對P201站至集氣末站管線的某水平管段進行了液位監測，獲得了氣液流動達到基本穩定時的平均持液率，并與各相關式預測值進行了對比（圖2）。

從圖2可以看出，由Beggs ＆Brill相關式和Xiao＆Brill模型得到的水平管持液率偏大，而DuklerⅡ相關式的預測值偏小，同現場檢測結果相比，這3種相關式的計算值誤差都很大，這是因為濕天然氣含液量少，管線持液率低，比較小的計算偏差就會引起較大誤差。通過 Mukherjee ＆Brill相關式計算得到的持液率誤差較小，能夠滿足工程應用要求，但是精度不如Eaton相關式，Eaton相關式的計算結果與現場檢測結果十分接近，準確性好，適合用于多起伏低持液率管線水平管段的持液率預測。

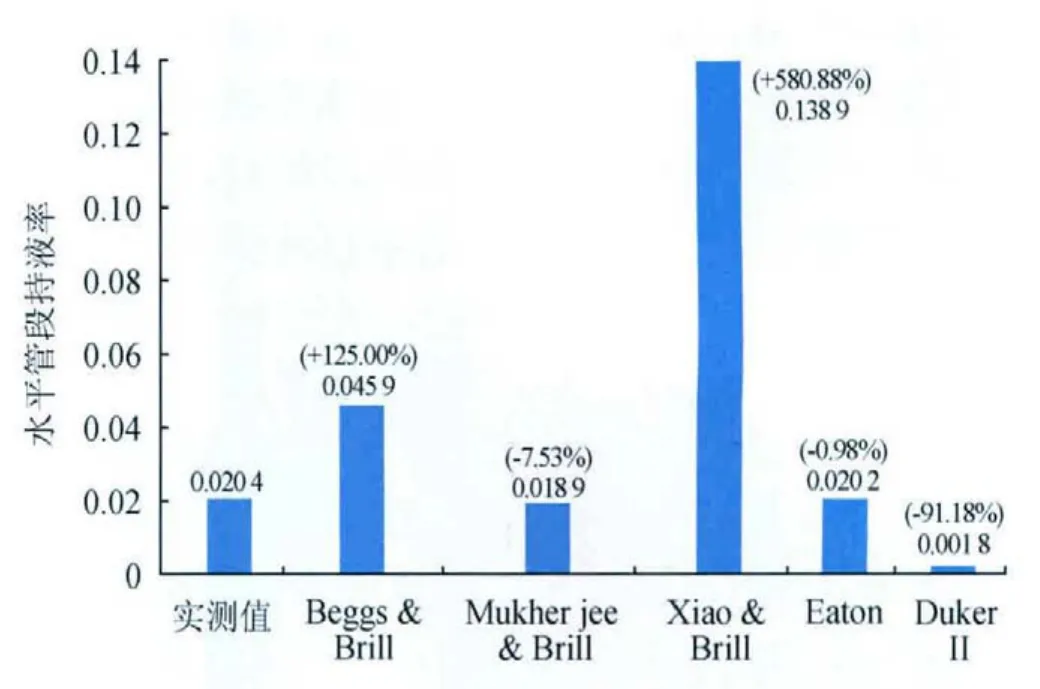
圖2 水平管段持液率預測結果與實測值的對比圖

由于向上傾斜管段中流動比較復雜，因此，本文采用，5種常見工藝計算方法分別對其進行持液率計算，結合向下傾斜管段和水平管段的持液率預測結果，得到P201站至集氣末站管線的積液量，與現場生產數據進行對比分析，結果如表1所示。

由表1可以看出，當向上傾斜管段使用Xiao ＆Brill模型計算時得到的管線積液量偏大，采用Mukherjee ＆Brill、Eaton以及DuklerⅡ相關式得出的預測結果偏小，而且這些相關式的預測值誤差都很大。當向上傾斜管段采用Beggs ＆Brill相關式、水平管段采用Eaton相關式、向下傾斜管段采用Xiao ＆Brill相關式計算得到的管線積液量誤差較小，能夠為多起伏低持液率集輸系統的設計和運行提供比較準確的結論。

2．3 壓降計算方法的選取

壓降計算是多起伏低持液率集輸管線工藝計算的最終目的。壓降預測是管線進口壓力設計和中間泵站布置的基礎。但是，在多起伏低持液率管線的設計和運行模擬中選擇正確合理的壓降計算方法存在一定的難度，本文通過對比分析現場運行數據和常用工藝計算方法的計算結果，篩選出適用于多起伏低持液率管線、精度較高的壓降計算方法。

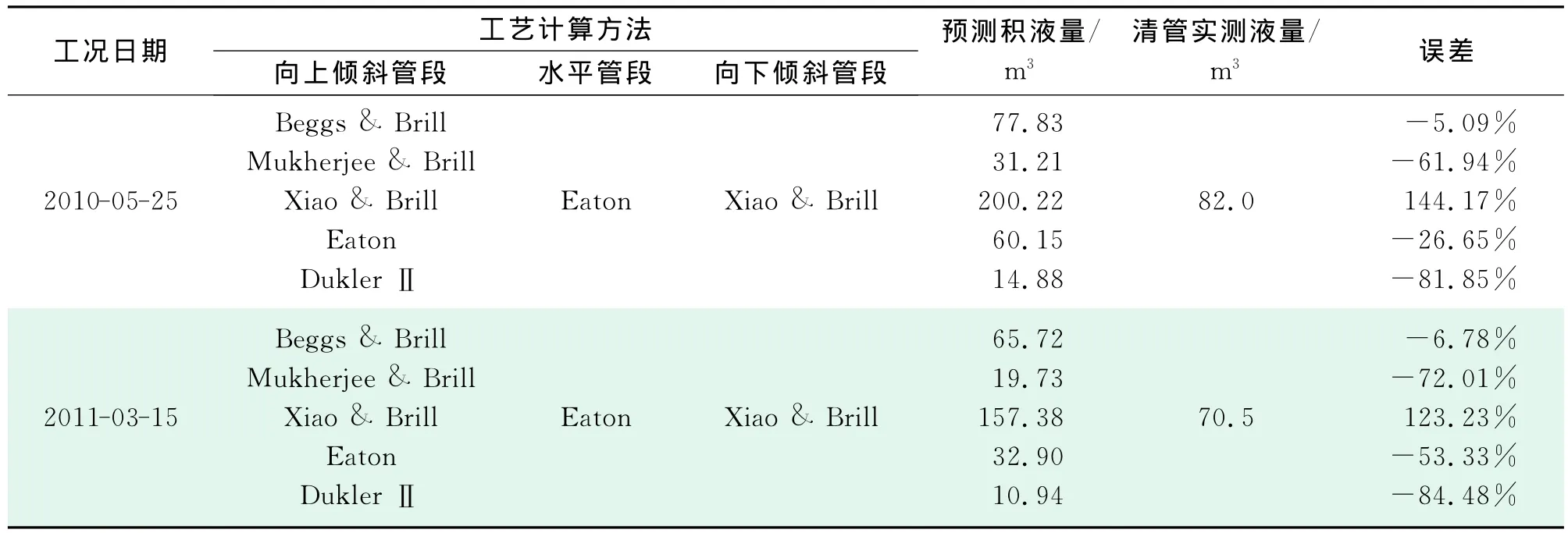
表1 不同工況下的積液量預測表

以普光氣田P201站至集氣末站的集輸管線2011年3月12日的運行工況為例，在管線出口壓力一定的條件下，用多種工藝計算方法分別計算管線進口及沿線9個閥室的壓力，預測出管線的壓力變化趨勢，與現場運行數據進行對比（圖3）。

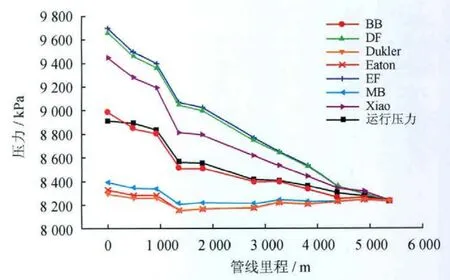
圖3 多起伏低持液率管線壓降預測結果與運行數據的對比圖

從圖3可以看出，Eaton相關式和DuklerⅡ相關式預測的管段壓力變化趨勢相近，在1 000m后兩者的壓力曲線更是幾乎重合，但是由于忽略了高程壓降，導致壓降值過小。考慮了多起伏管線高程變化引起壓降損失的 Eaton－Flanigan相關式和 DuklerⅡ－Flanigan相關式計算得到的壓降值過大，顯然，其中的Flanigan相關式過高地估計了低持液率管線中的高程壓降損失。Mukherjee ＆Brill相關式和Xiao ＆Brill模型的壓降預測值分別偏小和偏大，使用時會產生較大誤差。與實際運行壓力相比，由Beggs ＆Brill相關式得到的進出口壓降值略大，沿線壓力變化趨勢相近，因此，Beggs ＆Brill相關式計算多起伏低持液率管線的壓力變化準確度較高。

應用Beggs＆Brill相關式預測多種運行工況下的管線壓降值，與生產數據進行對比（圖4）。由圖4可知，預測的壓降值與實際壓降值誤差較小，進一步驗證了Beggs ＆Brill相關式能夠比較準確地預測多起伏低持液率管線的壓降值，對于此類管線的設計及運行模擬有較好的指導作用。

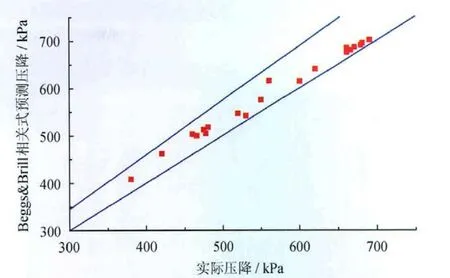
圖4 Beggs ＆Brill相關式壓降值預測結果與運行數據對比圖

3 結論

1）與其他常用工藝計算方法相比，Eaton相關式能夠比較準確地預測多起伏低持液率管線水平管段的持液率。

2）向上傾斜管段采用Beggs ＆Brill相關式、水平管段采用Eaton相關式、向下傾斜管段采用Xiao ＆Brill相關式計算多起伏低持液率管線的積液量時誤差較小。

3）就多起伏低持液率管線而言，Eaton相關式、DuklerⅡ相關式以及Mukherjee ＆Brill相關式預測的壓降值偏小，而由Eaton－Flanigan相關式、DuklerⅡ－Flanigan相關式及Xiao ＆Brill相關式計算得到的壓降值偏大。Flanigan相關式過高地估計了低持液率管線中的高程壓降損失。

4）對比分析及多種運行工況驗證表明，由Beggs＆Brill相關式計算得到的壓降值與現場管線的實際壓降值吻合較好，可以用于多起伏低持液率管線的壓降值預測。

［1］馮叔初，郭揆常．油氣集輸［M］．東營：中國石油大學出版社，2006：91．FENG Shuchu，GUO Kuichang．Oil ＆ Gas Gathering and Transportation［M］．Dongying：China University of Petroleum Press，2006：91．

［2］宋華軍，戴永壽，楊濤，等．天然氣管道積液紅外成像檢測方法［J］．天然氣工業，2012，32（5）：62－65．SONG Huajun，DAI Yongshou，YANG Tao，et al．The infrared imaging method for measuring the liquid contents in natural gas pipelines［J］．Natural Gas Industry，2012，32（5）：62－65．

［3］李自力，孫云峰，張子波，等．普光高含硫氣田集輸管網優化［J］．石油學報，2011，32（5）：872－876．LI Zili，SUN Yunfeng，ZHANG Zibo，et al．Optimization design of a gathering pipe network of natural gas with high H2S from the Puguang Gas Field［J］．Acta Petrolei Sinica，2011，32（5）：872－876．

［4］張青勇．從川氣東送管道工程投產探討天然氣長輸管道投產工藝［J］．石油與天然氣化工，2011，40（1）：90－94．ZHANG Qingyong．Discuss of long－distance natural gas pipeline commissioning processes from Sichuan to Eastern China gas transmission pipeline project［J］．Chemical Engineering of Oil ＆ Gas，2011，40（1）：90－94．

［5］YUAN Hong，ZHOU Desheng．Simulating a hilly terrain pipeline using two－phase flow correlations and mechanistic models［C］∥SPE Production and Operations Symposium，4－8April 2009，Oklahoma City，Oklahoma，USA．New－York：SPE，2009．

［6］喻西崇，馮叔初．起伏多相管流壓降計算方法的研究［J］．油氣田地面工程，2000，19（5）：1－2．YU Xichong，FENG Shuchu．Calculation methods of pressure drop in undulated multiphase pipelines［J］．Oil－Gas Field Surface Engineering，2000，19（5）：1－2．

［7］喻西崇，趙金州，馮叔初．起伏多相流管路持液率計算方法研究［J］．西南石油學院學報，2000，22（3）：94－97．YU Xichong，ZHAO Jinzhou，FENG Shuchu，et al．The prediction method of holdup in undulated multiphase pipelines［J］．Journal of Southwest Petroleum Institute，2000，22（3）：94－97．

［8］曹學文，梁法春，黃慶宣，等．水平管氣液分層流壓力梯度和含氣率計算方法研究［J］．西安交通大學學報，2003，7（5）：444－446．CAO Xuewen，LIANG Fachun，HUANG Qingxuan，et al．Study on the calculation of pressure gradient and void fraction in horizontal gas－liquid two－phase stratified flow［J］．Journal of Xi’an Jiaotong University，2003，7（5）：444－446．

［9］薛成剛，趙繼寬，詹衛國．水平與微傾斜兩相段塞流中持液率計算新方法［J］．國外油氣田工程，2011，17（2）：13－15．XUE Chenggang，ZHAO Jikuan，ZHAN Weiguo，et al．A new model for liquid holdup calculation of gas－liquid slug flow in horizontal and near－horizontal tubes［J］．Foreign Oilfield Engineering，2011，17（2）：13－15．

［10］董正遠．地形高程差對天然氣輸送管道工藝計算的影響［J］．西安石油大學學報，2007，22（5）：41－43．DONG Zhengyuan．Effect of topographic difference on the technological calculation of natural gas transportation pipeline［J］．Journal of Xi’an Shiyou University，2007，22（5）：41－43．

［11］BASNIEV K S，DMITRIEV N M，CHILINGAR G V．Two－phase flow in pipes［M］．Tulsa：Tulsa University Fluid Projects，1991．

［12］BEGGS D H，BRILL J P．A study of two－phase flow in inclined pipes［J］．Journal of Petroleum Technology，1973，25（5）：607－617．

［13］MUKHERJEE H，BRILL J P．Inclined two－phase flow correlations design manual［M］．Tulsa：Tulsa University Fluid Projects，1981．

［14］XIAO J J，SHAOHAM O，BRILL J P．A comprehensive mechanistic model for two－phase flow in pipelines［C］∥SPE Annual Technical Conference and Exhibition，23－26 September 1990，New Orleans，Louisiana，USA．New－York：SPE，1990．

［15］EATON B A，KNOWLES C R，SILBERBRG I H．The prediction of flow pattern，liquid holdup and pressure losses occurring during continuous two－phase in horizontal pipelines［J］．Journal of Petroleum Technology，1967，19（6）：815－828．

［16］DUKLER A E．Gas－liquid flow in pipelines［M］．Washington DC：American Gas Association，1969．

［17］梁法春，曹學文，魏江東，等．積液量預測方法在海底天然氣管道中的應用［J］．天然氣工業，2009，29（1）：103－105．LIANG Fachun，CAO Xuewen，WEI Jiangdong，et al．Application of accumulated liquid volume prediction method in submarine gas pipeline［J］．Natural Gas Industry，2009，29（1）：103－105．

［18］TAITEL Y，DUKLER A E．A model for predicting flow regine transitions in horizontal and near horizontal gas－liquid flow［J］．American Institute of Chemical Engineers Journal，1976，22（1）：37－45．

［19］YUAN Hong，ZHOU Desheng．Evaluation of two－phase flow correlations and mechanistic models for pipelines at inclined downward flow［J］∥SPE Eastern Regional／AAPG Eastern Section Joint Meeting，11－15October 2008，Pittsburgh，Pennsylvania，USA．NewYork：SPE，2008．