有限生成模自同態環的一種刻畫*

王飛飛， 鄭清月， 趙燕波， 陳淼森

(浙江師范大學 數理與信息工程學院,浙江 金華 321004)

有限生成模自同態環的一種刻畫*

王飛飛， 鄭清月， 趙燕波， 陳淼森

(浙江師范大學 數理與信息工程學院,浙江 金華 321004)

定義了矩陣環的零化子，對有限生成模的自同態環進行了刻畫．證明了有限生成左R-模的自同態環是環R上矩陣環的一個子環的同態像，并利用此結果給出了代數學中一些經典結論的新的證明．

零化子；有限生成模；自同態環；矩陣環

0 引 言

模的自同態是代數學的一個重要研究對象．刻畫模的自同態環可以推廣線性代數的一些經典結論[1]，也可以為模的研究提供一種途徑[2-3]．因此，研究模的自同態具有很好的理論意義．Goldie等[4]通過構造Goldie環刻畫了Noether環上有限生成模的自同態環，從而推廣了Levitski定理．本文通過定義矩陣環的零化子，刻畫了一般環上有限生成模自同態環的結構，從而用新的方法證明了代數學中一些經典的結論．

本文中的環R均指具有單位元的結合環,模RM指幺作用左R-模．采用文獻[5]中的規定，記End(RM)=EndrR(M)，即對于左R-模，將自同態作用在元素的右邊．

1 循環模的自同態環

定義1[5]對于模RM的非空子集X，稱l(X)={r∈R|rX=0}為X在R中的(左)零化子，簡稱X的零化子．特別地，當X={a}時，記l(a)=l(X)；當X=M時，記AnnR(M)=l(M)．

易知，對于模RM的任意非空子集X，l(X)是R的左理想．若X又是RM的子模，則l(X)是R的理想．

引理1對于模RM，任意m∈M，環R的子集I={r∈R|l(m)r?l(m)}是R的子環，且l(m)是I的理想．

證明 顯然，環R的單位元1∈I．對于任意r1,r2∈I，有

l(m)(r1+r2)?l(m)r1+l(m)r2?l(m)+l(m)=l(m)，

從而r1+r2∈I．又因為l(m)(r1r2)=(l(m)r1)r2?l(m)r2?l(m)，所以r1r2∈I．因此，I是R的子環．l(m)是R的左理想，自然也是I的左理想．又由I的定義可知，l(m)也是I的右理想．所以，l(m)是R的理想．證畢．

定理1循環模RM的自同態環同構于R的子環的商環．

證明 設RM的生成元為m，則M=Rm．由引理1知，I={r∈R|l(m)r?l(m)}是R的子環，l(m)是I的理想．接下來分3步證明End(RM)?I/l(m)．

1)構造映射φ．先構造從End(RM)到I/l(m)的對應法則φ．對任意f∈End(RM)，若(m)f=rm，則取f在φ作用下的像為r在I/l(m)中的等價類，即φ(f)=r+l(m)．因為f是模RM的自同態，所以(0)f=0，即對任意r0∈l(m)，有(r0m)f=r0(m)f=r0rm=0成立，即l(m)r?l(m)成立，因此r∈I．假設f′∈End(RM)，(m)f′ =r′m．若f=f′，則

rm=r′m?(r-r′)m=0?r-r′∈l(m)?r+l(m)=r′+l(m)，

即φ(f)=φ(f′)．所以，φ是End(RM)到I/l(m)的一個映射．

2)證明φ是環同態．對于任意f1,f2∈End(RM)，設(m)f1=r1m，(m)f2=r2m，于是

(m)(f1+f2)=(m)f1+(m)f2=r1m+r2m=(r1+r2)m，

即φ(f1+f2)=r1+r2=φ(f1)+φ(f2),(m)(f1f2)=(m)f1f2=(r1m)f2=r1(m)f2=r1r2m,也就是φ(f1f2)=r1r2=φ(f1)φ(f2).

3)證明φ是同構．假設φ(f1)=φ(f2),φ(f1)=r1+l(m),φ(f2)=r2+l(m)，于是r1-r2∈l(m)?r1m=r2m?f1=f2．所以，φ是單射．又對于任意r"+l(m)∈I/l(m)，可以證明f(rm)=rr"m是模M的自同態．假設r1m=r2m，則有(r1-r2)m=0?r1-r2∈l(m)．于是對r"∈I，有(r1-r2)r"∈l(m)，即(r1-r2)r"m=0?r1r"m=r2r"m．所以f是RM到自身的一個映射．易證f是模同態.因此，φ是滿射．證畢．

當R是交換環時，定理1中I=R，即可得以下推論:

推論1假設R是交換環，則循環R-模M的自同態環同構于R的商環．

又當R是交換環，且循環R-模M是忠實時，定理1中l(m)?AnnR(M)=0，從而可得以下推論:

推論2假設R是交換環，則忠實循環R-模的自同態環同構于R．

利用定理1可以對以下熟知的結論給出新的證明．

定理2[6]正則模RR的自同態環同構于R．

證明 由于正則模RR為循環模，且生成元為1，所以l(1)=0，I={r∈R|l(1)r?l(1)}=R．由定理1即得End(RR)?R．證畢．

定理2也說明存在非交換環上的忠實循環模RM，它的自同態環同構于R．

利用定理1亦可證明著名的Schur引理．

定理3(Schur引理) 若RM是單模，則End(RM)為除環．

證明 設RM是單模，于是對于任意0≠m∈M，有M=Rm．由定理1知，End(RM)?I/l(m)．對于任意I/l(m)中的非零元r+l(m)，因為r?l(m)，所以rm≠0．由RM是單模知R(rm)=M．因此，存在x∈R，使得xrm=m，即(xr-1)m=0?xr-1∈l(m)，也即存在x+l(m)∈I/l(m)，使得

(x+l(m))(r+l(m))=1+l(m)．

從而證明了I/l(m)中任意非零元均有左逆元，則I/l(m)是除環，即End(RM)為除環．證畢．

2 有限生成模的自同態環

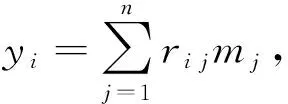
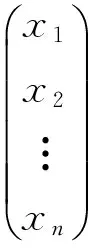
定義2對于模RM中的n個元m1,m2,…,mn，記ξ=(m1,m2,…,mn)′，稱矩陣環MatnR的子集

為n元組(m1,m2,…,mn)在MatnR中的(左)零化子，簡稱(m1,m2,…,mn)的零化子．

命題1對于模RM的任意n個元m1,m2,…,mn，l(ξ)是矩陣環MatnR的左理想．

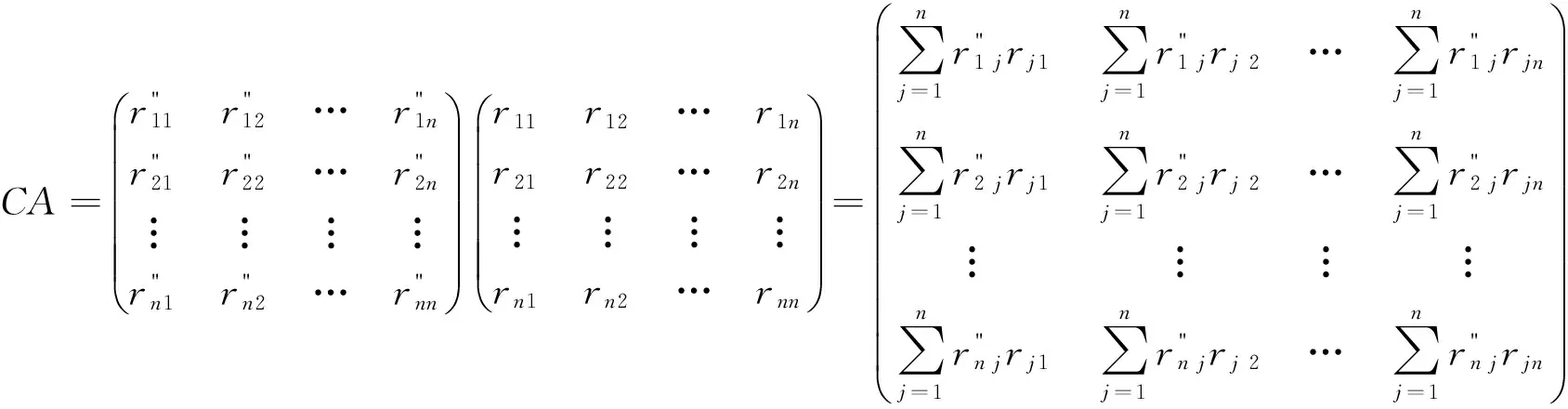
對于任意1≤i≤n，

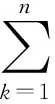
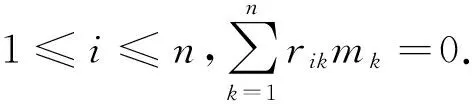
即CA∈l(ξ)．于是，l(ξ)是MatnR的左理想．證畢．

不難證明以下引理:

引理2對于模RM的任意個n元m1,m2,…,mn，矩陣環MatnR的子集

MatnI={A∈MatnR|l(ξ)A?l(ξ)}

是MatnR的子環，且l(ξ)是MatnI的理想．

.

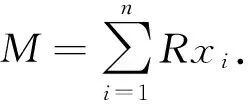
定理4有限生成模RM的自同態環同構于矩陣環MatnR的子環的商環．

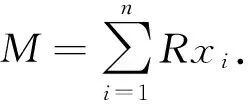
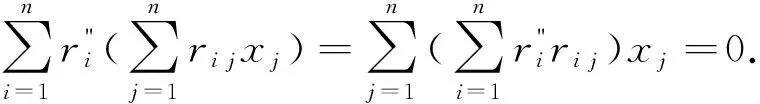
若f=f′，則(ri j)-(r′i j)=(ri j-r′i j)∈l(ξ)，即(ri j)+l(ξ)=(r′i j)+l(ξ)．所以，φ是End(RM)到MatnI/l(ξ)的一個映射．

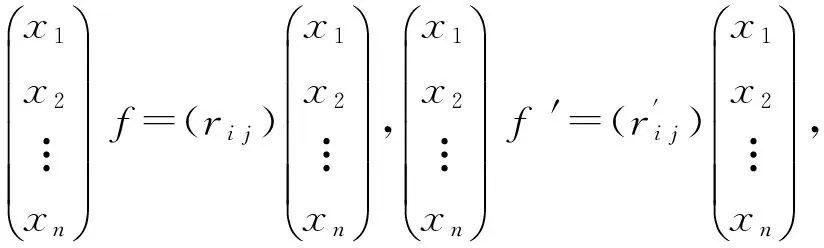
從而φ(f+f′)=φ(f)+φ(f′)．又因為

即φ(ff′)=φ(f)φ(f′),所以，φ是End(RM)到MatnI/l(ξ)的環同態．

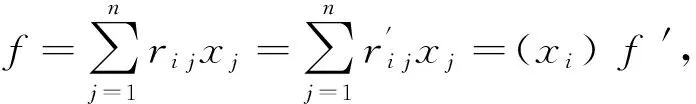
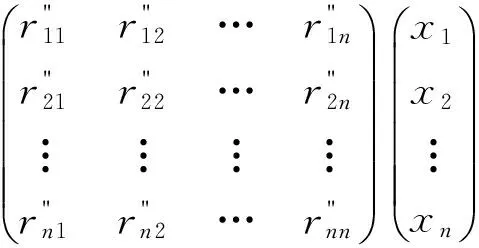
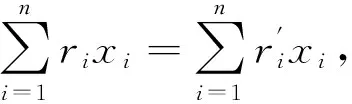
因為(r"i j)∈MatnI，所以

從而

當RM是循環模時，R上的1×1矩陣環顯然同構于R，此時定義1中的零化子與定義2中所定義的零化子一致，即定理1可視為定理4的特例．

推論3n維自由模RM的自同態環同構于矩陣環MatnR．

證明 當RM是n維自由模，且取x1,…,xn是RM的基時，定理4中的l(ξ)=0，MatnI=MatnR．證畢．

線性代數中熟知的域k上的向量空間的自同態環同構于k上n×n矩陣環，亦可看作推論3的特例．

[1]Drensky V,Szigeti J,van Wyk L.Centralizers in endomorphism rings[J].J Algebra,2010,324(12):3378-3387.

[4]Goldie A,Small L W.A note on rings of endomorphisms[J].J Algebra,1973,24(2):392-395.

[5]Anderson F W,Fuller K R.Rings and categories of modules[M].2nd ed.New York:Springer-Verlag,1992.

[6]陳晉健,陳順卿.模論[M].鄭州:河南大學出版社,1994.

(責任編輯 陶立方)

Acharacterizationofendomorphismringsoffinitelygeneratedmodules

WANG Feifei, ZHENG Qingyue, ZHAO Yanbo, CHEN Miaosen

(CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,JinhuaZhejiang321004,China)

It was defined annihilators of matrix rings and characterized endomorphism rings of finitely generated modules. The endomorphism ring of a finitely generated leftR-module was proved to be the homomorphic image of a subring of the matrix ring overR, and a new proof to some classical results in algebra was given.

annihilator; finitely generated module; endomorphism ring; matrix ring

O153

A

1001-5051(2013)02-0150-05

2013-01-05

國家大學生創新創業活動計劃資助項目(201210345010)

王飛飛(1989-)，男，浙江杭州人，碩士研究生.研究方向：代數學.

陳淼森. E-mail: mschen@zjnu.cn