不變子空間方法及一個非線性演化方程的精確解*

姜丙利， 柳銀萍

(華東師范大學 計算機科學與技術系，上海 200241)

不變子空間方法及一個非線性演化方程的精確解*

姜丙利， 柳銀萍

(華東師范大學 計算機科學與技術系，上海 200241)

應用不變子空間方法構造了一個非線性演化方程的精確解，通過分別考慮其2階和3階不同的不變子空間，獲得了3個具有分離變量形式的精確解.通過和已有的解比較，所得的解都是首次報道的新解.

不變子空間方法；精確解；非線性演化方程；廣義變量分離

0 引 言

非線性演化方程精確解對研究自然界的各種非線性運動具有重要意義，因為這些解可幫助人們洞察運動系統內部的結構，從而獲得更廣泛的應用.不變子空間方法是構造非線性偏微分方程精確解的有效方法之一，最早是由Titov等[1-2]提出，后經Qu Changzheng等[3]進一步優化和拓展，使得該方法能應用于求解兩耦合的非線性演化方程的精確解.該方法通過不同階的不變子空間，可以獲得不同形式的精確解[4-6].文獻[7]還給出了兩耦合的非線性演化方程可能擁有的最大不變子空間的維數估算；文獻[8]將該估算一般化，給出了由多個方程組成的方程組可能擁有的最大不變子空間的維數估算；文獻[9-10]在前人工作的基礎上，進一步簡化了該方法的應用.

本文基于文獻[9-10]的工作，應用不變子空間方法求解了一個非線性演化方程.

1 不變子空間方法的基本思路

考慮一個非線性演化方程

式(1)中:

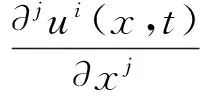
式(2)中:mi表示第i個非線性微分算子Fi的最高階微分次數;Fi[u]是足夠光滑的非線性微分算子.

應用不變子空間法的具體步驟如下：

步驟1 確定非線性演化方程的不變子空間.

令Wk1,k2,…,kq表示線性空間W1k1×W2k2×…×Wqkq，其中

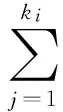
要求對任意的1≤i≤q,fi1(x),fi2(x),…,fiki(x)都是線性無關的.不妨令Wiki表示一個ni階線性微分方程解的子空間，即

式(5)中:ni≥ki;ai0(x),ai1(x),…,aini-1(x)是連續函數.

如果矢量微分算子F滿足如下條件：

也就是

那么，稱F有不變子空間Wk1,k2,…,kq.

步驟2 構造非線性演化方程的精確解.

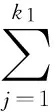
非線性演化方程的不變子空間是Wk1,k2,…,kq,當且僅當Cij(t)滿足

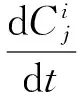
方程(1)具有如下形式的精確解[9-10]：

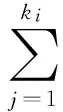
求解線性微分方程(10)，結合式(11)，即可得到非線性演化方程(1)的精確解.

2 應用不變子空間方法求解一個非線性演化方程

考慮非線性演化方程[11]

式(12)中:p,q,r是常數；F[u]是非線性微分算子.根據文獻[7-8]的結論，通過計算知，方程(12)所能考慮的不變子空間的最高維數為5，并且其他階的不變子空間沒有非平凡解.因此，以下僅分別考慮在2階和3階不變子空間來構造該方程的精確解.

2.12階不變子空間W2

2階不變子空間W2由如下線性微分方程定義：

式(13)中，a0,a1是待定常數.故方程(12)的不變子空間為W2的不變條件為

將F代入方程(14)，反復用-a1ux-a0u替代uxx,整理得到含有項uq+1,uxuq,u2xuq-1,u3xuq-2和u4xuq-3的方程.令方程中不同項的系數為零，則得到方程組

應用吳消元法軟件包Charsets[12-13]求解代數方程組(15)，得到2組非平凡解：

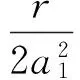
將式(16)和式(17)分別代入式(12)和式(13)，得到

2.23階不變子空間W3

3階不變子空間W3由如下線性微分方程定義：

式(20)中，a0,a1,a2是待定常數.故方程(12)的不變子空間為W3的不變條件為

同樣地，將非線性算子F代入方程(21)，反復用-a2uxx-a1ux-a0u替代uxxx,整理得到含有項uq+1,uxuq,uxxuq,u3xuq-2,u2xuq-1,u4xuq-3,u5xuq-4,u2xxuq-1,uxuxxuq-1,u2xuxxuq-2,u3xuxxuq-3和uxu2xxuq-2的方程.令方程中不同項的系數為零，于是有方程組

應用吳消元法軟件包Charsets求解代數方程組,可得

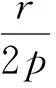
將式(23)代入式(12)和式(20)，得

綜上所述，通過分別考慮2階和3階不同的不變子空間，獲得了3個不同的系統,即系統(18)、系統(19)和系統(24).下面將基于這3個系統構造方程(12)的精確解.

2.3構造精確解

例1考慮非線性系統(18)，由式(16)可知，系統(18)中的非線性方程是方程(12)在q=2時的情形，即

其相應的2階不變子空間W2為

由L[y]=0可得方程(25)的不變子空間為

令方程(25)有如下形式的精確解：

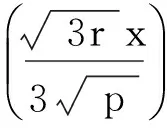
將式(28)代入方程(25)，有

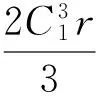
求解方程(29)，可得

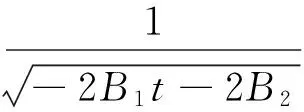
式(30)中，B1,B2是任意常數.由式(28)和式(30)可得方程(25)的精確解為

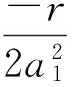
其相應的2階不變子空間W2為

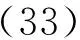
由L[y]=0可得方程(32)的不變子空間為

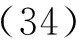
令方程(32)有如下形式的精確解：

將式(35)代入方程(32)，得

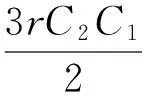
求解方程(36)，得到

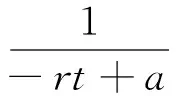
因此，由式(35)和式(37)可得方程(32)的精確解為

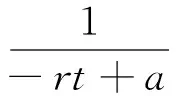
例3考慮非線性系統(24)，由式(23)可知，系統(24)中的非線性方程是方程(12)在q=1時的情形，即

其相應的3階不變子空間W3為

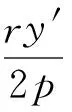
由L[y]=0可得方程(39)的不變子空間為

令方程(39)有如下形式的精確解：

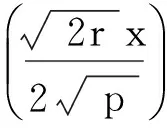
將式(42)代入方程(39)，有

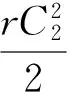
求解方程(43)得到

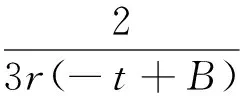
式(44)中，B是任意常數.由式(42)和式(44)可得方程(39)的精確解為

3 結 論

不變子空間方法是構造非線性演化方程精確解的有效方法之一，本文將不變子空間方法應用到一個具有未知參數指數的非線性演化方程，通過分別考慮其2階和3階不同的不變子空間，分別獲得了未知參數分別滿足不同約束條件時的不同形式的精確解.這些解與文獻[11]中已知的分離變量形式的解具有不同的結構，它們都是首次報道的新解.

[1]Titov S S.A method of finite-dimensional rings for solving nonlinear equations of mathematical physics[C]//Ivanova T P.Aerodynamics.Saratov:Saratov University,1988:104-109.

[2]Galaktionov V A.Invariant subspaces and new explicit solutions to evolution equations with quadratic nonlinearities[J].Proc Roy Soc Endin Sect A,1995,125(2):225-246.

[3]Qu Changzheng,Zhu Chunrong.Classification of coupled systems with two-component nonlinear diffusion equations by the invariant subspace method[J].Journal of Physics A:Mathematical and Theoretical,2009,42(47):475201.

[4]Galaktionov V A,Svirshchevskii S R.Exact solutions and invariant subspaces of nonlinear partial differential equations in mechanics and physics[M].London:Chapman and Hall/CRC,2007.

[5]King J R.Exact polynomial solutions to some nonlinear diffusion equations[J].Physica D：Nonlinear Phenomena,1993,64(1/2/3):35-65.

[6]Svirshchevskii S R.Lie-backlund symmetries of linear ODEs and generalized separation of variables in nonlinear equations[J].Physics Letters A,1995,199(5/6):344-348.

[7]Zhu Chunrong,Qu Changzheng.Maximal dimension of invariant subspaces admitted by nonlinear vector differential operators[J].J Math Phys,2011,52(4):043507.

[8]Shen Shoufeng,Qu Changzheng,Jin Yongyang,el al.Maximal dimension of invariant subspaces to systems of nonlinear evolution equations[J].Chinese Annals of Mathematics-Series B,2012,33(2):161-178.

[9]Ma Wenxiu.A refined invariant subspace method and applications to evolution equations[J].Science China Mathematics,2012,55(9):1769-1778.

[10]Ma Wenxiu,Liu Yinping.Invariant subspaces and exact solutions of a class of dispersive evolution equations[J].Communications in Nonlinear Science and Numerical Simulation,2012,17(10):3795-3801.

[11]Andrei D P,Valentin F Z.Handbook of nonlinear partial differential equations[M].London:Chapman & Hall/CRC,2004:52.

[12]Wang Dongming.An implementation of the characteristic set method in maple[M]//Pfalzgraf J,Wang Dongming.Automated practical reasoning:Algebraic approaches.New York:Springer-Verlag,1995:187-201.

[13]Wang Dongming.Elimination practice:Software tools and applications[M].London:Imperial College Press,2004.

(責任編輯 陶立方)

Theinvariantsubspacemethodandexactsolutionsforanonlinearevolutionequation

JIANG Bingli, LIU Yinping

(DepartmentofComputerScienceandTechnology,EastChinaNormalUniversity,Shanghai200241,China)

The invariant subspace method was applied to construct exact solutions of a nonlinear evolution equation, and three solutions in the form of separation of variables were successfully obtained with the help of different invariant subspaces. Compared with known solutions, these solutions were first reported new solutions.

invariant subspace method; exact solution; nonlinear evolution equation; separation of variables

O157.5

A

1001-5051(2013)02-0155-06

2012-11-09

國家自然科學基金資助項目(11071274)

姜丙利(1987-),男,山西長治人,碩士研究生.研究方向:符號計算;數學機械化.

柳銀萍.Email： ypliu@cs.ecnu.edu.cn