展開法求解變系數KP方程的精確解*

郭冠平

(浙江師范大學 教師教育學院,浙江 金華 321004)

郭冠平

(浙江師范大學 教師教育學院,浙江 金華 321004)

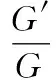
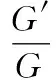
0 引 言

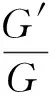
的解.可以看出,這種方法直接且有一般性，適合于處理這類非線性演化方程.

1 變系數KP方程的精確解

對于方程(1)，設

并設式(1)有如下的解:

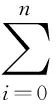
式(3)中,G=G(ξ)滿足如下二階線性常微分方程(LODE)：

式(4)中,Ai(i=0,1,…,n),λ,μ是待定的常數；n由齊次平衡法(平衡最高階導數項和非線性項)確定.

由齊次平衡法可知，n=2，所以式(3)變為

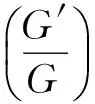
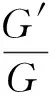
以上各式中,ρ=120f2A2ξ4x+60f1A22ξ2x.

從式(6)中可以求得

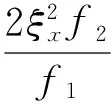
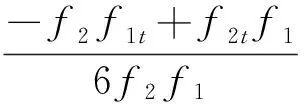
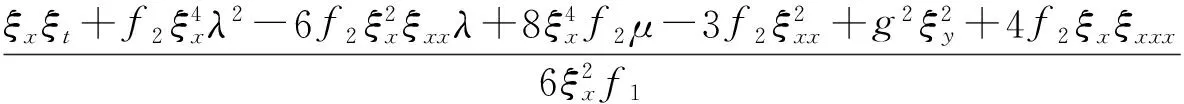
(15)

把式(13)～式(15)代入式(5)，得

當λ2-4μ>0,λ2-4μ<0,λ2-4μ=0時，分別可以得到雙曲函數形式解、三角函數形式解和有理函數形式解.限于篇幅，本文只討論λ2-4μ>0的情況,其中:

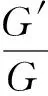
把式(17)代入式(16)，可得式(1)的新精確解.其中C1,C2是任意常數.

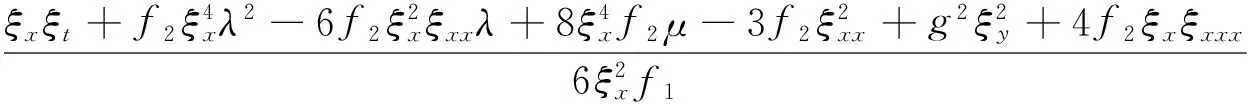
(18)

特別地，取C1=0,C2≠0時,得到孤波解為

特別地，取C2=0,C1≠0時,得到孤波解為

若取ξ=kx+by+ct+ξ0,其中:k,b,c,ξ0為任意常數，則式(18)～式(20)分別變為行波解

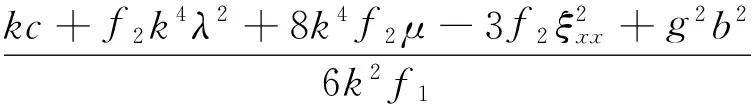
(23)

2 結 語

[1]Wang Mingliang.The solitary wave solutions for the variant Boussinesq equations[J].Physics Letters A,1995,199(3/4):169-172.

[2]張解放.長水波近似方程的多孤子解[J].物理學報,1998,47(9):1416-1420.

[3]范恩貴,張鴻慶.非線性孤子方程的齊次平衡法[J].物理學報,1998,47(3):353-361.

[4]王明亮,李志斌,周宇斌.齊次平衡原則及其應用[J].蘭州大學學報:自然科學版,1999,35(3):8-16.

[5]鄭贇，張鴻慶.一個非線性方程的顯式行波解[J].物理學報,2000,49(3):389-391.

[6]閆振亞,張鴻慶,范恩貴.一類非線性演化方程新的顯式行波解[J].物理學報,1999,48(1):1-5.

[7]張桂戍,李志斌,段一士.非線性方程的精確孤立波解[J].中國科學:A輯 數學,2000,30(12):1103-1108.

[8]郭冠平,張解放.關于雙曲函數方法求孤波解的注記[J].物理學報,2002,51(6):1159-1162.

[9]郭冠平,張解放.長短波相互作用方程的Jacobi橢圓函數求解[J].物理學報,2003,52(11):2660-2663.

[10]郭冠平,張解放.非可積(3+1)維KdV型方程的一類多孤子解[J].西安石油學院學報,2002,17(3):82-84.

[11]劉式適,傅遵濤,劉式達,等.Jacobi橢圓函數展開法及其在求解非線性波動方程中的應用[J].物理學報,2001,50(11):2068-2073.

[12]套格圖桑，白玉梅.構造非線性發展方程無窮序列類孤子精確解的一種方法[J].物理學報,2012,61(13):130202.

[13]李幫慶,馬玉蘭.(G′/G)展開法和(2+1)維非對稱Nizhnik-Novikov-Veselov系統的新精確解[J].物理學報,2009,58(7):4373-4378.

[14]Zhu Zuonong.Painlevé property,B?cklund transformation,Lax pair and soliton-like solution for a varianble coefficient KP equation[J].Physics Letters A，1993，182(2/3):277-281.

(責任編輯 杜利民)

GUO Guanping

(CollegeofTeacherEducation,ZhejiangNormalUniversity,JinhuaZhejiang321004,China)

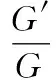
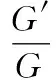
O340

A

1001-5051(2013)02-0166-06

2012-09-26

郭冠平(1960-)，男，浙江東陽人，副教授.研究方向：非線性物理.