具有半交換自同態的環

王 堯，沈 青，任艷麗

（1.南京信息工程大學 數學與統計學院，南京210044；2.南京曉莊學院 數學與信息技術學院，南京211171）

本文所討論的結合環均假設有單位元1，α是給定環R 的自同態，且滿足α（1）＝1.對任意的a，b∈R，如果ab＝0，有ba＝0，則稱環R是可逆環［1］.對任意的a，b，c∈R，如果abc＝0，有acb＝0，則稱環R是對稱環［1］.對任意的a，b∈R，如果ab＝0，有aRb＝0，則稱環R是半交換環［1］.對任意的a，b∈R，如果ab＝0，有bα（a）＝0（α（b）a＝0），則環R 稱為右（左）α－可逆的.對任何a，b∈R，如果ab＝0，有aRα（b）＝0（α（a）Rb＝0），則環R稱為（左）α－半交換環.對任意的a，b，c∈R，如果abc＝0，有acα（b）＝0（α（b）ac＝0），則稱環 R 是右（左）α－對稱的［2］.對任何a，b∈R，如果aα（b）＝0（α（a）b＝0），有bα（a）＝0（α（b）a＝0），則該環稱為右（左）α－shifting環.文獻［3－4］研究了α－可逆環和α－半交換環；文獻［5］研究了具有可逆自同態的環.本文研究具有半交換自同態的環（即α－sc環，它是半交換環概念的推廣），討論α－sc環和相關環的關系，并給出了α－sc環的一些擴張性質.

1 α－sc環與相關環

定義1 設α是環R 的自同態.對任何a，b∈R，如果α（a）b＝0（aα（b）＝0），有aRα（b）＝0（α（a）Rb＝0），則稱α是（左）半交換的.如果R有（左）半交換自同態α，則稱環R是（左）α－sc環.如果環R既是α－sc環又是左α－sc環，則稱R為雙邊α－sc環.

顯然，當α＝IdR時，單邊IdR－sc環是半交換環，其中IdR表示R的恒等同態.

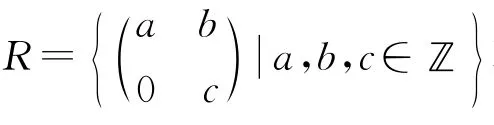
例1表明，當α≠IdR時，α－sc環未必是半交換環.

例2 1）令?2＝?／（2），考慮環R＝?2⊕?2和R 的自同構α：R→R，α（（a，b））＝（b，a）.由文獻［3］中例2.3知，R不是α－半交換環.對任何A＝（a，b），B＝（c，d）∈R，若α（A）B＝0，則ad＝0，bc＝0，于是有ACα（B）＝0，?C＝（m，n）∈R，故R是α－sc環.

2）考慮域F上的多項式環R＝F［x］和R的自同態α：R→R，α（f（x））＝f（0），f（x）∈R.由文獻［3］中例2.5（2）知，R 是α－半交換環.取f（x）＝x，g（x）＝a≠0，r（x）＝b≠0∈R，有α（f（x））g（x）＝0，但f（x）r（x）α（g（x））≠0，故R 不是α－sc環.

例2表明，α－半交換環與α－sc環也是相互獨立的概念.

命題1 設R是可逆環，α是環R的自同態，則R是α－sc環當且僅當R是左α－sc環.

證明：必要性.已知R是可逆環，對?a，b∈R，若aα（b）＝0，則α（b）a＝0.由R是α－sc環知bRα（a）＝0，bα（a）＝0.對?r∈R，rbα（a）＝0，從而α（a）rb＝0，故R是左α－sc環.

充分性.已知R是可逆環，對?a，b∈R，若α（a）b＝0，則bα（a）＝0.由R是左α－sc環知α（b）Ra＝0，α（b）a＝0，對?r∈R，α（b）ar＝0，從而arα（b）＝0，故R是α－sc環.

對任何a∈R，若aα（a）＝0，有a＝0，則環R稱為α－rigid環［6］.由文獻［7］中命題5知α－rigid環是約化環（半交換環）；由文獻［3］中定理2.4知每個α－rigid環都是α－半交換環，但反之不成立.

命題2 設α是環R的自同態，則下列結論等價：

1）R是α－rigid環；

2）R是α－sc環，且由aRα（a）＝0可推出a＝0，?a∈R；

3）R是左α－sc環，且由α（a）Ra＝0可推出a＝0，?a∈R.

證明：1）?2）.對a，b∈R，若α（a）b＝0，則α（ba）ba＝0.由R 是α－rigid環知ba＝0，于是aα（b）α（aα（b））＝aα（ba）α2（b）＝0，從而aα（b）＝0.由α－rigid環是半交換環可得aRα（b）＝0，故R 是α－sc環.另一方面，對任意的a∈R，若aRα（a）＝0，則aα（a）＝0，再由R是α－rigid環知a＝0.

2）?1）.已知2）成立，對?a∈R，若α（a）a＝0，由R是α－sc環知aRα（a）＝0.根據已知條件有a＝0，故R是α－rigid環.

1）?3）.類似可證.

推論1［1］環R是約化環當且僅當R是半素環和半交換環.

證明：令α＝IdR，根據命題2可得.

命題2中2）的條件“aRα（a）＝0可推出a＝0，?a∈R”不是多余的.事實上，例2中1）R是α－sc環，但對0≠a＝（1，0）∈R有aRα（a）＝0，R不是α－rigid環.

定理1 設α是環R的自同態，則下列結論成立：

1）如果R是α－sc環，則α是環R的單同態；

2）如果α2＝IdR，則R是α－sc環當且僅當R是半交換環；

3）如果α是環R的單同態，R是半交換環和α－半交換環，則R是α－sc環.

證明：1）對?a，b∈R，設α（a）＝α（b），α（a－b）＝0，由R 是α－sc環知，（a－b）Rα（1）＝0，（a－b）α（1）＝0，從而a＝b，故α是單同態.

2）必要性.對?a，b∈R，設ab＝0，則α（ab）＝α（a）α（b）＝0.由R是α－sc環知aRα2（b）＝0，于是aRb＝0，因此R是半交換環.

充分性.對?a，b∈R，設α（a）b＝0，則α（α（a）b）＝α2（a）α（b）＝aα（b）＝0，由R 是半交換環知aRα（b）＝0，故R是α－sc環.

3）設α（a）b＝0，?a，b∈R，由于R是α－半交換環，故α（a）Rα（b）＝0，α（a）α（b）＝0，從而

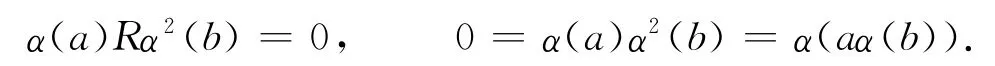
由α是單同態知aα（b）＝0，故aRα（b）＝0，因此R是α－sc環.

命題3 設R是可逆環，α是環R的自同態，則下列結論等價：

1）R是α－sc環；

2）對R 中的任意非空子集B，α（rR（α（B）））?rR（B）；

3）?r∈R，α（rR（α（r）））?rR（r）；

4）對R中的任意非空子集A，B，α（A）B＝｛0｝?ARα（B）＝｛0｝.

證明：1）?2）.已知R是α－sc環，對a∈α（rR（α（B））），有c∈R，使得a＝α（c），α（B）c＝0.于是對任何b∈B，有α（b）c＝0.由R是α－sc環知bRα（c）＝0，即bRa＝0，從而有ba＝0.所以a∈rR（B），于是α（rR（α（B）））?rR（B）.

2）?3）和4）?1）顯然成立.

定理2 設α是環R的自同態，則下列結論成立：

1）如果R是α－sc環，且α（e）＝e，e2＝e∈R，則R和R［x；α］都是Abel環；

2）如果R［x；α］是可逆環，則R是雙邊α－sc環.

證明：1）若α（e）＝e，e2＝e∈R，則有α（e）（1－e）＝0，α（1－e）e＝0.由R是α－sc環知

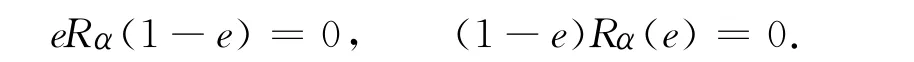
于是對任何r∈R，有er（1－e）＝0，（1－e）re＝0，即er＝ere＝re，表明R是 Abel環.由文獻［5］定理2.9中（1）知R［x；α］也是 Abel環.

2）對?a，b∈R，如果aα（b）＝0，取p（x）＝ax，q（x）＝bx∈R［x；α］，則有p（x）q（x）＝aα（b）x2＝0.由R［x；α］是可逆環知q（x）p（x）＝bα（a）x2＝0，因此bα（a）＝0，rbα（a）＝0，?r∈R.從而由R 是可逆環知α（a）rb＝0，因此R是左α－sc環.又由命題1知R是α－sc環.

命題4 約化的α－Armendariz環是雙邊α－sc環.

證明：由文獻［8］知約化的α－Armendariz環是α－rigid環，又由命題2知α－rigid環是雙邊α－sc環.

命題5 設α是環R的自同態.如果由aRα（a）＝0可推出a＝0，?a∈R，則下列結論等價：

1）R是約化的α－Armendariz環；

2）R是雙邊α－sc環；

3）R 是（左）α－sc環；

4）R是α－rigid環；

5）R［x；α］是約化環；

6）R是約化環.

證明：1）?2）.由命題4可知.2）?3）和5）?6）顯然.3）?4）由命題2即得.4）?5）由文獻［9］中命題3可知.4）?1）由文獻［7］中命題6可得.6）?4）由文獻［5］中命題2.12可得.

命題6 設R是約化環，則R是右α－shifting環當且僅當R是α－sc環.

證明：必要性.對?a，b∈R，設α（a）b＝0，由R是約化環知bα（a）＝0.對?r∈R，bα（a）α（r）＝bα（ar）＝0.由于R是右α－shifting環，有arα（b）＝0，故R是α－sc環.

充分性.對?a，b∈R，設aα（b）＝0，則α（b）a＝0.因為R是α－sc環，所以bRα（a）＝0，bα（a）＝0，故R是右α－shifting環.

2 α－sc環的擴張

設α是環R 的一個自同態，I是R 的一個子環（理想）.如果α（I）?I，則稱I為R 的α－子環（理想）.

命題7 設R是環，α是環R的自同態，則下列結論成立：

1）α－sc環的任意α－子環也是α－sc環；

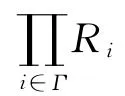
給定環R和雙模RMR，R通過M 的平凡擴張定義為T（R，M）＝R⊕M，其運算是通常的加法和如下的乘法：

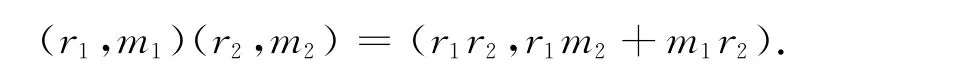
命題8 設α是約化環R的自同態.如果R是α－sc環，則T（R，R）也是環.

推論2［10］設R是約化環，則T（R，R）是半交換環.

命題9 設R是約化環，α是環R的自同態.如果R是α－sc環，則S3（R）也是環.

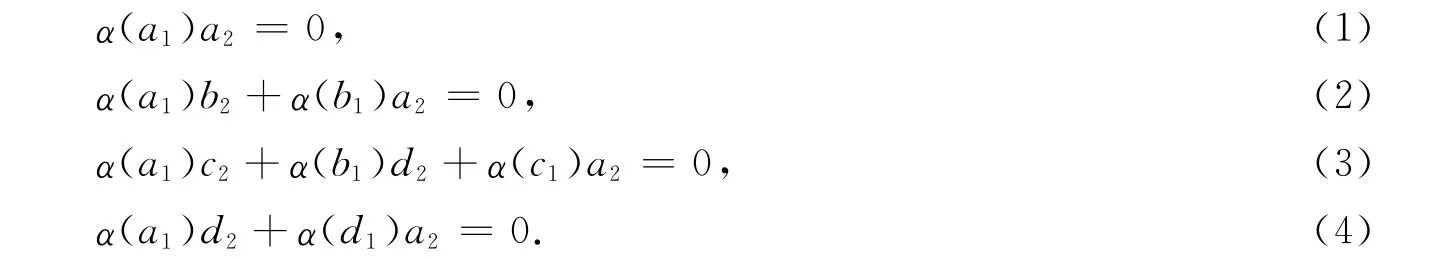
已知R是約化環，由式（1）知a2α（a1）＝0.由式（2）可得

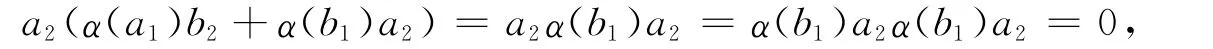
于是α（b1）a2＝0，α（a1）b2＝0.同理，由式（4）可得α（a1）d2＝0，α（d1）a2＝0.再由式（3）可得

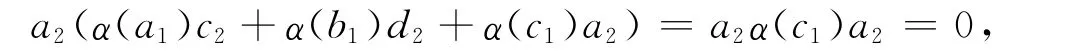
從而α（c1）a2＝0，α（a1）c2＋α（b1）d2＝0.又因為

故α（a1）c2＝0，α（b1）d2＝0.已知R 是α－sc環，有

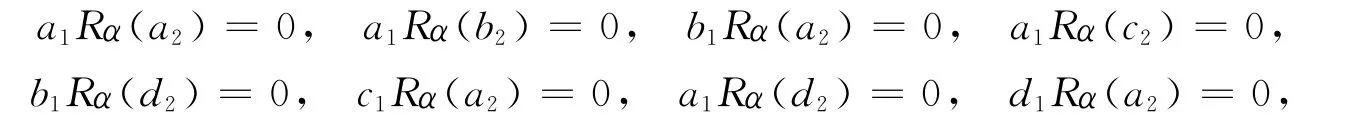
推論3［1］設R是約化環，則S3（R）是半交換環.

命題10 設R是Armendariz環，α是環R的自同態，則下列結論等價：

1）R是α－sc環；

2）?1）顯然.

命題11 設α是環R的自同態，則下列結論成立：

1）如果R是可逆環，I是R的α－rigid理想，R／I是環，則R是α－sc環；

2）如果對R的任何中心冪等元e有α（e）＝e，則eR和（1－e）R是環當且僅當R是環.

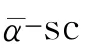
2）充分性.根據命題7中（1）可知.

必要性.已知eR和（1－e）R是ˉα－sc環，對?a，b∈R，若α（a）b＝0，則有

于是有

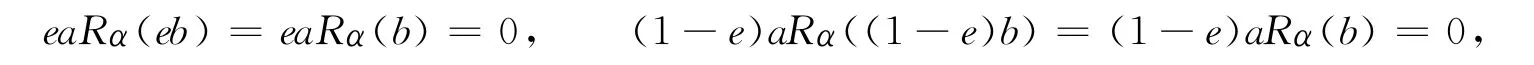
因此

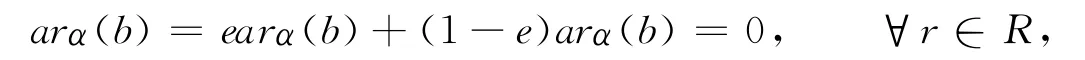
即R是α－sc環.

定理3 設α是約化環R的自同態，則R是α－sc環當且僅當R［x］／〈xn〉是環，其中〈xn〉是由xn生成的理想，n為任何正整數.

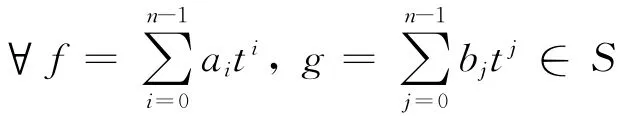
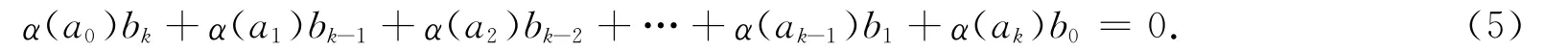
將式（5）左乘α（α（b0））得α（α（b0）ak）b0＝0.由R 是α－sc環知

由R是約化環知α（b0）ak＝0，因為R 是α－sc環，所以b0Rα（ak）＝0，b0α（ak）＝0，從而α（ak）b0＝0，akRα（b0）＝0.于是，式（5）可變為

將式（6）左乘α（α（b1））同理可得α（ak－1）b1＝0，ak－1Rα（b1）＝0.于是式（6）可變為

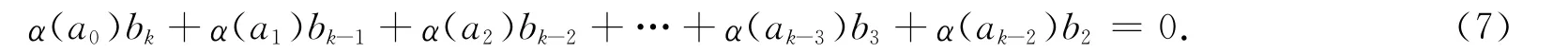
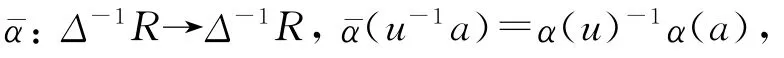
命題12 設α是環R的自同構，如果Δ是由R的中心正則元構成的乘法封閉子集，且α（Δ）?Δ，則R是α－sc環當且僅當Δ－1R是環.

證明：充分性.根據命題7中（1）可知.

于是α（a）b＝0.由R是α－sc環知aRα（b）＝0.對任何C＝w－1c∈Δ－1R，其中c∈R，w∈Δ，有

即Δ－1R是環.

推論4 設α是環R的自同態，則R［x］是環當且僅當R［x；x－1］是環.

證明：設Δ＝｛1，x，x2，…｝，則Δ是由R［x］的中心正則元構成的乘法封閉子集，R［x；x－1］＝Δ－1R［x］，由命題12即得結論.

定理4 設α是環R的自同構，R是對稱的右Ore環，Q（R）是R的經典右商環，則R是α－sc環當且僅當Q（R）是環.

證明：充分性.根據命題7中（1）可知.

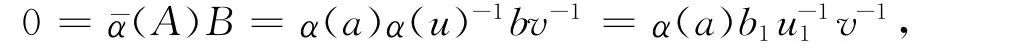
從而α（a）b1＝0.由R是對稱環知

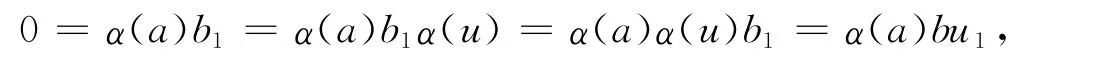
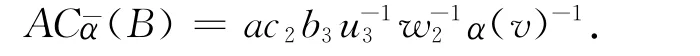
于是，對?c∈R，有

從而

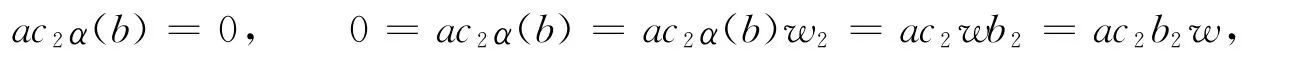
進而

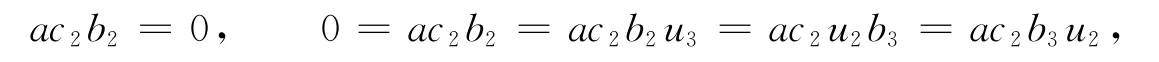
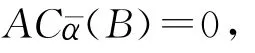
［1］Kim N K，Lee Y.Extensions of Reversible Rings［J］.J Pure Appl Algebra，2003，185（1／2／3）：207－223.

［2］Kwak T K.Extensions of Extended Symmetric Rings［J］.Bull Korean Math Soc，2007，44（4）：777－788.

［3］Baser M，Hong C Y，Kwak T K.On Extended Reversible Rings［J］.Algebra Colloq，2009，16（1）：37－48.

［4］Baser M，Harmanci A，Kwak T K.Generalized Semicommutative Rings and Their Extensions［J］.Bull Korean Math Soc，2008，45（2）：285－297.

［5］Baser M，Kaynarca F，Kwak T K.Ring Endomorphisms with the Reversible Condition［J］.Commun Korean Math Soc，2010，25（3）：349－364.

［6］Krempa J.Some Examples of Reduced Rings［J］.Algebra Colloq，1996，3（4）：289－300.

［7］Hong C Y，Kim N K，Kwak T K.Ore Extensions of Baer and PP－Rings［J］.J Pure Appl Algebra，2000，151（3）：215－226.

［8］Hong C Y，Kwak T K，Rizvi S T.Extensions of Generalized Armendariz Rings［J］.Algebra Colloq，2006，13（2）：253－266.

［9］Hong C Y，Kim N K，Kwak T K.On Skew Armendariz Rings［J］.Comm Algebra，2003，31（1）：103－122.

［10］GANG Yang.Semicommutative and Reduced Rings［J］.Vietnam J Math，2007，35（3）：309－315.