線性互補問題解的存在性

楊泰山，姜興武，王秀玉

（1.吉林大學 數學學院，長春130012；2.吉林工商學院 基礎部，長春130062；3.長春工業大學 基礎科學學院，長春130012）

線性互補問題是：求x≥0，使得y＝Mx＋q≥0且有xTy＝0，其中M為一個n階方陣，該互補問題記為LCP（M，q），稱為非齊次互補問題.當q＝0時，記為LCP（M，0），稱為齊次互補問題.線性互補問題是互補問題的一個重要組成部分，并且二次規劃的K－K－T方程也為線性互補問題.

同倫方法由于具有大范圍收斂性，目前已成為求解數學問題的一個重要工具.文獻［1］構造了一類同倫方程求解互補問題；文獻［2－6］對文獻［1］的同倫方程給出了不同條件下同倫路徑的存在性；文獻［7］建立了與文獻［1］完全不同的同倫方程，獲得了互補問題的可解性，但文獻［7］的同倫方程當參數為零時不能回到原互補問題，也未給出具體條件；文獻［8］改進了文獻［7］的結果，利用同倫方法對互補問題進行求解.本文運用文獻［1］的同倫方程給出半單調線性互補問題同倫路徑的存在性、有界性及收斂性，并給出LCP（M，q）有解與LCP（M，0）只有零解的關系.

本文用x≥0或x∈?n＋（x＞0或x∈?n＋＋）表示向量x的每個分量為非負（正數），用w＝（x，y）表示向量w＝（xT，yT）T.

1 預備知識

定義1［9］如果對任意的x≥0，x≠0，存在一個分量xk＞0，使得（Mx）k≥0，則n階方陣M∈?n×n稱為半單調矩陣.

當M為半單調矩陣時，互補問題LCP（M，q）稱為半單調線性互補問題.

假設條件：

（H1）M∈?n×n是半單調矩陣；

（H2）y＝Mx，x≥0，y≥0，xTy＝0只有零解；

（H3）存在u∈?n＋＋，使得v＝Mu＋q＞0；

（H4）存在常數τ≥0，α≥0，1＜β＜2，使得對任意的x∈?n，y∈?n，下式成立：

例1

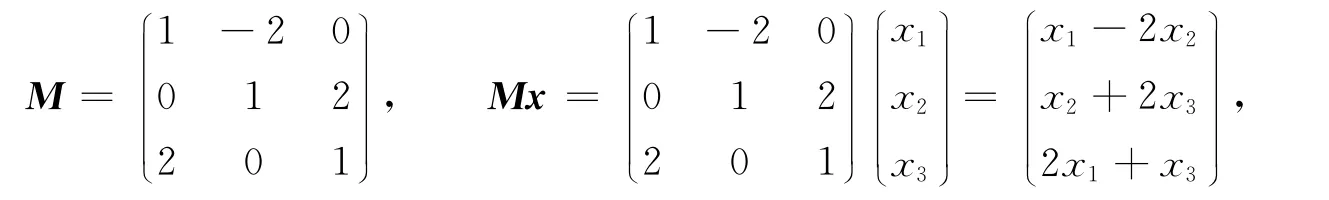
則M顯然為半單調矩陣.令

則M不是P0矩陣.

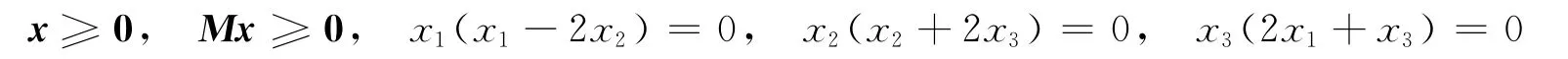
只有零解.M 滿足假設條件（H1），（H2）.

2 主要結果

記w＝（x，y），任取x（0）＞0，y（0）＞0及w＝（x（0），y（0）），構造如下同倫方程：

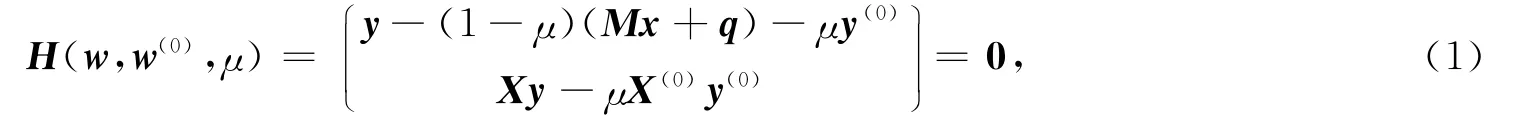
其中X＝diag（x）.同倫方程（1）也記為Hw（0）（w，μ），并記

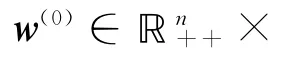
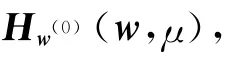
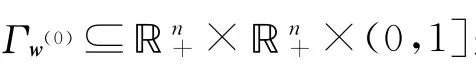
證明：Γw（0）的存在性由定理1可得.Γw（0）??n＋×?n＋×（0，1］顯然成立.若Γw（0）無界，則必存在子列（x（k），y（k），μk）∈Γw（0），使得當k→∞時，有‖（x（k），y（k），μk）‖→∞，由同倫方程（1）的第二個等式得

由式（2）可知

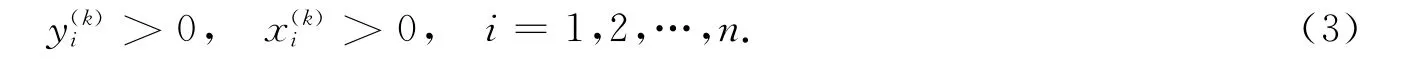
由同倫方程（1）的第一個等式得

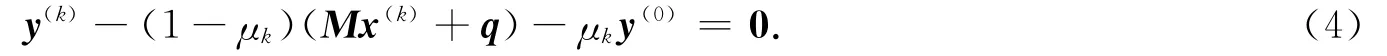
情形1）μ＊∈［0，1）.

由式（2）及x（＊），y（＊）的定義，對任意的i＝1，2，…，n，得

又由式（6）知（x（＊），y（＊））為齊次互補問題LCP（M，0）的非零解，與假設（H2）矛盾.

情形2）μ＊＝1.分兩種情形論證.

令

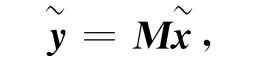
而由式（2）可知，對任意的i＝1，2，…，n，有

因而由式（2），（9）得

式（10）與｛x（k）｝無界性矛盾.

式（4）兩邊取極限得

再由式（2）得

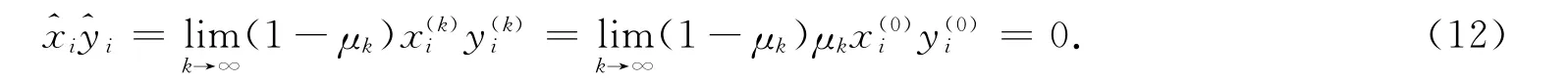
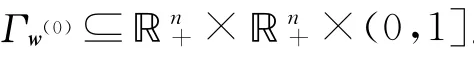
由式（4）－式（13），得

將式（2）代入式（14）的分量形式，對所有的i＝1，2，…，n，得

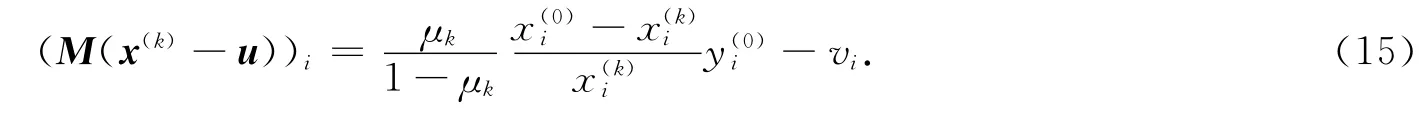
由式（15）可知

由式（16）可知，當x（k）i→∞時，有

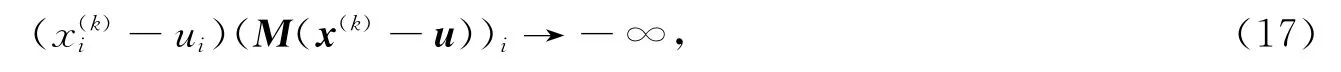
且對所有的i＝1，2，…，n，有

由于｛x（k）｝為無窮序列，因而存在整數s，p，使得

顯然有

由式（18），（19）可知，對充分大的k，有

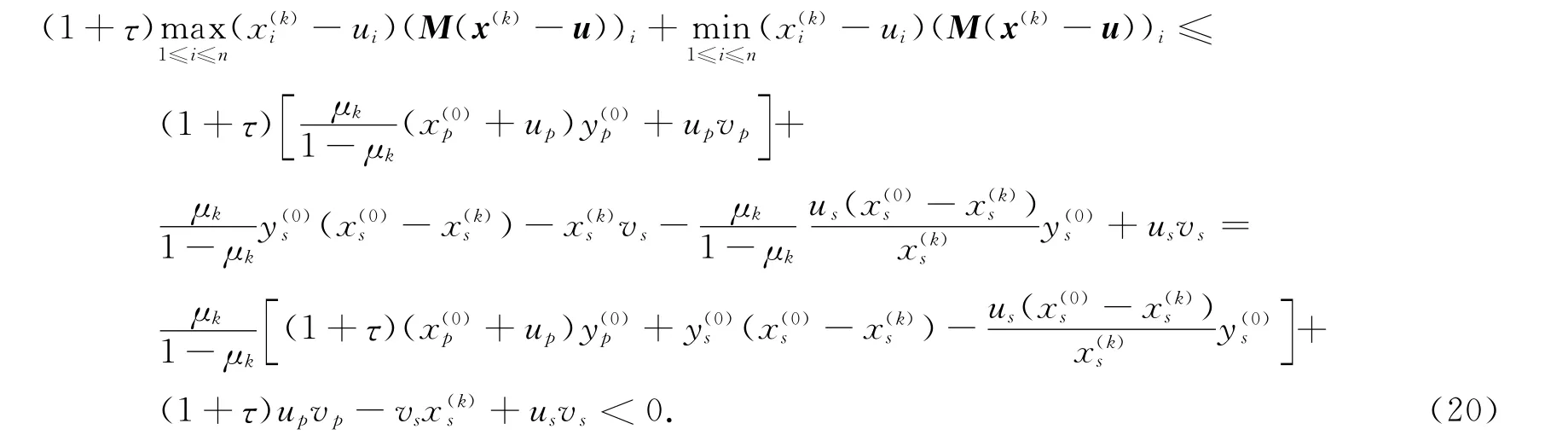
由條件（H3）知下式成立：

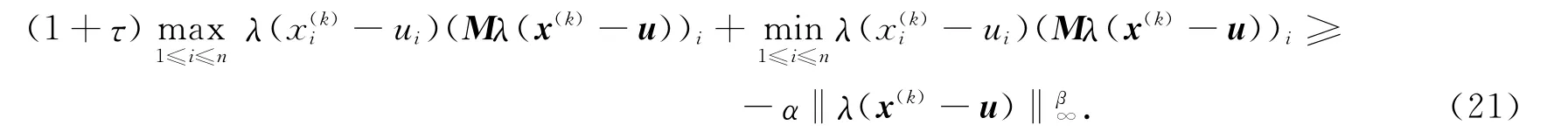
整理式（21）得

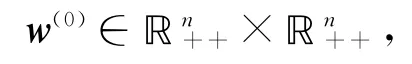
證明：由定理1～定理3易知Γw（0）為有界曲線.由一維流形分類定理知，Γw（0）微分同胚于單位圓周或單位區間（0，1］（證明與文獻［7］的定理2.1類似）.注意到

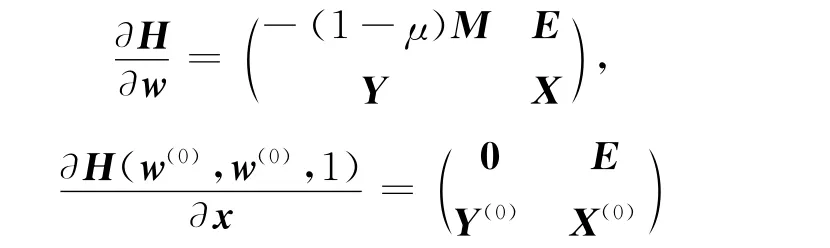
是非奇異的，得Γw（0）不能微分同胚于單位圓周，而只能微分同胚于單位區間.記（w（＊），μ＊）為Γw（0）的極限點，則只有下列4種情形可能發生：

［1］Kojima M，Megiddo N，Mizuno M.A General Framework of Continuation Methods for Complementarity Problems［J］.Math Oper Res，1993，18（4）：945－963.

［2］XU Qing，DANG Chang－yin.A New Homotopy Method for Solving Non－linear Complementarity Problems［J］.Optimization，2008，57：681－689.

［3］YU Qian，HUANG Chong－chao，WANG Xian－jia.A Combined Homotopy Interior Point Method for the Linear Complementarity Problem ［J］.Applied Mathematics and Computation，2006，179（2）：696－701.

［4］ZHAO Yun－bin，LI Gong－nong.Properties of a Homotopy Solution Path for Complementarity Problems with Quasi－monotone Mappings［J］.Applied Mathematics and Computation，2004，148：93－104.

［5］LI Gong－nong.Analysis for a Homotopy Path of Complementarity Problems Based onμ－Exceptional Family［J］.Applied Mathematics and Computation，2005，169（1）：657－670.

［6］WANG Xiu－yu，JIANG Xing－wu， LIU Qing－huai.The Combined Homotopy Method for Nonlinear Complementarity Problems［J］.Acta Mathematicae Applicatae Sinica，2012，35（3）：430－440.（王秀玉，姜興武，劉慶懷.非線性互補問題的組合同倫算法 ［J］.應用數學學報，2012，35（3）：430－440.）

［7］DING Jun－di，YIN Hong－you.A New Homotopy Method for Nonlinear Complementarity Problems ［J］.Numericla Mathematics，A Journal of Chinese Universities：English Series，2007，16（2）：155－163.

［8］WANG Xiu－yu， JIANG Xing－wu， LIU Qing－huai.New Homotopy Method for Solving Nonlinear Complementarity Problems［J］.Journal of Jilin University：Science Edition，2012，50（3）：494－498.（王秀玉，姜興武，劉慶懷.求解互補問題的新同倫算法 ［J］.吉林大學學報：理學版，2012，50（3）：494－498.）

［9］韓繼業，修乃華，戚厚鐸.非線性互補理論與算法 ［M］.上海：上海科學技術出版社，2006.