非自治強阻尼梁方程的漸近行為

任永華，張建文

（太原理工大學 數學學院，太原 030024）

眾所周知，非線性發展方程領域中系統的漸近行為自然地由相應的半群的吸引子來描述[1-6]。其中，對系統吸引子的研究一直受到眾多數學物理學工作者的高度關注。宋雪麗等證明了具有非線性耗散項的三維Navier-Stokes方程強解整體吸引子的存在性[3]；而 Simsen Jacson和 Simsen Mariza Stefanello討論了p（x）-拉普拉斯微分方程組的漸近行為[4]。當系統明顯地依賴于時間t時，情況變得相當復雜，由于非自治系統中受到的與時間有關的外力作用破壞了自治系統所產生的半群性質，那些在自治系統中發揮重要技術的關鍵理論不再適用，需要進一步推廣。目前，非自治系統已經取得了相當的進展，文獻[5]研究了非自治弦方程的吸引子，但對于非自治梁方程的一致吸引子的研究相對較少。本文著重考慮如下非自治強阻尼梁系統在空間E＝V×H中的一致吸引子的存在性：

其中k≥0，u＝u（x，t）是關于變量x和t的Ω×[τ，＋∞）的算子函數。Ω?Rn（n∈N）是一個有界開集，且具有充分光滑的邊界Γ.h＝h（x，t）∈Η（h0）與時間相關，且在（R，L2（Ω））上是平移緊的。這里，我們設

1 解的存在唯一性

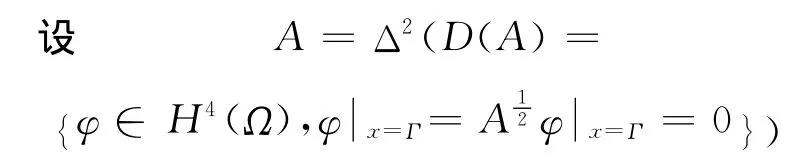
是一個自伴正定線性算子，并具有特征值｛λi｝i∈N滿足0＜λ1≤λ2≤ … ≤λm…，λm→＋∞（m→＋∞）；

分別表示H＝L2（Ω），和V＝H20（Ω）上的內積和范數。

下面考慮系統（1）-（3）.為了證明解的存在性，我們假設

其中?s1，s2∈R，C1，C2為非負常數，｜·｜0為 R上數的絕對值。

其中?s∈R，β1，β2為常數。

這樣我們容易將系統（1）-（3）簡化為關于時間的一階抽象發展方程。令?u／?t＝v，系統等價于Hilbert空間E上的初值問題：

由文獻[1，2]知，C是一個扇形算子，且是E中解析半群eCt的無窮小生成元。由參考文獻[6]，易知N（U，t）在E上是全局Lipschitz連續的。再由微分方程的解的存在唯一性理論，有如下定理。

定理1 假設條件（H1）、（H2）成立，則對于任意的Uτ∈E，存在唯一的函數U（·，Uτ）∈C（（τ，＋∞），E），使得Uτ＝U（τ，Uτ）且U（t）滿足下面的積分方程

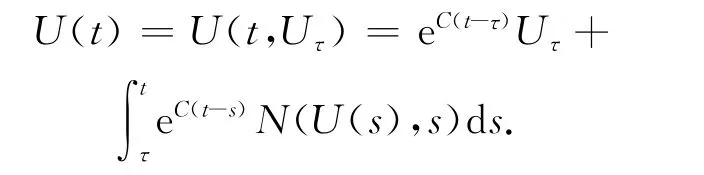
U（t，Uτ）關于t和Uτ共同連續，且?T＊＞0，

2 一致吸引子的存在性

分別表示E＝V×H上的內積和范數。

引理1 對于?φ＝（u，v）T，有

根據Gronwall不等式，在空間（E，｜·｜E）中，得到下面的吸收不等式：

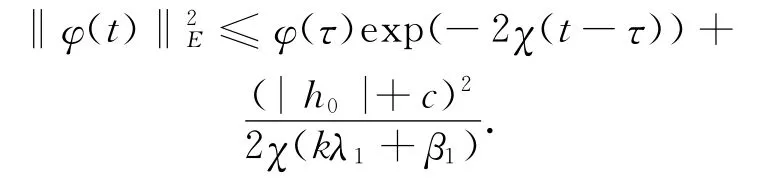
據上，可得出下面引理。

引理3 對應于問題（6）的過程族｛Sh（t，τ）｝，h∈H（h0）有一個一致有界的吸收集B0.也就是說，吸收集

是一致吸收的；則，對于所有的h∈Η（h0）和對于E的任意的有界集B，對于t≥τ＋t1（B），Sh（t，τ）B?B0成立。

引理4 對應于問題（6）的過程族｛Sh（t，τ）｝，h∈Η（h0）是一致漸近緊的，和（E×H（h0），E）-連續的。

證明 設φ（t）＝（u（t），v（t））T是問題（6）的解。初值分別為φ1τ和φ2τ的（6）的兩個解φ1（t）和φ2（t）.它們的差φ＝φ1-φ2滿足

用φ對式（11）做內積（·，·）E，得

下面我們逐項估計。

因此，對于?t≥τ，過程族｛Sh（t，τ）｝，h∈Η（h0）是（E×H（h0），E）-連續的。從而，由上述引理結合定理1可得如下定理。

定理2 由問題（6）所定義的算子半群在空間E中具有一致吸引子。

[1]陳雙全，周盛凡，李紅艷.黏彈性和熱黏彈性方程的全局吸引子[J].應用數學與計算數學學報，2008，22（1）：14-20.

[2]姜金平，侯延仁，王小霞.含線性阻尼的2D-非自治g-Navier-Stokes方程的拉回吸引子[J].應用數學和力學，2011，32（2）：144-157.

[3]Song Xueli，Hou Yanren.Attractors for the three-dimensional incompressible Navier-Stokes equations with damping[J].Discrete and Continuous Dynamical Systems，2011，31（1）：239-252.

[4]Simsen Jacson，Simsen Mariza Stefanello.Existence and upper semicontinuity of global attractors for p（x）-Laplacian systems[J].J Math Anal Appl，2012，388（1）：23-38.

[5]Wan Li，Zhou Qinghua.Attractor and boundedness for stochastic Cohen-Grossberg neural networks with delays[J].Neurocomputing，2012，79：164-167.

[6]Temam R.Infinite-Dimensional Dynamical Systems in Mechanics and Physics[M].New York：Springer，1988.