恒電流刺激下神經元Chay模型的Hopf分岔分析

李洪明，張素麗

（1.呼倫貝爾學院 數學系，內蒙古 呼倫貝爾 021008；2.太原理工大學 數學學院，太原 030024）

1 Chay模型的概述

20世紀50年代Hodgkin和Huxley首次提出了經典Hodgkin-Huxley模型[1]（簡稱 H-H模型），該方程主要研究神經元細胞的放電行為。但是HodGkin和Huxley主要考慮的是神經軸突膜中的K＋和Na＋通道離子電流，因而不能全面描述神經元細胞的膜電壓特性。1994年，Chay等人通過大量實驗，在H-H模型的基礎上提出Chay模型[2]。Chay模型除了考慮可興奮細胞膜上Na＋和K＋通道及漏電流通道的作用外，還有賴于Ca2＋濃度的K＋離子通道，后者對于依賴Ca2＋的各類肌細胞和胰島B細胞的放電是極重要的。因此神經元Chay模型能更好地模擬神經元的各種放電形式。

古華光等主要研究了Chay模型的兩類躍遷機制產生的整數倍神經放電節律[3-7]；崔睿等研究了三態躍進機制產生的兩種放電節律[8]；張春燕等進行了神經元典型放電的計算機仿真[9]；裴利軍等進行了神經元Chay模型的動力學分析[10]；陸啟韶等對神經元Chay模型的生理特性進行了深入的詳細研究[12-14]。本文主要利用非線性動力學方法對Chay模型進行了單參數的Hopf分岔分析，然后證明了其Hopf分岔的存在性。

Chay模型可用下面的三階非線性微分方程表示[2]：

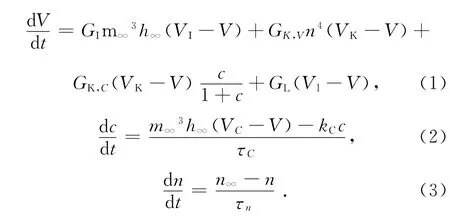
方程（1）描述了神經元細胞的膜電位的變化規律；VI，VK，VL，V 分別表示 Na＋-Ca2＋通道、K＋通道、漏電流的電位和平衡電位；GI，GK，V，GK，C，GL分別代表各通道的最大電導；c為細胞內Ca2＋濃度；n為K＋通道開放概率；m∞，h∞分別是Ca2＋、Na＋通道門打開的概率。

方程（2）描述了細胞膜內Ca2＋變化規律。VC是Ca2＋可逆電位；τc為常量，τc＝100／27；kC表示Ca2＋流出細胞內的速率常數。

方程（3）描述了K＋通道門打開概率的變化規律。τn是弛豫時間常數；n∞為K＋通道門打開的概率。

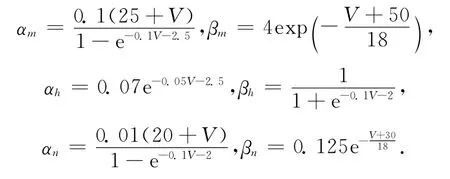
由文獻[2]知，m∞，n∞，h∞分別是Ca2＋、K＋和Na＋離子通道門打開的概率，為

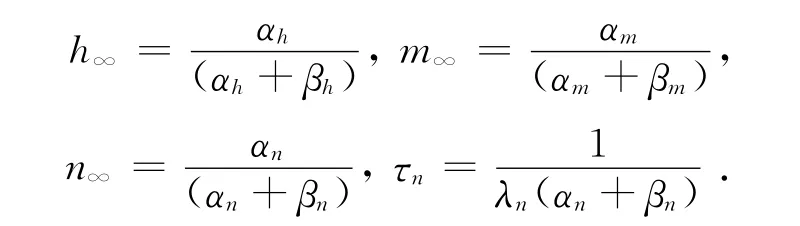
本文中參數取值如下：GI＝1800S；GK，V＝1700S；GL＝7S；VI＝100mV ；VK＝-75mV；VL＝-40mV；V＝100mV

2 Chay模型的平衡點及其穩定性

對于方程（1）、（2）、（3）所示的自治系統，設其平衡點為A（Ve，ce，ne），令方程（1）（2）（3）右端等于0，即

由式（5）、（6）可知：

則ne，ce均為Ve的函數。將ne，ce代入（4）得：

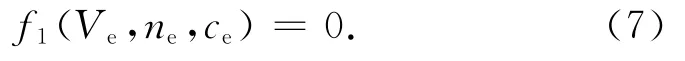
數值計算發現，式（7）僅有一個解，得平衡點為

Chay模型在該點處的Jacobian矩陣為

其相應的特征根為

根據穩定性理論[11]，由于平衡點的特征根有正實部，可以判定平衡點A（Ve，ce，ne）為不穩定的點。

3 恒電流刺激下神經元Chay模型的Hopf分岔分析

恒電流刺激下Chay模型可用下面的三階非線性微分方程表示：

式中，I為恒流電流。

設恒電流刺激下系統的平衡點為B（Ve，ce，ne），模型參數取已給出的值，改變I的值，通過數值計算方法求解，得到如表2所示。

表1 其他參數不變，只改變I時，Chay模型的唯一平衡點 B（Ve，ce，ne）的坐標、特征根及其穩定性

恒電流刺激下神經元Chay模型在平衡點B（Ve，ce，ne）處的Jacobian矩陣為J（B），數值計算得到系統在I取不同值時的特征值，如表1所示。前三種情況，即I分別為-65，-66，-66.6μA／cm2時，均存在正實部特征根，根據穩定性理論[11]，可以判定平衡點B（Ve，ce，ne）為不穩定的結點。后2種情況，即I分別為-66.7，-66.8，-67μA／cm2時，其特征根為一對共軛復根與一實根，且共軛復根的實部與實根都為負，則可判定其為漸進穩定的結點。

4 數值模擬

以上的理論計算得到的分岔情況只反映了參數變化引起的系統穩態解的變化。為了全面考察參數對模型的動態特性的影響，下面用Matlab軟件進行了參數連續變化下的數值模擬。圖1、2、3驗證了當I＝-65，I＝-66，I＝-66.6μA／cm2時，神經纖維產生周期性動作電位，Chay模型出現穩定周期解。

圖4、5顯示了當I通過-66.6μA／cm2時，在其附近發生Hopf分岔，其跨膜電壓經小幅衰減振蕩后穩定在略高于穩定點的某一平衡點，周期解消失，可以看到，隨著I的增大，當越過臨界值時，系統出現漸進穩定平衡點，振蕩消失。

圖1 I＝65μA／cm2時膜電位V隨時間t的變化

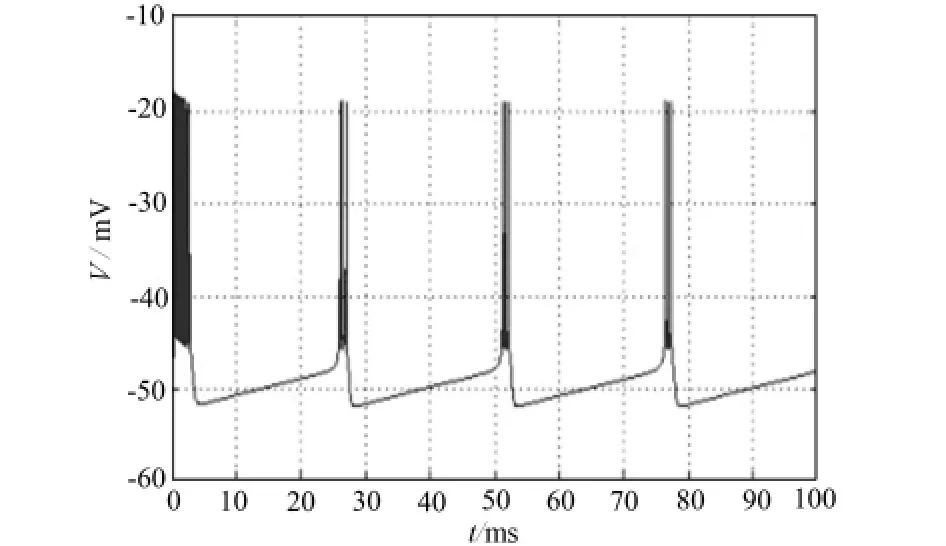
圖2 I＝-66μA／cm2時膜電位V隨時間t的變化

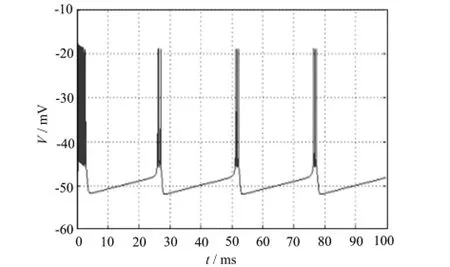
圖3 I＝-66.6μA／cm2時膜電位V隨時間t的變化

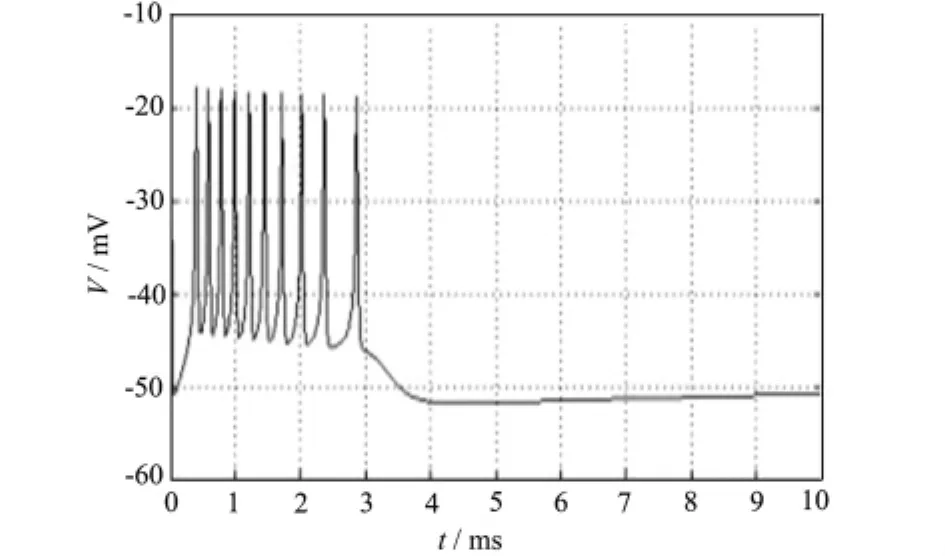
圖4 I＝-66.7μA／cm2時膜電位V隨時間t的變化

圖5 I＝-67μA／cm2時膜電位V隨時間t的變化

5 結束語

本文僅對恒電流刺激下神經元Chay模型的Hopf分岔進行了分析，與實際生理系統中多因素的共同作用有較大差別，因此還需進一步的對全局分岔和多層次分岔結構進行研究。此外，實際神經系統中的神經元總是受到內外噪聲、參數的微小漲落等影響。因此，我們需考慮更多的隨機因素的作用。

[1]Hodgkin A L，Huxley A F.A quantitative description of membrane current and its application to conduction and excitation in nerve[J].J Physiol，1952，117：500-544.

[2]Chay T R.Chaos in three variable model of an excitable cell[J].Physica D，1985，16（2）：233-242.

[3]楊明浩，古華光，李莉，等.神經放電加周期分岔中由隨機自共振引起的一類新節律[J].生物物理學報，2004，20（6）：465-470.

[4]古華光，李莉，楊明浩，等.實驗性神經起步點產生的整數倍簇放電節律[J].生物物理學報，2003，20（1）：68-72.

[5]古華光，任維，楊明浩，等.神經自發整數倍峰放電節律的隨機性和確定性模式的比較[J].生物物理學報，2003，19（3）：272-278.

[6]古華光，任維，陸啟韶，等.實驗性神經起步點自發放電的分叉和整數倍節律[J].生物物理學報，2001，17（4）：637-644.

[7]Gu HG，Ren W，Lu QS，et al.Integer multiple spiking in neuronal pacemakers without external periodic stimulation[J].Phys Lett A，2001，285：63-68.

[8]崔睿，王珊珊，李晉，等.由三態躍進機制產生的兩種神經放電節律[J].生物物理學報，2011，27（8）：703-711.

[9]張春燕，田心.可興奮神經元典型放電的計算機仿真[J].天津醫科大學學報，2004，（s1）

[10]裴利軍，王永剛，范燁.神經元Chay模型的動力學分析[J].鄭州大學學報（理學版），2009，2（41）：7-12.

[11]馬知恩，周義倉.常微分方程定性與穩定性方法[M].北京：科學出版社，2001：41-92.

[12]Duan LX，Lu QS.Codimension-two bifurcation analysis on firing activities in Chay neuron model[J].Chaos，Solitions and Fracials，2006，30（5）：1172-1179.

[13]Yang ZQ，Lu QS.Transitions from bursting to spiking due to depolarizing current in the Chay neuronal model[J].Communications in Nonlinear Science and Numerical Simulation，2007，12（3）：357-365.

[14]Duan LX，Lu QS，Wang QY.Two-parameter bifurcation analysis of firing activities in the Chay neuronal model[J].Neurocomputer，2008，72（1-3）：341-351