直埋供熱管道“L”形管段的受力分析

劉楨彬，王 飛，王國偉，雷勇剛

（太原理工大學 環境科學與工程學院，太原 030024）

熱力管道直埋敷設方式在城市集中供熱建設中得到大量應用，而彎頭是直埋供熱管道中的重要構件，對直埋供熱管道的安全運行起著極其重要的作用。設計中，彎頭應力是驗算的重點，其峰值應力產生的疲勞破壞是彎頭破壞的主要形式[1]。

目前，驗算彎頭疲勞強度的主要計算方法是彈性抗彎鉸法和有限元法，工程上主要按《城鎮直埋供熱管道工程技術規程》（CJJ／T 81-98）中的彈性抗彎鉸法計算。該規程適用于公稱直徑小于或等于500mm的預制保溫直埋熱水管道，且該規程在強度計算、管道熱伸長計算當中對荷載作了簡化處理，對小管徑管道影響不大；但當管徑逐漸增大以后，簡化計算結果會產生較大偏差，這是不安全的。目前工程中的管徑已達1200mm，設計大管徑直埋管道時主要依據文獻[1]，該文獻在驗算彎頭疲勞強度時使用的仍是規程中所使用的彈性抗彎鉸解析法，摩擦系數參考太原熱力設計院與太原理工大學在2001-2003年的合作實驗結果[2]。

有限單元法是當今公認的一種用數值方法求解工程中所遇到的各種問題的最有效的方法（各種力學問題、聲問題等），它是通過對連續問題進行有限數目的單元離散來近似的，是分析復雜結構和復雜問題的一種強有力的分析工具。然而，目前僅有少數文獻使用ANSYS軟件對直埋供熱管道進行過數值模擬分析，且建模方法及其可靠性沒有詳盡的說明。文獻[3]中用位移荷載替代溫度荷載，但是彎頭處的自由端膨脹量是與土壤反力相互耦合的[4]，文獻[3]中的有限元分析并沒有模擬這種耦合作用。

筆者給出一種較為完整的有限元建模方法，施加了位移、土壤摩擦力、彎頭附近土壤反力、內壓及溫度荷載，并將模擬結果與彈性抗彎鉸解析法相比較，以期對此種建模方法的可靠性進行考核，為DN500以上的大管徑供熱管道受力分析提供建模支持和參考。

1 荷載的分類[5]

在直埋敷設供熱管道重力作用面內，重力屬于力荷載，而土壤的支撐作用屬于位移荷載。由于土壤的均勻支撐，這兩種荷載在這個垂直平面內并沒有產生很大的彎曲應力，所以在進行力學計算時，可忽略這兩種荷載作用。另外，作用于直埋管道表面上的土壓力，與管道內介質壓力相比很小，管道的內外壓差作用可以只考慮管道內部介質壓力作用。因此，在直埋敷設供熱管道應力分析和受力計算中只考慮下列荷載：

1）力荷載，由內壓力引起的荷載，由土壤摩擦力產生的荷載；

2）位移荷載，固定墩位移產生的荷載；

3）力-位移荷載，由力和位移共同作用產生的荷載，補償器的彈力、側向壓縮反力引起的荷載；

4）溫度荷載，輸送熱水產生的溫度荷載。

2 建立模型

2.1 計算的假設條件

管道受力的計算是以管材是彈性的、連續的、均勻的和各向同性的作為假設前提，忽略管道壁厚不均勻度和橢圓度（不考慮橢圓度更加安全[6]）。直埋敷設供熱管道受固定墩的位移荷載、土壤摩擦力、彎頭附近土壤反力、內壓及溫度的作用。

2.2 管道尺寸及材料特性

取臂長為40m的等臂直角“L”形管段，材料為Q235鋼，管材彈性模量取19.6×104MPa，線性膨脹系數12.6×10-6m／（m·℃），泊松比0.3；管徑由DN150到DN500，彎頭內外徑、保溫管外徑及曲率半徑見表1，直管與彎頭內外徑及保溫厚度相同。管內介質為熱水，循環工作溫差取120℃，壓力為1.6MPa。

表1 管道型號及其尺寸一覽表

2.3 模型的簡化

由于在僅考慮固定墩的位移荷載、土壤摩擦力、彎頭附近土壤反力、內壓及溫度作用的條件下，“L”形管段在垂直方向上的荷載具有對稱性，為節省計算時間，建模時僅建立垂直方向上的下半個模型。為模擬彎頭附近的土壤反力作用，在管道的垂直對稱面上，離管道一定距離的外圍位置創建面模型支撐面。在面與管道間創建彈簧來模擬彎頭附近的土壤反力，如圖1所示。忽略彎頭處的土壤摩擦力，直管上的土壤摩擦力以施加在節點上的力來模擬。

3 ANSYS有限元分析

模擬結果分兩組分析，一組不施加內壓荷載，一組施加內壓荷載。繪制位移圖像、SINT應力圖及SEQV應力圖，并點取彎頭中部在直管軸線方向的最大位移以及彎頭處的SINT及SEQV最大值，與彈性抗彎鉸法計算的理論值作對比分析。圖2是模擬管道在有內壓時Z方向的位移圖，模擬管道在有內壓時的SINT受力最大值位于彎頭的頂部，其值為833.68MPa。圖3為繪制的管道SINT受力圖。圖2、圖3顯示時隱藏了彈簧及其附著面。

圖1 ANSYS模型單元圖

圖2 DN300管道有內壓時Z方向的位移圖

圖3 ANSYS管道有內壓時的SINT受力圖

4 彈性抗彎鉸法

4.1 理論簡化

在分析中將彎頭的幾何尺寸略去不計，而保留它的抗彎柔性，將它簡化成能夠傳遞彎矩的鉸鏈模型，稱為“彈性抗彎鉸”。彈性抗彎鉸法在描寫側向土壤反力時，采用了與管道橫向位移成比例的假定，同時還假定土壤摩擦力沿軸向均勻分布。

4.2 理論公式

本文理論計算采用的經簡化后所得到的對稱情況（L1＝L2＝L）下的橫向位移曲線（y（x））及彎頭端彎矩（M）公式，其表達式如下：

y（x）代表直管x處熱脹時的橫向位移；L為管道臂長；E為彈性模量；J為直管和彎頭的截面慣性矩；α為線性膨脹系數；t為管道升溫值；F為直管橫截面積；q為管道的單長摩擦力；φ為轉角管段的折角；c為側向土壤壓縮反力系數；K為彎頭柔性系數[7]。考慮管道內壓對熱內力的影響時，在以上諸表達式中，按文獻[7]中方法修正。直埋彎頭在彎矩作用下的最大環向應力按下式計算：

綜合最大應力按下式計算[8]：

式中：λ為彎頭的尺寸系數；rbo為彎頭的外半徑；pd為管道的計算壓力；Dbi為彎頭內徑；δb為彎頭的公稱壁厚。

5 結果分析

位移與受力模擬分析結果與理論計算結果對比見表2所示。圖4為無內壓和有內壓端面位移理論值與端面位移模擬值的比較。圖5為彎頭頂部最大受力的理論計算值與模擬的有內壓最大SINT值和有內壓最大SEQV值的比較。由圖可知，模擬值與理論值吻合較好，可說明ANSYS模擬模型的建立方法與荷載施加方法正確。

表2 位移與受力結果對比表

圖4 端面位移的理論值與模擬值比較

端面位移模擬值y（40）與理論計算值、彎頭頂部無內壓受力的SINT最大值和有內壓受力的SINT最大值，與理論計算結果的偏差率見表3所示。可知，有內壓位移偏差與理論計算值在10%以內，其他偏差都在5%以內。對管道彎頭最大受力進行分析可知，有內壓時計算值比模擬的SINT值略小，比模擬值的SEQV值略大，說明理論計算值是介于模擬的第三強度當量應力值和第四強度當量應力值之間的。

圖5 彎頭頂部最大受力計算值與模擬值的比較

比較文獻[7]與規程發現，在計算彎頭的彎矩變化范圍時，規程的Fminlcm前少了系數0.5，參考一些相關文獻，發現計算公式都與文獻[7]一致。模擬的SINT值與按規程中不含0.5系數的M公式計算得到的理論值的偏差率見表4所示。對比表4與表3和表2發現，按規程中沒有0.5系數的公式計算得到的結果與模擬值相差較大，且偏向不安全，因此筆者認為，規程在該公式處遺漏了系數0.5。

表3 位移與受力的模擬值與理論計算值的偏差

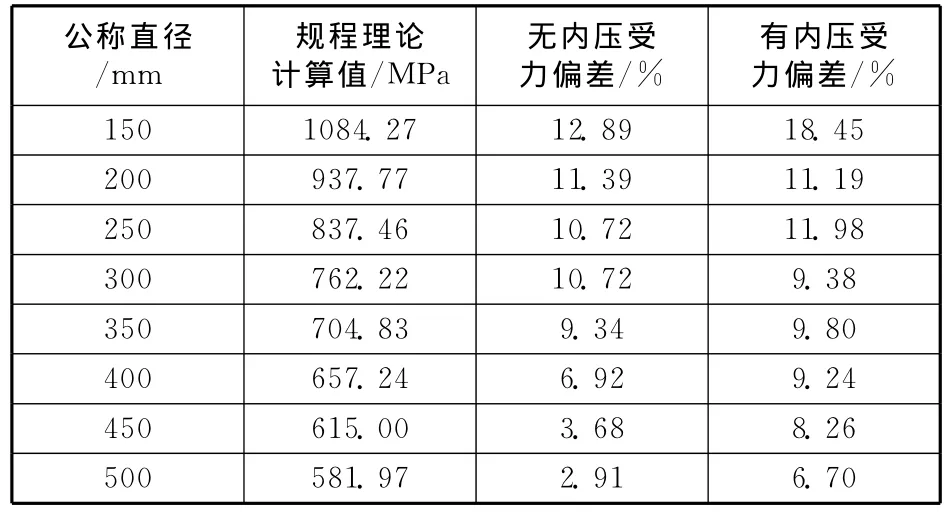
表4 彎頭受力模擬值與規程中公式的計算值偏差

6 結論

1）比較DN150—DN500管道的模擬值與彈性抗彎鉸方法的計算值發現，模擬值與理論值比較吻合，說明建模方法與荷載施加方法正確，可以根據此方法進行DN500以下管道的直埋問題研究，參考類似的建模與荷載施加方法，可進行DN500以上大管徑直埋管道的受力分析。

2）使用彈性抗彎鉸方法的理論計算值與模擬的理想彎頭在有壓時的受力值相比，理論值介于模擬值的第三強度理論當量應力和第四強度理論當量應力值之間。

3）規程中的Fminlcm前缺少0.5系數的公式計算的彎頭頂部受力值與模擬的理想彎頭的受力值相比，理論值偏差較大，且偏向危險方向，可見規程中公式遺漏了系數0.5。

[1]王飛，張建偉.直埋供熱管道工程設計[M].北京：中國建筑工業出版社，2006：2-4，70.

[2]張建偉，王飛，張貴成，等.大口徑預制直埋供熱管摩擦系數的研究[J].太原理工大學學報.2003，34（6）：703-706.

[3]王國偉.大口徑直埋供熱管道90°彎頭疲勞壽命的有限元分析[D].太原理工大學，2010.

[4]賀平，王鋼.區域供熱手冊[M].哈爾濱工程大學出版社，1998：98-99.

[5]劉偉.直埋敷設供熱管道應力分析與受力計算[D].哈爾濱，哈爾濱工程大學，2007.

[6]王飛，杜保存，王國偉.橢圓度對直埋供熱彎頭應力的影響[J].太原理工大學學報，2012，43（1）：83-85.

[7]崔孝秉.埋地長輸管道熱脹內力近似分析[J].力學學報，1984（01）：51-61.

[8]唐山市熱力總公司.CJJ／T 81-98城鎮直埋供熱管道工程技術規程[S].北京：中國建筑工業出版社，1999.