時變電磁場惟一性定理的一般證明及其物理解釋
孫春峰
(湖北工程學院 物理與電子信息工程學院,湖北 孝感432000)
麥克斯韋方程組是電磁場理論的核心內容,是分析電磁場問題的理論基礎。根據(jù)這組方程,可以建立實際電磁場初邊值問題的表達式,然后用某種方法求出該初邊值問題的解。惟一性定理是保證用不同的方法求解麥克斯韋方程組時都能得到同樣結果的理論依據(jù)。現(xiàn)行的電動力學教科書[1-3]和文獻[4-6]對于靜電邊值問題的惟一性定理和靜磁邊值問題的惟一性定理的證明討論較多,臻于完善。而對時變電磁場惟一性定理的證明涉及不多,有些教科書[7-8]雖有討論,但采用邊界上電磁場的零值強條件而不具一般意義;經(jīng)典的電磁場名著[9-10]討論了E?邊值或 H?邊值的邊界條件卻忽視了E?、H?邊值情況而存在局限。在時變電磁場情況下,解麥克斯韋方程組以求得時變電磁場的解,在什么樣的初始條件和邊界條件時才是麥克斯韋方程組解惟一性的最普遍條件?下面對此作些討論。
1 疊加解的初邊值問題
電磁場問題中,若只考察空間某一有限區(qū)域內的電磁場,而區(qū)域內外都存在場源時,除了由處于這個區(qū)域之內的源產(chǎn)生外,還可由這個區(qū)域之外的源產(chǎn)生。外部場源的影響反映在區(qū)域邊界處由外部源所形成的場值上,通過有限區(qū)域的邊界條件的作用實現(xiàn)。因此,有限區(qū)域的電磁場在已知內部場源初始時刻t0區(qū)域內任一點的電場、磁場之值和邊界上外部場源場值的條件下惟一確定。
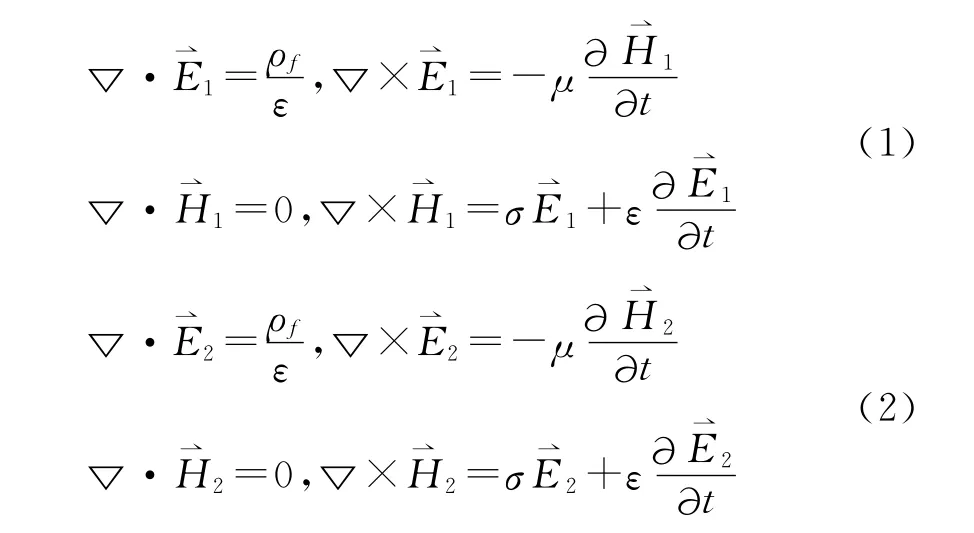
因為是同一場源電磁系統(tǒng),所以兩組方程中的源分布和電磁性質常數(shù)ε、μ、σ是相同的。同時,兩組方程中的解都滿足相同的初始條件和邊界條件。即在t=t0時
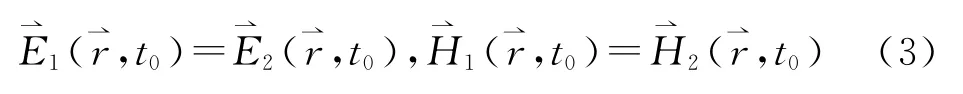
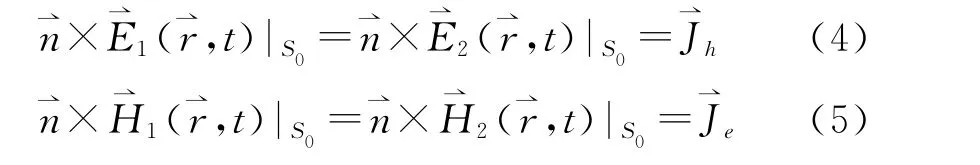
將方程(1)式和方程(2)式對應相減,并令
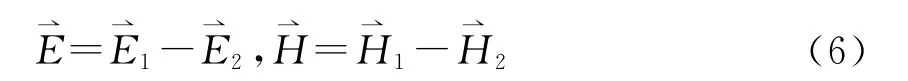
則疊加解(6)式滿足的方程組為
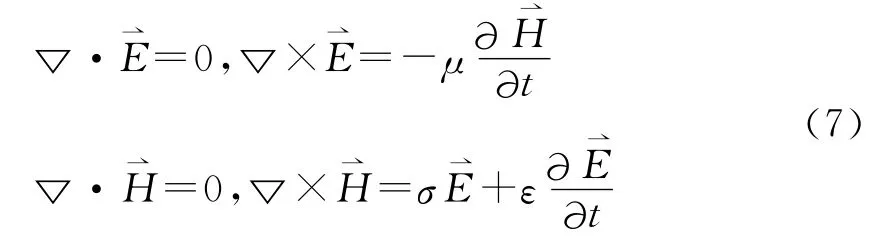
由(3)~(6)式得到方程組(7)式的初始條件和邊界條件為
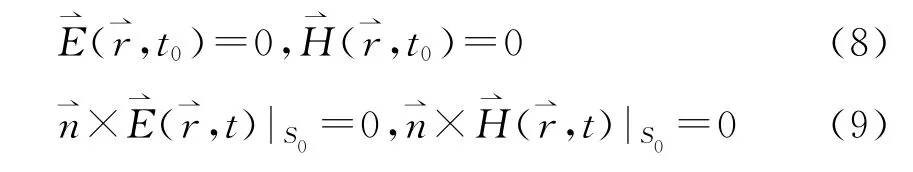
2 有限區(qū)域情形
假定區(qū)域V 中由V1,V2,…,Vm個子區(qū)域組成,分區(qū)均勻分布著線性介質,區(qū)域V的外邊界面為S0;V 內的公共界面分別為S1,S2,…,Sm,如圖1所示。每個子區(qū)域Vi,(i=1,2,…,m)中介質 的 電 磁 性 質 常 量εi,μi,σi均 為 大 于 零 的 實常數(shù)。
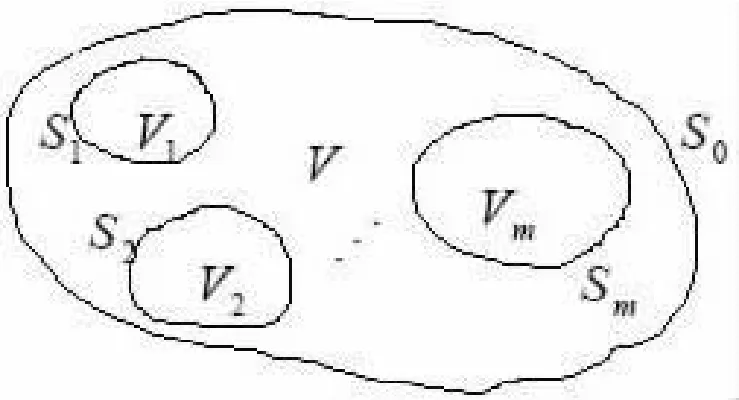
圖1 分區(qū)均勻的有限區(qū)域
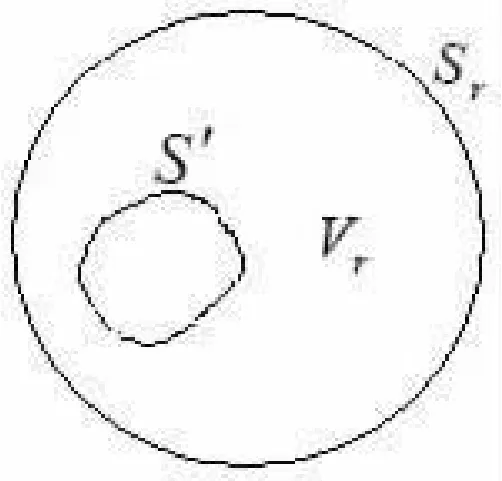
圖2 無限區(qū)域示意圖
設Vi中的電場強度為、磁場強度為則V中兩相鄰的介質區(qū)域Vi與Vj,其公共界面Sij上的邊值關系表為
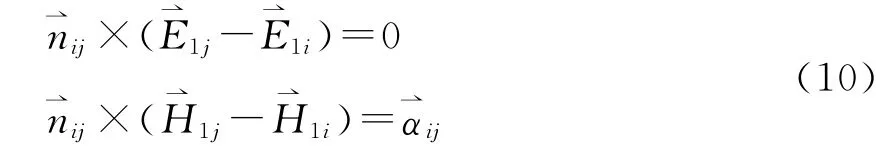
設Vi與Vj中的疊加解分別為與、則由(6)式和(10)式得到疊加解滿足的子區(qū)域邊界條件為
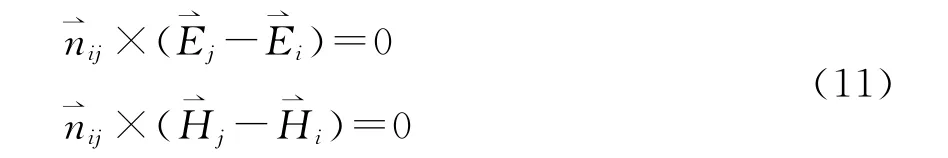
故(8)式、(9)式和(11)式即為V 中疊加解滿足的初始條件、外邊界條件和子區(qū)域邊界條件。
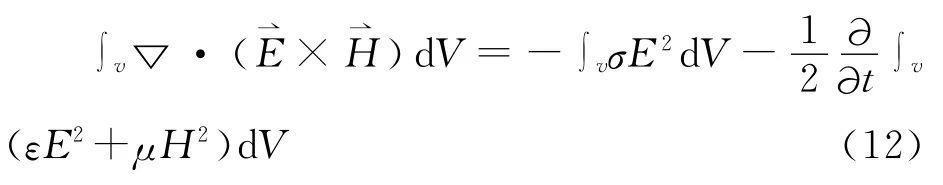
亦即
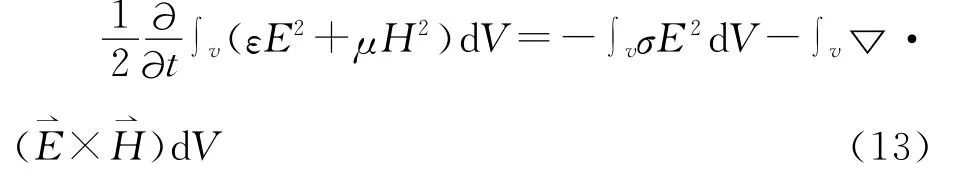
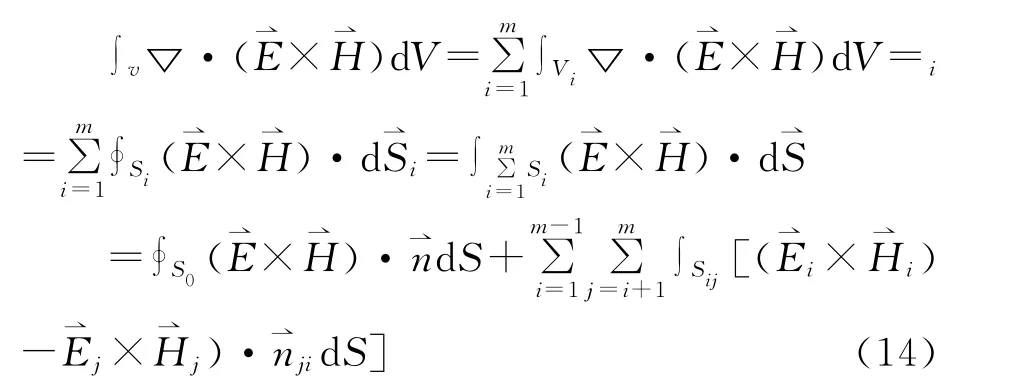
由(9)式


所以
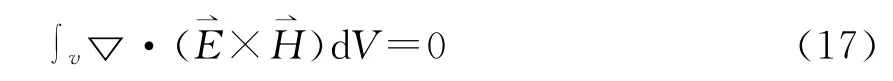
利用(17)式,對(13)式在t0至t>t0的時間積分得
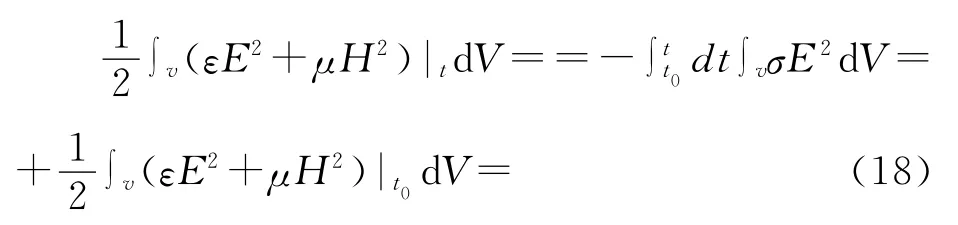
(18)式右邊的第1項,因為σ>0,E2>0故
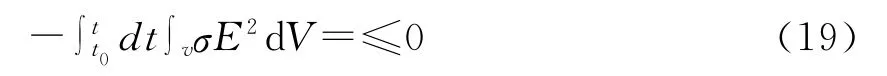
(18)式右邊的第2項,由(8)式
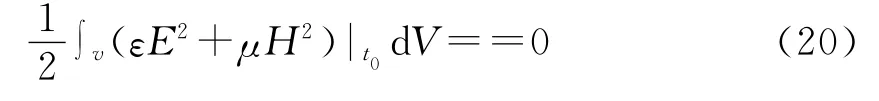
所以(18)式左邊有下式成立
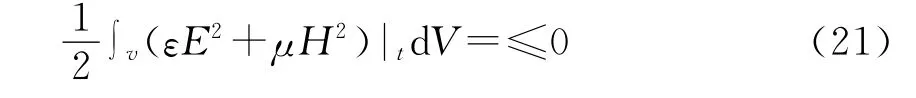
又(21)式左邊被積函數(shù)中每一項都大于或等于零,其積分必大于或等于零。那么(21)式成立的條件只可能是積分等于零,由此被積函數(shù)必等于零,于是
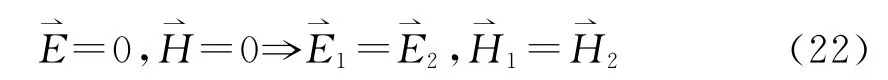
就是說,在給定初始條件和邊界條件的區(qū)域中,系統(tǒng)內的時變電磁場完全由麥克斯韋方程組惟一確定。
上述數(shù)學上的證明結果可以從物理上得到自然解釋。因為由子區(qū)域邊界條件和外邊界條件已經(jīng)證明∫v▽·()dV==0,因而(13)式可以寫為
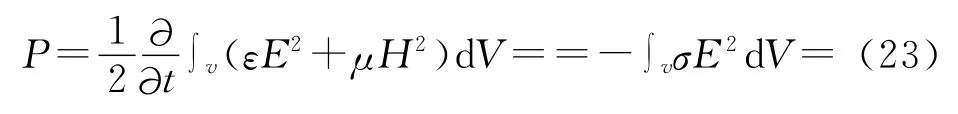
3 無限區(qū)域情形
如果所考慮的區(qū)域V是一個無限大區(qū)域,這可以認為在有限范圍內存在一個或幾個封閉的邊界面S′而不再有其它的邊界,如圖2所示。
對無限大區(qū)域,S′為有限范圍的邊界面,故S′上的邊界條件已知,并有前述(15)式的證明結果;對無限遠邊界,可任取某一定點為球心,作半徑為r的大球面Sr,先考慮包含在Sr和S′之內的區(qū)域Vr,再取r→∞的極限,此極限結果即可作為無限區(qū)域的結果。這時S0=S′+Sr,因而(14)式右邊的第1項變?yōu)?/p>
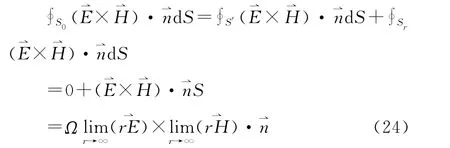
(24)式中Ω為無限大球面S對球心所張開的立體角。
若假定所有場源都位于有限區(qū)內,則電磁場在無限遠處滿足下列條件[11]
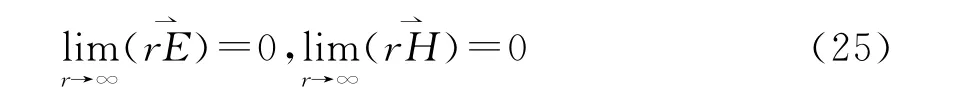
于是(24)式的面積分等于零。類似前述討論,同樣可以得到解的惟一性。
必須指出的是,對無限場域,當場點與場源間的距離充分大時,兩個場量的幅值均至少按距離反比減少;事實上,位于有限區(qū)域內的場源所產(chǎn)生的場在無限遠處均按1/r1+δ(δ≥0)的規(guī)律減少,因此條件(25)恒成立。
以上討論的是在σ≠0時得到結論。對σ=0的理想介質,因σE2=0,此時推不出E=0的結論。若規(guī)定在σ=0時的任何解都取σ≠0時的解在σ→0時的極限值,由于惟一解的極限只有一個,那么,用這種方式得到的解仍然是惟一的。
若單純從數(shù)學上求σ=0時麥克斯韋方程組的解,則解不惟一(可能有多個)。如空腔內的自由振蕩,不同幅度的振蕩都可以存在。然而,實際上任何物理介質都具有不同程度的損耗,把σ→0時的極限值作為小損耗介質是合理的。
4 時變電磁場惟一性定理的表述
綜上所述,時變電磁場的惟一性定理表述如下:
在均勻線性各向同性介質的空間區(qū)域中,給定t=t0時刻區(qū)域V 內各點電場和磁場的初始值,并同時給定t≥t0時子區(qū)域邊界條件
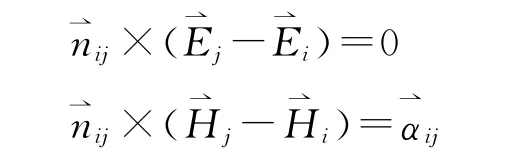
外邊界條件
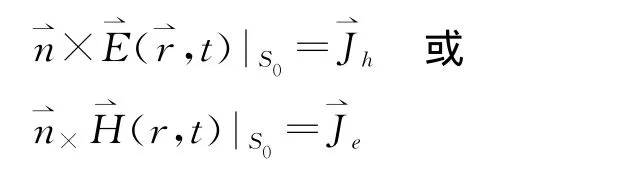
以及無限遠條件(只對無限區(qū)域情形)
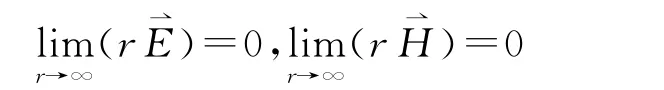
則區(qū)域V中的時變電磁場都有惟一解。
惟一性定理不僅指明可用任何方便的方法解電磁場,還可根據(jù)該定理建立解電磁場問題的等效原理,使原本不容易求解的電磁場變得比較容易求解。
5 討論
可見,時變電磁場的初邊值問題,只有在某些限定條件下(如線性介質、外邊界條件、無限遠條件等)應解麥克斯韋方程組以求時變電磁場的解才有可能存在惟一解。因為線性偏微分方程組的初邊值問題,在一般情形下并不存在惟一解。
介質的線性特性是時變電磁場初邊值問題存在惟一解的前提條件之一,對于非線性介質,一般不存在惟一解。如鐵磁質存在磁化曲線和磁滯回線;鐵電體存在電滯回線等。
應該指出的是:以上證明討論的是各向同性線性介質,因為方程組(1)、(2)式默認了介質的宏觀電磁性質方程成立的各向同性線性條件。對各向異性的線性介質,沿著上述類似的思路和方法,可以證明時變電磁場惟一性定理仍然成立。
[1]郭碩鴻.電動力學[M].2版.北京:高等教育出版社,1997.
[2]俞允強.電動力學簡明教程[M].北京:北京大學出版社,1999.
[3]Jackson J D.經(jīng)典電動力學:上冊[M].朱培豫,譯.北京:人民教育出版社,1978.
[4]董超鈾.惟一性定理的補充及證明[J].大學物理,1988(9):24-25.
[5]姚一民.惟一地確定矢量場的邊界條件[J].大學物理,1988(9):6-7.
[6]文盛樂.關于穩(wěn)定磁場惟一性定理的再討論[J].大學物理,1991(10):23-24.
[7]曹昌祺.電動力學[M].北京:人民教育出版社,1962.
[8]虞福春,鄭春開.電動力學[M].北京:北京大學出版社,1992.
[9]Stratton J A.Electromagnetic Theory[M].New York:McGraw-Hill,1941.
[10]Harrington R F.Time-Harmonic Electromagnetic Fiel dS[M].New York:McGraw-Hill,1961.
[11]方能航.電磁理論導引[M].北京:科學出版社,1986:137-168.

