小型無人直升機建模與魯棒控制研究

吳文海, 許麗, 王奇

(海軍航空工程大學 青島分院 三系, 山東 青島 266041)

小型無人直升機建模與魯棒控制研究

吳文海, 許麗, 王奇

(海軍航空工程大學 青島分院 三系, 山東 青島 266041)

以小型無人直升機為對象,采用分體法建立了完整的非線性飛行動力學數學模型。根據所建模型,進行了平飛狀態下的配平計算。根據配平結果,獲得了懸停時的線性狀態空間模型。在考慮風擾動的前提下,采用H∞靜態輸出反饋控制方法對無人直升機內外回路控制器進行了設計。仿真結果表明,所建模型的配平結果與直升機特性基本相符,驗證了模型的有效性;H∞綜合控制方法較好地實現了擾動下無人直升機狀態的控制,表明該算法具有良好的魯棒性、解耦性及跟蹤特性。

無人直升機; 直升機建模; 配平計算;H∞控制

0 引言

無人直升機因其構造簡單、靈活性好,在軍民領域得到了廣泛的應用[1]。然而,由于其高階、強耦合性、開環不穩定及非線性等特點,對飛行控制系統提出了很高的要求。無人直升機六自由度非線性運動模型是進行控制器設計及仿真的基礎,一般建模方法有基理建模法、神經網絡法[2]和系統辨識法[3-4]等。由于通道間耦合嚴重以及精確建模難以描述實際對象,因此具有魯棒特性的飛行控制系統設計顯得尤為重要。

本文采用分體法建立了無人直升機非線性飛行動力學模型,包括旋翼、尾槳、機身、垂直安定面以及水平安定面等部件模型。基于所建模型,進行了懸停及平飛狀態下的配平計算,并由配平計算結果得到了相應的線性化模型。針對懸停狀態下的線性化模型,采用基于H∞靜態輸出反饋控制方法進行了內外回路控制器的設計,并進行了擾動下的仿真驗證。

1 非線性動力學模型

假設槳葉為剛性、主旋翼轉速恒定,并忽略空氣壓縮性及槳葉失速影響。在機體坐標系下,無人直升機動力學方程描述為:

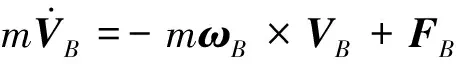
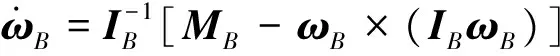
其中:

式中,FB為機體所受合外力在機體坐標系內的投影;IB為轉動慣量矩陣;MB為作用于機體質心的外力矩。

力和力矩為:

FB=Fmr+Fvf+Fhf+Ftr+FG

MB=Mmr+Mvf+Mhf+Mtr

式中,下標mr,vf,hf,tr分別表示主旋翼、垂直安定面、水平安定面、尾槳。

無人直升機相對于慣性坐標系的運動表達式為:

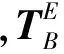
三軸姿態角運動方程為:

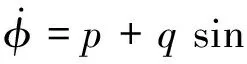
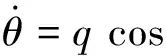
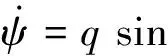
1.1 主旋翼及尾槳模型

主旋翼拉力為[6]:

式中,CTmr為拉力系數;Ωmr為旋翼旋轉角速度;Rmr為旋翼半徑。

拉力系數[7]表達式為:

式中,amr為槳葉升力線斜率;σmr為充填系數;λzmr為垂向速度引起的流入比;λ0mr為流入比;μmr為前進比;θ0mr為主旋翼總距角。

主旋翼揮舞動力學方程為:

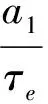
式中,τe為主旋翼揮舞運動的時間常數;a1,b1分別為槳尖軌跡平面相對于機體水平面的縱、橫傾角;λvmr為橫向速度引起的流入比;Aδlon,Bδlat分別為縱向周期變距和橫向周期變距與舵機輸入δlon,δlat的比值。

得到機體軸內的旋翼拉力為:

Xmr=-Tmra1

Ymr=Tmrb1

Zmr=-Tmr

主旋翼扭矩系數為:

式中,CD0mr為槳葉阻力系數。

忽略尾槳槳葉揮舞運動,除λztr和μtr與主旋翼不同外,其余相關參數相似,只需將公式中的下標mr改寫成tr。

尾槳產生的滾轉與偏航力矩為:

Ltr=Ttrhtr

Ntr=-Ttrltr

式中,htr,ltr分別為尾槳距機體質心的垂直高度及水平距離。

1.2 氣動部件模型

1.2.1 機身模型

機身三軸力可表達為:

Xfus=-0.5ρSxu2

Yfus=-0.5ρSyv2

Zfus=-0.5ρSz(w-Vimr)2

式中,Sx,Sy,Sz分別為機體x軸、y軸、z軸方向的有效氣動力面積;Vimr為主旋翼下洗流產生的誘導速度。由于機身結構具有對稱性,因此不考慮機身力矩影響。

1.2.2 水平安定面模型

考慮主旋翼下洗流影響,水平安定面垂向空速為:

whf=w-wwind+lhfq-KλVimr

式中,lhf為水平安定面至機體質心的水平距離;Kλ為主旋翼下洗流影響的權重系數。水平安定面產生的垂向力為:

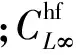
Mhf=Zhflhf

1.2.3 垂直安定面力與力矩

垂直安定面產生的側向力為:

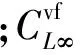
產生的滾轉與偏航力矩為:

Lvf=-Yvfhtr

Nvf=-Yvfltr

根據建立的非線性動力學模型,進行配平計算得到相應的平衡點。針對平衡點進行模型的線性化處理,具體方法見文獻[8],由此得到相應狀態下的線性模型,以便進行線性控制器設計。

2 H∞控制器設計

為提高無人直升機飛行控制系統的魯棒性,應用H∞綜合控制方法進行了內外回路的設計,控制系統結構圖如圖1所示。

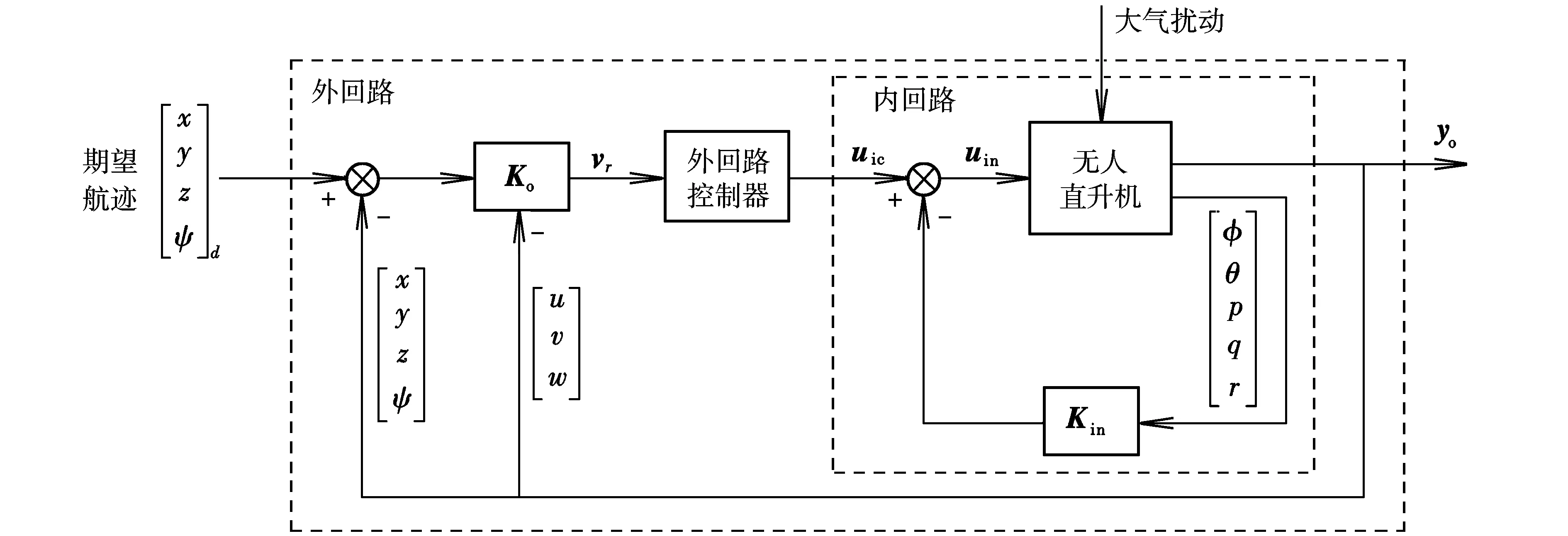
圖1 無人直升機H∞控制器結構圖Fig.1 H∞controller architecture of unmanned helicopter

2.1 求解反饋增益

采用最優控制算法求解靜態輸出反饋增益,該方法的優點在于不要求穩定的初始增益。反饋增益K的計算步驟如下:

(1)初始化。設n=0,L0=0,選擇增益γ、正定對稱矩陣Q和R。

(2)第n次迭代。由下式求出Pn:

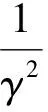
設置新的K與L值:

Kn+1=R-1(BTPn+Ln)CT(CCT)-1

Ln+1=RKn+1C-BTPn

(3)收斂性判斷。如果‖Kn+1-Kn‖<ε(ε=10-3),轉至步驟(4);否則,令n=n+1,回至步驟(2)。

(4)結束。置K=Kn+1。

2.2 內回路設計

通過選取H∞靜態輸出反饋增益Kin，實現跟蹤與通道間的解耦。為抑制紊流影響,線性模型中需要考慮氣流擾動項,通過矩陣Din輸入。懸停狀態下的線性模型為:

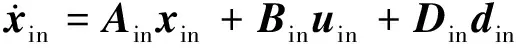
yin=Cinxin

式中,狀態xin=[u,v,p,q,φ,θ,a1,b1,w,r,rfb]T;控制輸入uin=[δlat,δlong,δcol,δped]T;輸出yin=[φ,θ,p,q,r]T;din為隨機風擾動。uin的表達式為:

uin=Kinyin+uic

式中,uic為內回路控制指令。

2.3 外回路設計

外回路采用單輸入、單輸出H∞回路成形法設計,設計方法見文獻[9]。

外回路控制器設計的目的是進行航跡指令的穩定與跟蹤,設計的對象模型為:

yo=Coxo

式中,狀態xo=[u,q,φ,θ,a1,b1,w,r,rfb,ψ,x,y,z]T;do為隨機風擾動;輸出yo=[x,y,z,u,v,w,ψ]T。

外回路輸出反饋控制律為:

uic=-Kovr

式中,vr=[(x-xr),(y-yr),(z-zr),u,v,w,(ψ-ψr)]T;(xr,yr,zr)為期望航跡指令。

3 仿真結果及分析

3.1 配平計算

以平飛速度V從0～24 m/s為配平條件,計算得到不同速度下的配平結果,如圖2和圖3所示。由圖2可以看出,旋翼總距和尾槳槳距隨著前飛速度的增加呈馬鞍型變化。由圖3可以看出,隨著前飛速度的增大,滾轉角變化不大,而俯仰角增加明顯。

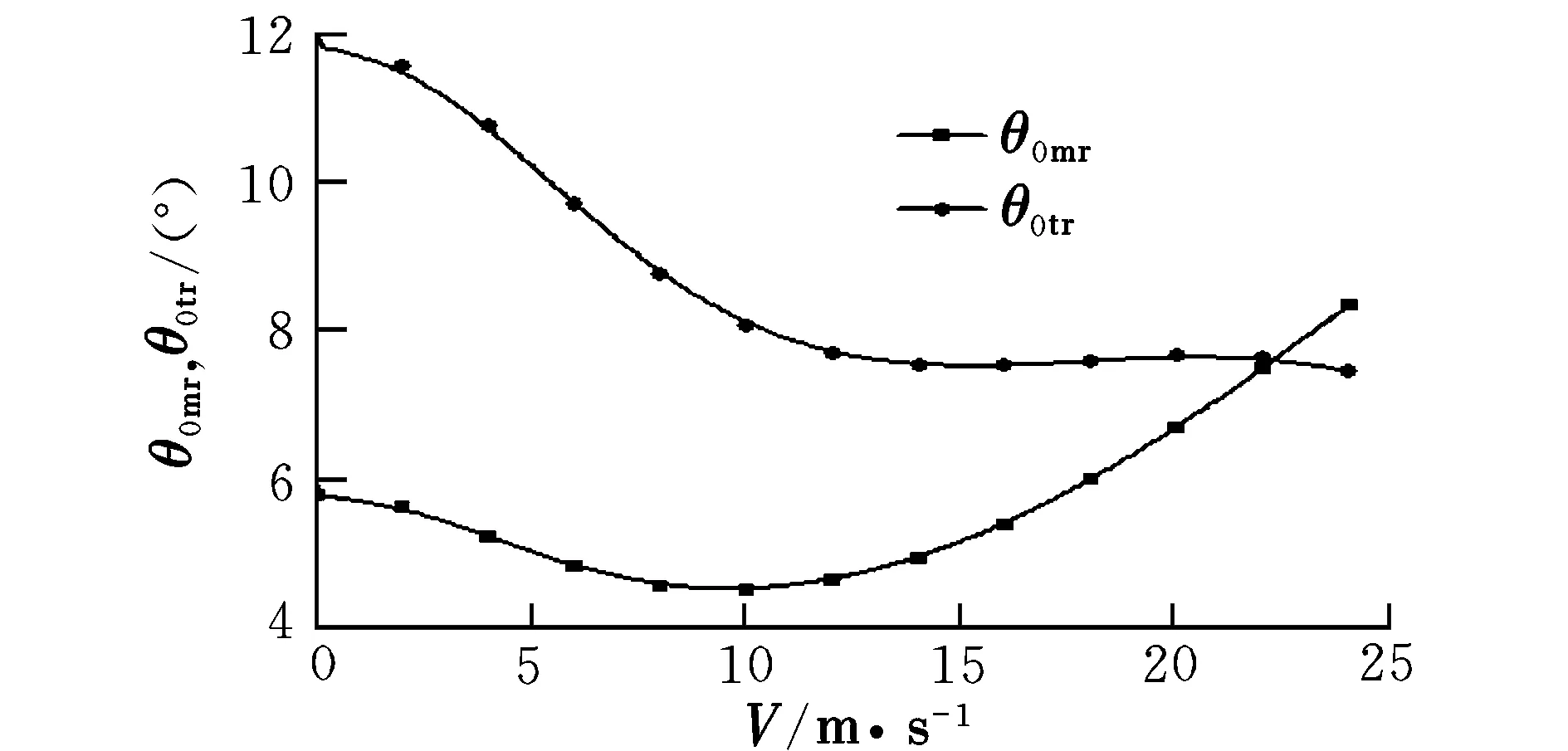
圖2 旋翼、尾槳總距隨前飛速度的變化Fig.2 Trimmed collective pitch of main rotor and tail rotor vs forward speed

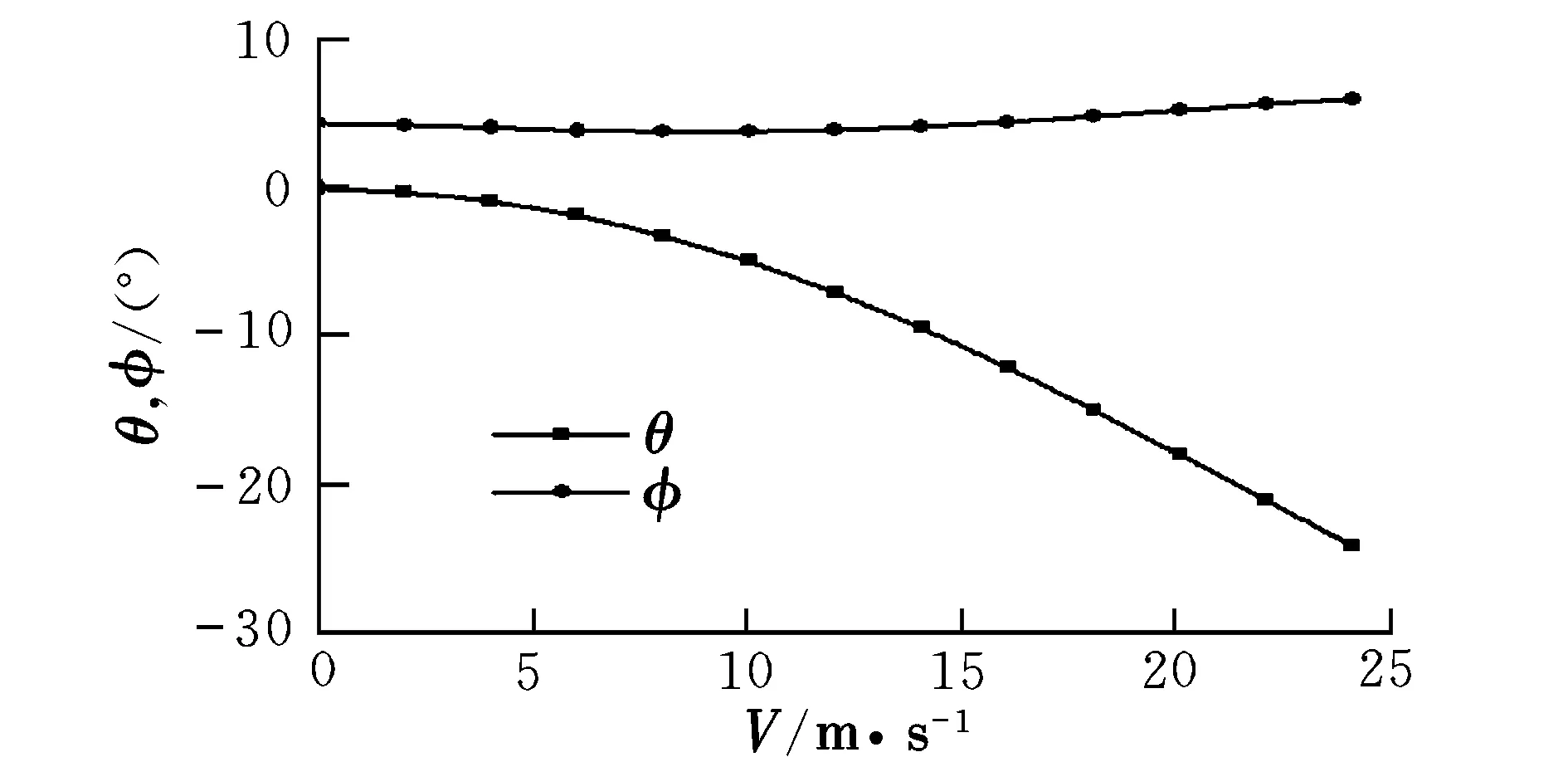
圖3 滾轉角、俯仰角隨前飛速度的變化Fig.3 Trimmed roll angle and pitch angle vs forward speed

3.2 飛行控制系統仿真

仿真結果如圖4～圖7所示。由圖4可知,在風擾動情況下,滾轉角和俯仰角收斂速度很快,保證了飛行的穩定性。由圖5可知,三軸角速度響應在3.5 s時已經達到穩定,有效地抑制了風擾動對角速度的影響。

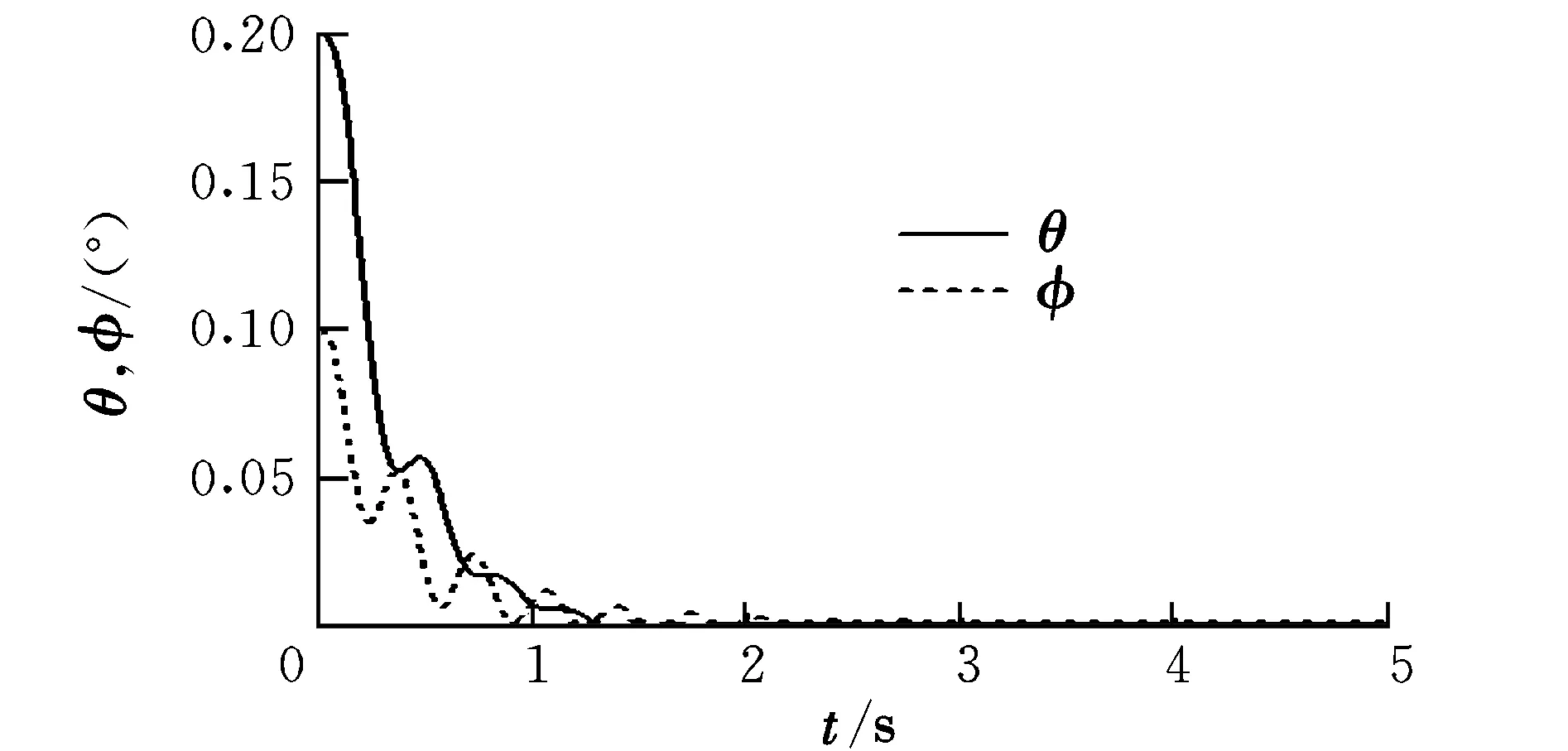
圖4 滾轉角和俯仰角響應Fig.4 Response of roll angle and pitch angle

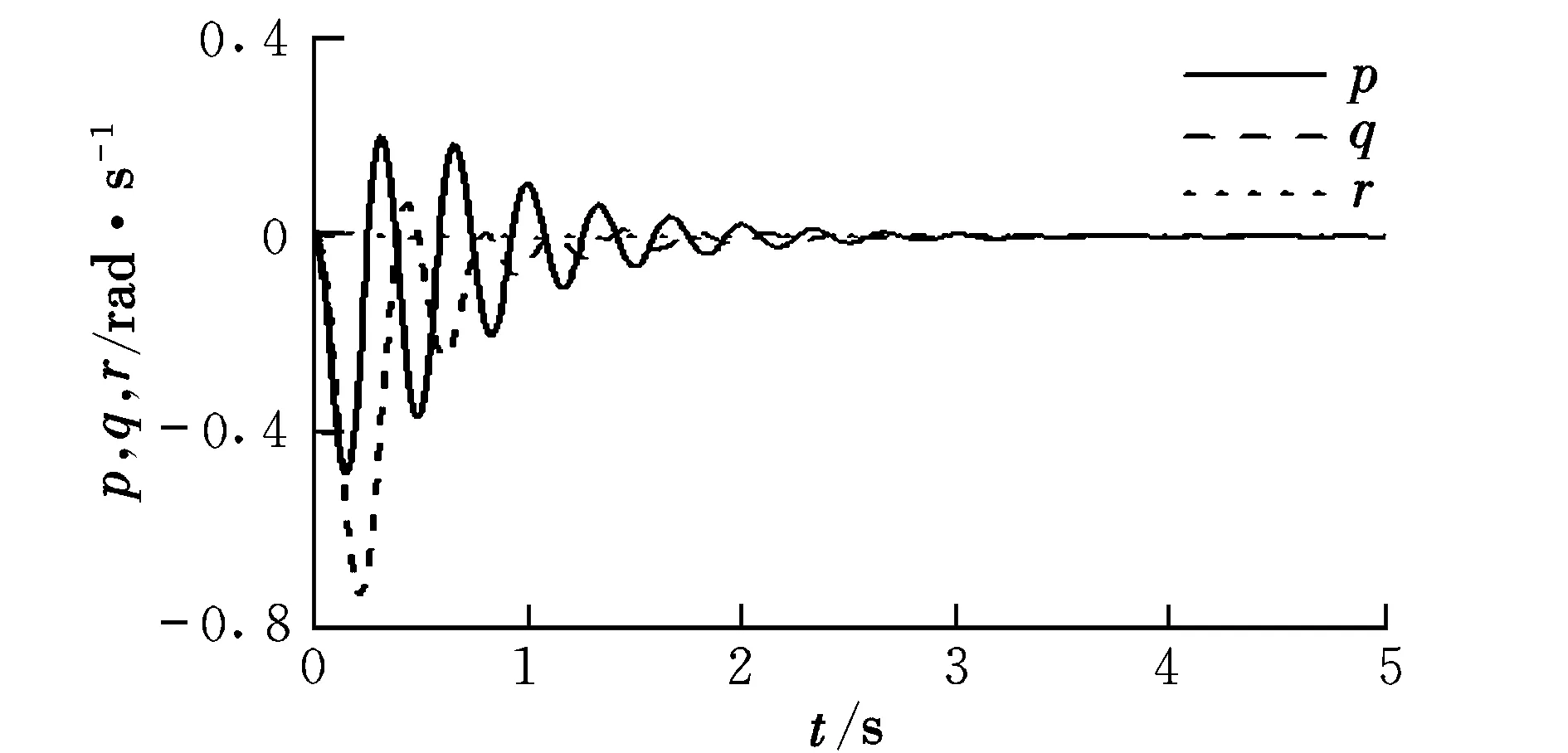
圖5 三軸角速度響應Fig.5 Angular velocity response

由圖6可知,位置響應在4 s左右恢復穩定值,實現了懸停狀態下的航跡保持。圖7為位置保持下的偏航角1°跟蹤響應。由圖7可知,響應無超調,上升時間小于1 s。

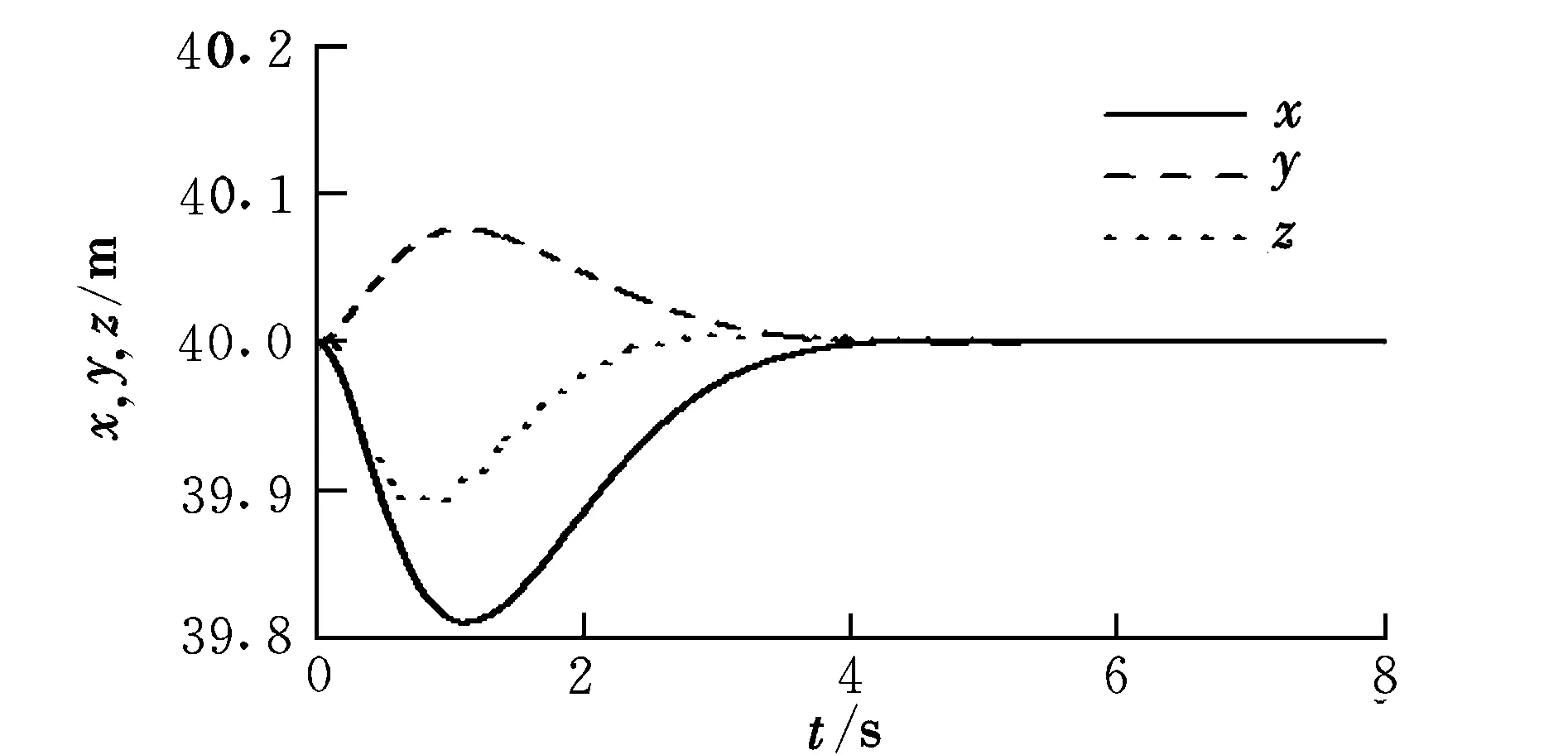
圖6 位置保持響應Fig.6 Position holding response

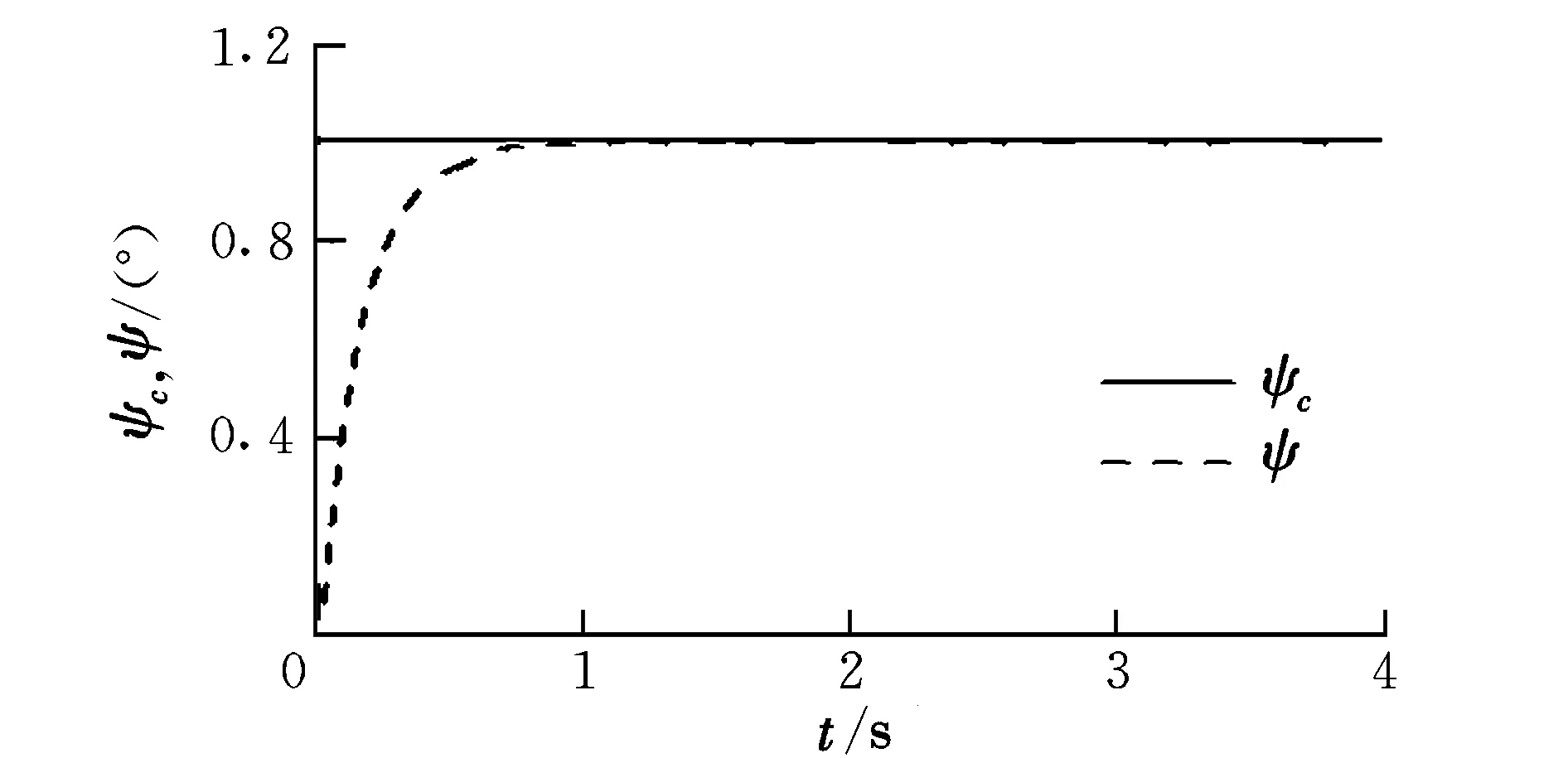
圖7 偏航角跟蹤響應Fig.7 Yaw angle tracking response

4 結論

通過本文研究可以得出以下結論:

(1)建立了小型無人直升機非線性飛行動力學模型,該模型適用于線性和非線性控制系統的設計與仿真。

(2)配平計算結果表明,所建模型符合直升機動力學特性,驗證了模型的有效性。

(3)采用H∞靜態輸出反饋控制方法設計了無人直升機內外回路飛行控制系統。結果表明,該控制算法具有較好的抗干擾及跟蹤性能。

[1] 吳文海,耿昌茂.直升機飛行控制系統[M].北京:海潮出版社,2001.

[2] Zein-Sabatto S,Zheng Y.Intelligent flight controllers for helicopter control [C]//In Proceedings of the International Conference on Neural Networks.Houston,1997:617-621.

[3] Hamel P G,Kaletka J.Advances in rotorcraft system identification[J].Progress in Aerospace Sciences,1997,33(3):259-284.

[4] Theodore C R,Tischler M B,Colbourne J D.Rapid frequency-domain modeling methods for unmanned aerial vehicle flight control applications [J].Journal of Aircraft,2004,41(4):735-743.

[5] Gordon L J.Principles of helicopter aerodynamics [M].USA:Cambridge University Press,2006:95-96.

[6] Gavrilets V.Autonomous aerobatic maneuvering of miniature helicopters[D].Boston:Massachusetts Institute of Technology,2003.

[7] Caglar Karasu. Small-size unmanned model helicopter guidance and control[D].Turkey:Middle East Technical University, 2004.

[8] 蔡國偉,陳本美.無人駕駛旋翼飛行器系統[M].北京:清華大學出版社,2012.

[9] Gary Balas,Richard Chiang,Andy Packard,et al.Robust control toolbox user’s guide[M].The Math Works,Inc.,2007:(2-11)-(2-20).

Researchonsmallunmannedhelicoptermodelingandrobustnesscontrol

WU Wen-hai, XU Li, WANG Qi

(The Third Department,Qingdao Branch, NAAU, Qingdao 266041, China)

Taking a small unmanned helicopter as the object, the full nonlinear equations of motion are developed with the multi-body method. Based on this model, the equations are trimmed under the level flight condition. According to the trimming results, the linear state space model in hover is achieved. Based on the hover model and considering the wind disturbance, inner and outer loop controllers are designed with the use ofH∞static output-feedback design method. Trim results show that the developed model is valid due to its consistency with the basic helicopter characteristics. Motion states of unmanned helicopter are well controlled byH∞synthesis method. Simulation results show that the control algorithm has good robustness, decoupling and tracking characteristics.

unmanned helicopter; helicopter modeling; trim calculation;H∞control

V249.1; V279

A

1002-0853(2013)06-0526-04

2013-03-07;

2013-09-06; < class="emphasis_bold">網絡出版時間

時間:2013-10-22 14:15

吳文海(1962-)，男，江蘇泰興人，教授，博士，主要研究方向為精確制導與飛行控制。

(編輯：姚妙慧)