高超聲速飛行器自適應BTT末制導律

2013-11-05 06:56:08李惠峰葛亞杰李昭瑩

北京航空航天大學學報 2013年5期

關鍵詞：指令

李惠峰葛亞杰李昭瑩

(北京航空航天大學宇航學院，北京100191)

高超聲速飛行器具有飛行速度高和突防能力強與殺傷威力大等特點，如果能夠達到直接命中的效果，就可以利用其動能毀傷目標.美國軍方提出高超聲速巡航導彈末制導的圓誤差概率(CEP，Circular Error Probable)小于3 m，而角度誤差小于0.5°，這就要求末制導律具有高精度的定向定點打擊能力.

為解決定向末制導問題，針對二維平面內的定向攔截，假設末段攻擊過程中飛行速度不變，且初始角度與要求的打擊角度偏差很小，基于改進的比例導引得到了解析的制導律［1］.基于導彈速度不變的假設設計了一種帶末端落角約束的變結構導引律［2］.但實際的末速度可能降到初速的40%以下，甚至更小，而初始角度也很難與所要求的打擊角度接近，因此基于末速度不變假設得到的制導律效果并不理想.

針對定向末制導問題，文獻［3］基于線性化系統，將問題簡化為具有終端角度約束的平面攔截問題，采用純數值優化方法得到制導軌跡.這種完全依靠數值計算的尋優方法缺乏工程上要求的實時性和可靠性，當擴展到三維空間時，可能不收斂或收斂很慢.文獻［4］設計了以控制能量最小為性能指標的最優導引律，在對剩余時間估算時考慮了飛行器速度大小與方向的變化，但剩余時間不可能精確地估計，產生偏差在所難免，這種偏差對于打擊精度有直接影響，特別是末制導階段，剩余時間較短，偏差所占比例較大.

文獻［5］對橫向比例導引律的收斂性進行了分析和證明.文獻［6］對HL-20的末段打擊提出了一種新的比例導引律，根據當前和最終狀態來調整比例因子，從而實現對非機動目標的定向打擊.文獻［7］在文獻［6］的基礎上針對高超聲速飛行器提出了一種自適應比例導引方法，不同于其他制導方法，此方法不依靠速度常量或線性化近似，在飛行器的機動性能范圍內，此制導方法能引導飛行器在任何初始條件下飛向目標.從其仿真結果中可以看出真正進入縱向調整的時間很短，比例因子的自適應效果不是很理想，容易導致打擊失敗.

本文針對高超聲速飛行器末端定向定點打擊，在文獻［6］的基礎上提出了一種具有自適應能力的高精度比例導引律.為確保飛行器有足夠的時間進行橫縱向調整，設計了一種合理的收斂策略，大大提高了比例導引進入的時間，保證落角落點約束的滿足.由于比例導引只考慮了運動學關系，而實際應用中需要考慮飛行器動力學約束，飛行器有可能無法理想地響應給出的制導指令，從而出現制導誤差，因此針對制導參數設計了閉環非線性自適應律，保證了高精度打擊效果.

1 末制導問題建模

1.1 末制導坐標系

在定向末制導問題中，由于彈目之間的距離較近，飛行器速度較大，因此可以忽略地球曲率和自轉，定義與目標固連的末段坐標系如圖1所示.

目標固連在原點O，x軸指向東，y軸指向北，z軸垂直向上，組成右手直角坐標系.其中，θ為視線偏角，φ為視線傾角，正方向如圖1所示.

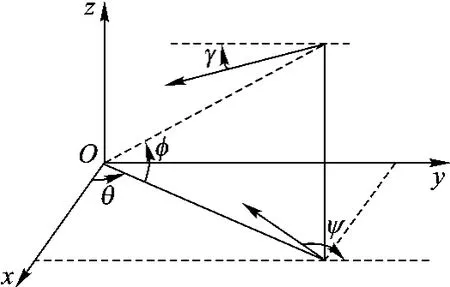
圖1 末制導坐標系

1.2 動力學模型

根據以上假設得到簡化動力學方程如下:

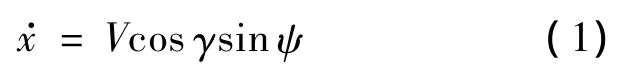
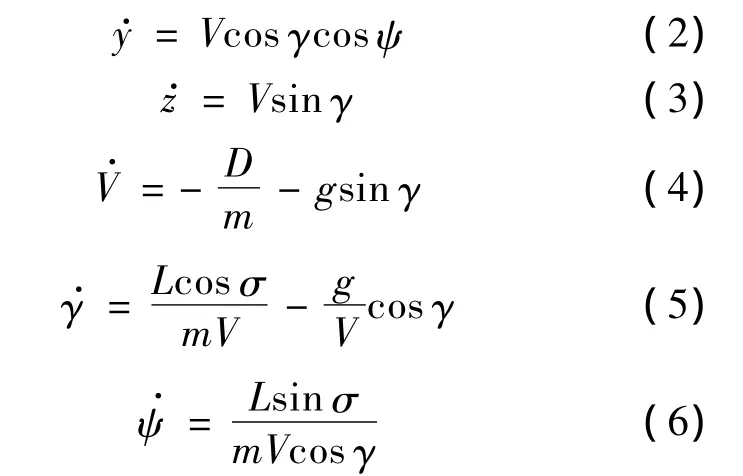
式中，x，y，z描述彈目相對位置;V為彈目相對速度;ψ為速度偏角;γ為速度傾角;重力加速度g=9.81 m/s2;m為常數;升力L和阻力D與高度z、速度V和攻角α有關:

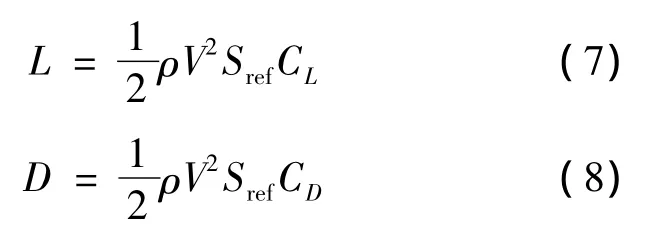
式中，ρ為大氣密度;Sref為參考面積;升阻力系數CL和CD是馬赫數和攻角的函數.

1.3 末制導約束

固定目標位于原點，定向打擊任務要求高速飛行器以規定角度命中原點，即軌跡終端約束為

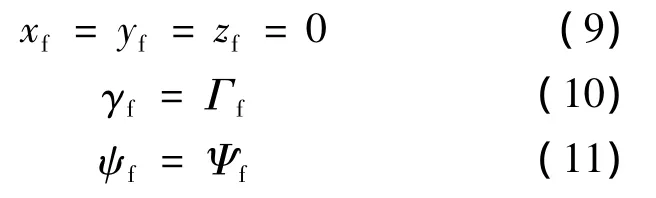
式中，zf為終端高度;Γf和Ψf是給定的命中目標時的速度傾角和偏角.

2 末制導策略

盡管有很多制導方法可以實現定點打擊，但只有少數能夠方便地實現對速度傾角和偏角的約束，本文采用比例導引法來實現定向末制導:

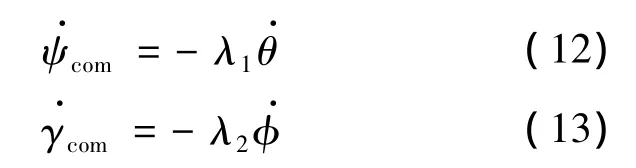
通過恰當地選擇制導參數λ1和λ2可以實現末制導約束.對于制導參數的選擇可以通過對文獻［6］的分析得到如下結論:

1)在任意速度下，當滿足|γ|＜90°，且對于任意的初始條件 θ(0)+ψ(0)≠π/2，λ1＞1，可以保證剩余距離趨于0.

2)當λ1＞2時，且滿足 θ+ψ=-π/2，軌跡在水平面上的投影將收斂到一條通過原點的直線.

3)在任意速度下，當 λ1＞1，λ2＞1時，可以保證趨于0.

4)當 λ1＞2，λ2＞2，且滿足 θ+ψ=-π/2和φ+γ=0時，飛行器在三維空間的軌跡將收斂到一條通過原點的直線.

本文采取的末制導策略是:橫向制導律先保證飛行器的航向對準目標，之后縱向制導律開始工作，使得速度傾角接近預期的值并導引飛行器飛向目標，同時橫向制導律能夠保證正確的航向.

2.1 橫向制導律

假設 ψ·= ψ·com，對式(12)在［t0，t］上進行積分:

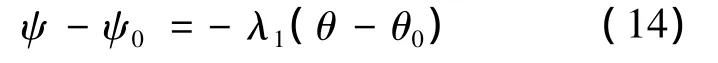
其中，ψ0和θ0是t0時刻的值，t0時刻即為橫向制導律進入工作狀態的瞬間.當λ1＞2時，為滿足末制導對于橫向的約束，飛行器的速度偏角漸近趨于穩定狀態Ψf，由θ+ψ=-π/2可以推出θ對應的穩定狀態值應滿足:

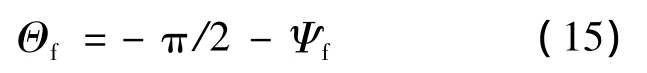
在式(14)中將ψ替換為Ψf，θ替換為Θf，可推出獨立變量λ1的取值應滿足如下關系:

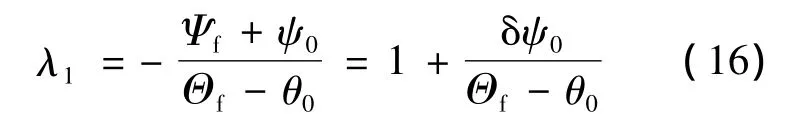
其中，δψ0是飛行器初始航向偏移量，滿足δψ0=ψ0-(-π/2-θ0).從前面的討論可知，如果 λ1＞2，那么此時λ1的值可以保證橫向約束實現.由式(16)計算出的λ1值在t0時刻要小于2，利用飛行過程中的當前值θ和δψ分別替代θ0和δψ0在λ1＞2之前導引飛行器飛向目標.

下面介紹橫向制導邏輯如何完成航向對準.如果Γf=-90°則在整個飛行過程中，任意一個大于2的常數λ1都能保證橫向對準;如果Γf≠-90°，且由式(13)計算得出的初始 λ1＜2，飛行器的傾斜角滿足如下關系:

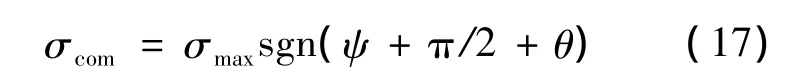
其中，σmax∈(0，90)是轉彎所需的最大傾斜角.當此制導指令發出之后，δψ0和θ0被其當前值所替代，從而可以通過式(16)計算出λ1的值.如果此時λ1＞2，那么當前時刻被設定為t0，將λ1的值代入式(10)來導引之后的末段飛行.

2.2 縱向制導律

上述結論也適用于式(13).假設飛行器理想的響應制導指令，對 γ·com=- λ2φ·積分得

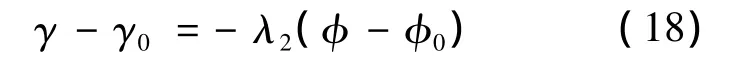
其中，γ0和φ0對應初始時刻的值.當λ2＞2時，為滿足末制導對于橫向的約束，飛行器的速度傾角漸近趨于穩定狀態Γf，可以推出:

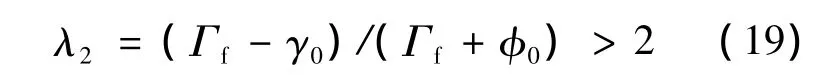
保證終端條件γf=Γf的實現需要選擇合適的比例因子，而比例因子的選擇在落角控制中存在兩個明顯的問題:

1)上述推導基于理想飛行器動力學假設，在實際俯沖段飛行過程中，由于飛行器機動能力有限，不能保證制導指令被理想響應，這將直接導致終端條件γf=Γf出現誤差.為解決該問題，在第3節將對比例因子引入自適應機制.

2)俯沖平面內軌跡對應的實際比例因子只有滿足λ2＞2，才能保證終端條件γf=Γf成立，需要設計相應的進入策略，保證在合適的時間滿足該條件，使得軌跡最終滿足落角約束.

由式(19)可以推出:

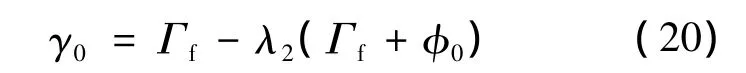
將式(20)中的 γ0替換為 γ，φ0替換為 φ，與tanφ=z/s聯立可得s與γ的關系:

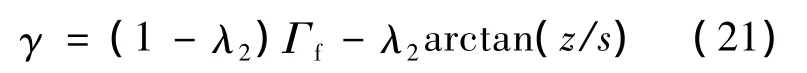
在俯沖平面內給出滿足條件所需的最小速度傾角，如圖2與圖3所示，可以看出:在相同距離下，隨著飛行高度的下降，速度傾角下限增加;隨著比例因子的增加，速度傾角下限增加;對應同一高度或者同一比例因子，隨著剩余距離的增加，速度傾角下限增加.

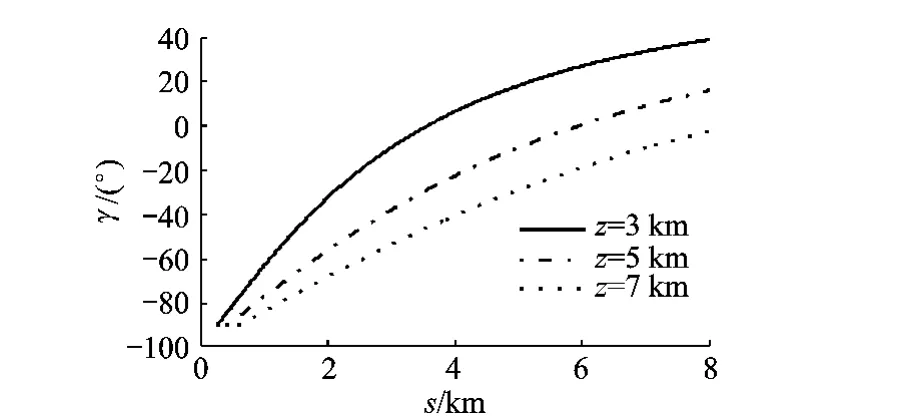
圖2 γ與s的關系(高度)

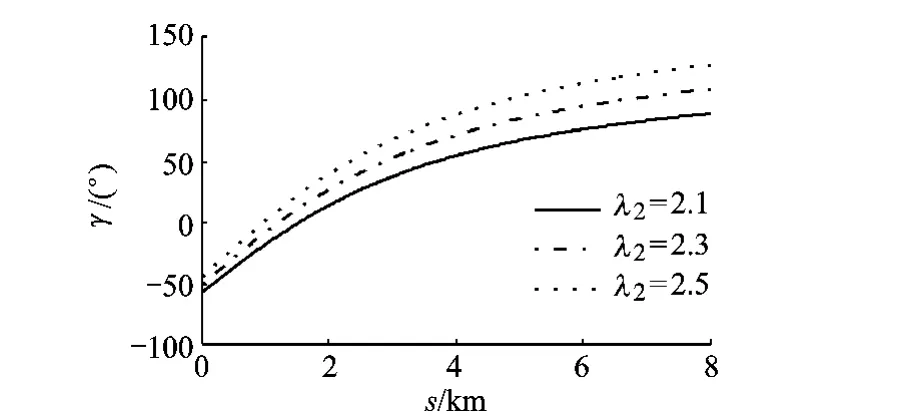
圖3 γ與s的關系(比例因子)

根據對滿足條件的最小速度傾角變化規律的分析，得到影響進入條件是否滿足的兩個主要因素:俯沖段初始速度傾角與進入策略.結合彈目視線俯仰角變化規律，給出進入飛行策略:速度傾角變化率與視線傾角變化率比值在1～2之間.

在飛行器進入末段之前，需要根據飛行器當前的狀態選擇合適的比例因子，從而在合理的時刻進入縱向比例導引的收斂段.進入條件滿足之后，縱向制導邏輯就開始工作，進入條件為其中，ε＞0是無窮小量.對于垂直打擊δψ應滿足:縱向制導邏輯控制過程如下:

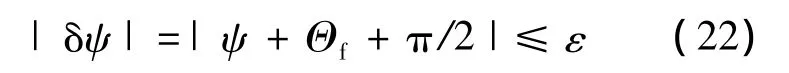
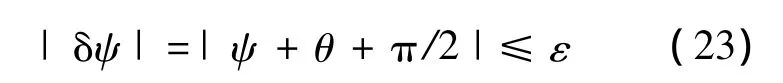
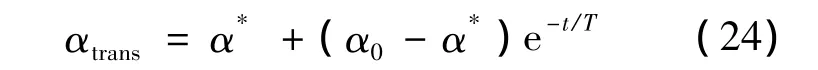
1)從末制導段初始時刻到航向對準結束，飛行器的攻角滿足如下關系:其中，α0為初始時刻的攻角;α*為飛行器最大升阻比所對應的攻角;時間常數T＞0是一個預設參數，來確保α0到α*可以快速、合理的轉換.

2)從航向對準段結束到λ2＞2時刻，縱向制導律中的導引參數為λ2＜1，λ2的值一旦大于2，此值將代入縱向制導律，由此開始縱向調整段.

3 自適應律

λ1和λ2這兩個參數一般確定后就保持某一常值不變.但在進入橫向和縱向控制階段后，會由于干擾等問題導致控制參數的實際值與指令值偏差較大，因此，之前確定的λ1和λ2的值不能再保證打擊角度的精度要求.

由式(6)和式(12)可以推出λ1的實際值:

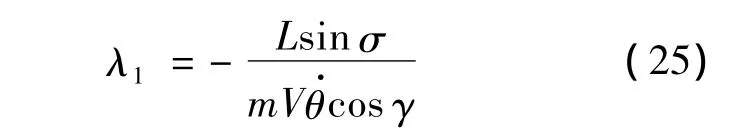
由式(5)和式(13)可以推出λ2的實際值:

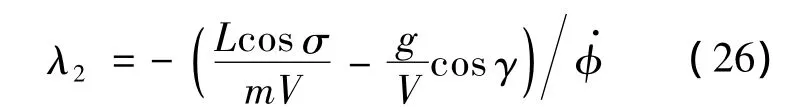
由于實際值和指令值存在偏差，需要實時計算其偏差是否在允許范圍內，如在允許范圍內，則保持當前值不變，如超出范圍，就需要重新計算并更新指令.在當前方法的框架內，利用這種閉環自適應實時更新λ1和λ2，能夠大大提高制導精度.比例因子的自適應機制流程圖如圖4所示.

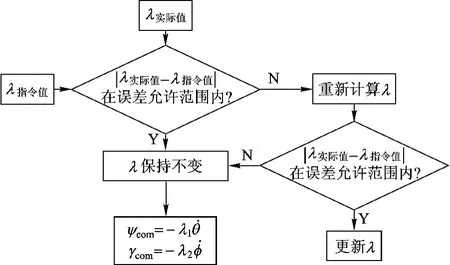
圖4 制導參數自適應控制流程圖

此外，由于輸出的制導指令是速度傾角與速度偏角的角速率指令，飛行器無法直接執行，因此需要轉化為攻角與傾斜角指令.

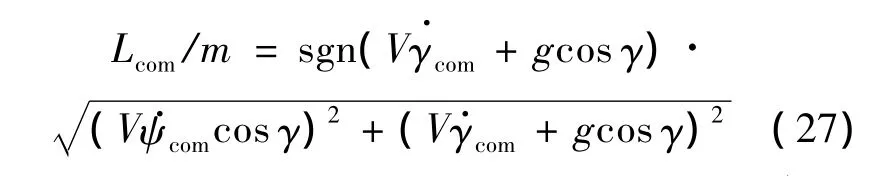
根據式(7)可以推出升力系數，利用飛行器的空氣動力學模型可以迭代求出當前馬赫數下的攻角指令αcom.把Lcom代入到式(6)可以得出傾斜角指令 σcom=arcsin(mV ψ·comcosγ/Lcom).

1)如果Kψ≥1，說明轉彎平面的角速率指令可以得到執行，傾斜角指令為

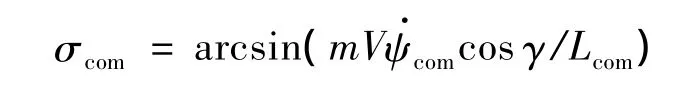
2)如果Kψ＜1，說明轉彎平面的角速率指令不能得到執行，傾斜角指令為

從式(5)和式(6)可推出當前的實際升力為

4 仿真結果

仿真所采用的飛行器模型來自文獻［8］.在如表1所示初始和終端條件下進行仿真，要求CEP＜3m，而角度誤差＜0.5°.

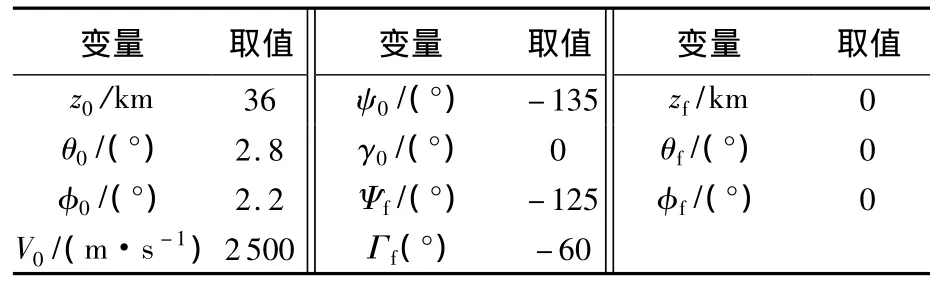
表1仿真條件

從圖5和圖6可看出導引律實現了飛行器對制導指令的準確跟蹤，最終打擊角度為 Ψf=-125°和Γf=-59.8°，打擊誤差在允許范圍內，實現了精確打擊，驗證了導引律的可靠性.

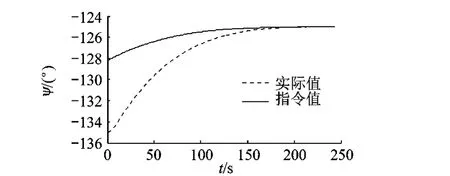
圖5 橫向制導律

從圖7和圖8可以看出制導參數實現了閉環自適應調節，在橫向制導階段λ1幾乎始終與所給指令保持一致，在進入縱向調整階段之后λ2也實現了對指令的準確跟蹤，保證了飛行器以特定的打擊角度攻擊目標，同時也保證了打擊精度.

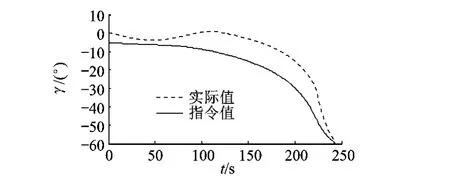
圖6 縱向制導律

圖7 制導參數λ1的變化

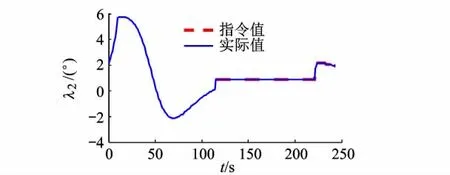
圖8 制導參數λ2的變化

從圖9中可以看出:飛行器在橫向制導律的作用下采取較大傾斜角，升力用于水平機動，先完成了傾斜轉彎，將速度偏角收斂到終端約束的較小范圍內;然后控制力轉向垂直平面內，在縱向制導律作用下下壓彈道，達到終端速度傾角，同時繼續微調速度偏角，直至命中目標.

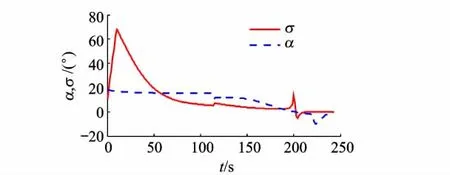
圖9 攻角和傾斜角的變化

圖10為飛行器的三維打擊效果圖，飛行器整個動態變化過程直觀地驗證了導引律的可行性.

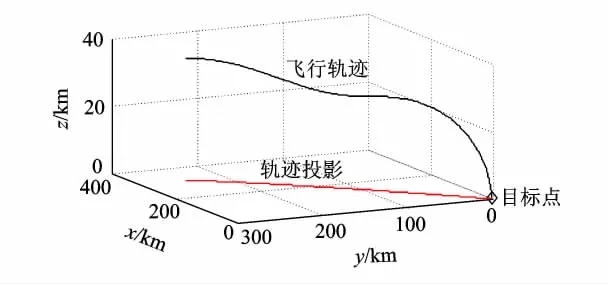
圖10 三維空間軌跡

5 結論

本文提出了一種高超聲速飛行器末段自適應制導律，能夠進行高精度的定點定向打擊，該方法具有以下特點:

1)進入比例導引的時間早，飛行器有足夠的時間進行橫縱向調整，保證了制導律的收斂性，使得落角落點約束能夠滿足;

2)考慮了飛行器的動力學約束，制導參數能夠自適應調整，減小了制導誤差，具有高精度的落點和落角，能夠準確命中目標.

仿真結果表明本文所提出的自適應末制導方法，實現了高精度的定點定向打擊，具有較好的工程實用價值.

References)

［1］ Kim B S，Lee J G，Han H S.Biased PNG law for impact with angular constraint［J］.IEEE Transactions on Aerospace and Electronic Systems，1998，34(1):277-288

［2］宋建梅，張天橋.帶末端落角約束的變結構導引律［J］.彈道學報，2001，13(1):16-20 Song Jianmei，Zhang Tianqiao.The passive homing missile’s variable structure proportional navigation with terminal impact angular constraint［J］.Journal of Ballistics，2001，13(1):16-20(in Chinese)

［3］ Song T L，Shin S J，Cho H.Impact angle control for planar engagement［J］.IEEE Transactions on Aerospace and Electronic Systems，1999，35(4):1439-1444

［4］朱戰霞，王建培.一種攻擊地面固定目標的變系數比例導引律［J］.飛行力學，2000，18(4):46-49 Zhu Zhanxia，Wang Jianpei.A gain variable proportional guidance law for stationary target［J］.Flight Dynamics，2000，18(4):46-49(in Chinese)

［5］ Lu P.Intercept of nonmoving targets at arbitrary time-varying velocity［J］.Journal of Guidance，Control，and Dynamics，1998，21(1):176-178

［6］ Ulybyshev Y.Terminal guidance law based on proportional navigation［J］.Journal of Guidance，Control，and Dynamics，2005，28(4):821-824

［7］ Lu P.Adaptive terminal guidance for hypervelocity impact in specified direction ［J］.Journal of Guidance，Control，and Dynamics，2006，29(2):269-278

［8］ Undurti A.Optimal trajectories for maneuvering reentry vehicles［D］.Massachusetts Avenue，Cambridge，MA:Massachusetts Institute of Technology，2007