基于光譜特征的自適應子空間波段選擇方法

徐 秋 李 娜 趙慧潔 李旭東

(北京航空航天大學精密光機電一體化技術教育部重點實驗室，北京100191)

較多光譜而言，高光譜數據能捕捉到地物在光譜特性上更細微的差異，并以足夠高的光譜分辨率來表達不同地物所具有的診斷性光譜特征.通過分析這些特征，能夠反演出地物構造的物理指標和內部化學組分的含量等［1］，因此高光譜數據在地物的定量化分析方面較其他遙感數據具有較大的優勢.但高光譜數據具有極強的波段相關性，圖像間存在大量冗余信息，降低了數據的應用效率，甚至包括地物分類或識別的精度.因此，有效利用高光譜數據的前提，是選擇合適的特征對高光譜數據進行降維處理.

波段選擇作為高光譜降維的重要手段一直是研究的熱點方向.現有波段選擇方法一般分為［2-6］:①基于信息量的波段選擇方法，如波段指數、自適應波段選擇;②基于類間可分性的波段選擇方法;③基于子空間劃分的波段選擇方法，即先對數據整體空間進行子空間劃分，然后在每個子空間內依據信息量或類別可分性等進行選擇.

從方法思想和最終結果來看，基于子空間劃分的波段選擇方法充分考慮了數據全局特性與局部特性的差異，最佳波段組合不僅合理分布且更能反映數據的局部特性，較其他兩類方法在理論上更具優勢.但現有的子空間劃分方法要么主觀判斷，子空間劃分較為呆板;要么統計波段中全體地物的信息，在局部細節體現上并未將感興趣地物與背景地物分開，子空間劃分容易受背景地物影響，提取的特征空間針對性不強，無法滿足數據定量分析與精細化應用的較高要求.

針對這一問題，本文對現有方法進行深入分析，突破光譜特征提取技術，通過引入反映感興趣地物局部光譜特性的指標，建立子空間劃分模型.該方法減少了背景地物對子空間劃分的影響，實現了針對感興趣地物最佳波段的有效提取.

1 方法實現

本文方法從感興趣地物的光譜曲線出發，提取任意兩類地物反射率絕對值距離的最大值和最小值，并以其乘積構建光譜自適應因子(SAF，Spectral Adaptive Factor);將SAF與波段的光譜信息組成子空間劃分模型，以聚類實現子空間劃分;以J-M距離實現子空間波段優化，最終在整個數據空間獲得最佳波段組合.

1.1 光譜自適應因子

分析高光譜數據自身特點，在某一光譜范圍內，當所有地物反射率變化較小、光譜曲線較為平緩時，各波段的信息量、類間可分性等統計參數在該光譜范圍內趨于一致;如果在該光譜范圍內，光譜特征因地物構造的某些物理指標或內部某些化學組分含量發生劇烈變化時，相應波段的信息量或類間可分性等也會產生巨大變化，這說明利用各波段信息量或類間可分性來衡量地物光譜特征的細微變化是可行的.當在地物診斷性特征波段上光譜發生巨大變化時，地物類別可分性增大或減小都存在一定可能，因此將類別最大可分性和最小可分性兩個指標結合使用，既可較好地表征地物光譜特征變化對地物整體類別可分性的影響，又對最難分地物的差別進行保留，而僅用兩者中的任一指標表征都是不全面的.

基于以上分析，本文提出在N類感興趣地物的光譜曲線上，建立光譜自適應因子，其公式為其中，ρik為k波段上第i類地物的反射率;ρjk為k波段上第 j類地物的反射率，且 i，j∈N，i≠j.

Smax是同一中心波長上，任兩類地物光譜絕對值距離的最大值，Smax表現了感興趣地物的最大可分性，反映了感興趣地物光譜在波段上的總體情況，從側面也反映了波段攜帶感興趣地物信息量的大小.Smin是同一中心波長上，任兩類地物光譜絕對值距離的最小值，Smin表現了感興趣地物的最小可分性，Smin越大，感興趣地物之間的性質相差越遠，最難分地物的可分性越大;Smin越小，感興趣地物中有兩類地物的性質相近，最難分地物的可分性越小.

由SAF定義發現，其值越大，該波段包含感興趣地物的信息越多，類別可分性越強.

1.2 子空間劃分

子空間劃分主要依據本征維數對模型進行聚類，自動劃分子空間，即估計本征維數m，將m作為聚類的類別數C，將SAF與波段的光譜信息組成子空間劃分模型，利用聚類方法將模型分為C類，每一類即為一個子空間.

在高光譜數據處理中，PCA(Principal Componet Analysis)方法是應用最為廣泛的本征維數估計方法之一，主要利用數據協方差矩陣的特征值λ對本征維數進行估計.PCA方法對維數為p的高光譜數據估計本征維數m的原則主要有:①選擇λm≠0的最大維數;②累計貢獻率G(m)達到足夠大(一般在85%以上).G(m)公式為

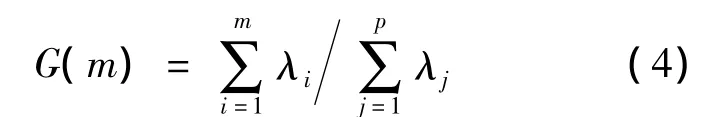
圖1是基于ENVI 4.4usgs_veg.sli地物數據庫中3類地物(草、金花矮灌木、干草)的子空間劃分，光譜范圍為0.4～2.5 μm，本征維數m為3.運用系統聚類方法將數據分為0.4～0.87 μm，0.87 ～1.66 μm，1.66 ～2.5 μm 3 個子空間.

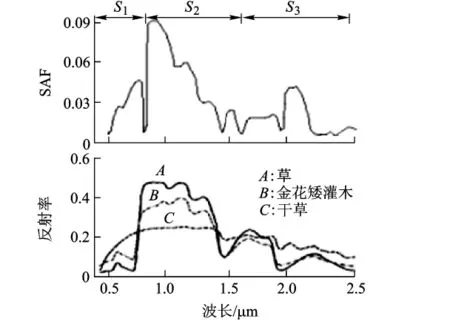
圖1 3類地物子空間劃分示意圖

1.3 子空間波段優化

高光譜遙感中，地物反射率受光照、成像光譜儀、遙感平臺、地物背景等各種因素影響，即使屬于同一種地物，在相同波長下各像元的光譜響應也略有差異.在進行波段選擇時，不能把子空間內SAF取值最大作為選擇最佳波段的唯一標準，還要考慮地物樣本的可分性.高光譜波段優化常用的類間可分性準則包括歸一化均值距離、離散度、J-M距離等［7］.歸一化均值距離的定義是均值之差的絕對值除以標準差之和，它只能運用在一維空間中，不能運用于多維空間.當類均值相等時，無論標準差如何變化，歸一化均值距離均為0，無法體現類別可分性的大小.

離散度、J-M距離都是基于類條件概率之差的.與歸一化均值距離僅考慮一階統計變量(平均值)相比，離散度、J-M距離進一步考慮了二階統計變量(協方差)給分類帶來的影響，克服了類均值相等給類別劃分帶來的不便.在離散度的定義中，歸一化距離起主要作用，而在J-M距離的定義中卻極大地降低了對一階統計變量的依賴;從類別距離與分類精度的關系考慮，離散度近乎指數上升，而J-M距離增加到一定程度就不再增加，收斂于某一數值，這與地物分類精度收斂于100%性質一致.J-M距離比離散度更能較好地體現類別距離與分類精度的實際關系，因此在算法中選用J-M距離作為子空間類間可分性準則，其公式為

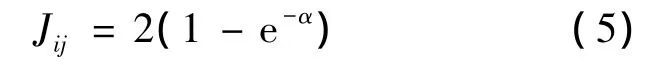
其中，α為巴氏(Bhattacharyya)距離.

在每個子空間內計算每個波段地物平均J-M距離，并從大到小排序，選擇距離最大的波段作為子空間的最佳波段;將子空間的最佳波段最終組合為整個空間的最佳波段組合.

2 試驗與結果分析

2.1 試驗結果

試驗數據由AOTF(Acousto-Optic Tunable Filter)成像光譜儀拍攝而成，包含A，B，C 3類地物(圖2)，波譜范圍571～902 nm.其中171～180波段(757～775 nm)受氧氣吸收影響反射率偏低，不予采用.最終待選波段為1～170波段(571～757 nm)和181～244波段(775～902 nm)共234個波段.基于PCA變換后特征值排列情況，研究區的本征維數m為3.

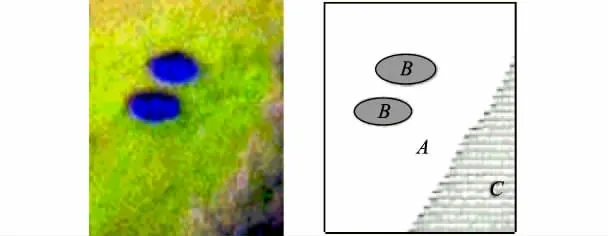
圖2 研究區假彩色影像及空間關系示意圖

提取3類地物的光譜曲線(圖3)建立子空間劃分模型(圖4)，選擇系統聚類法劃分子空間.對n個樣本，系統聚類的基本思想是規定樣品之間的距離和類與類之間的距離，在聚類開始時將n個樣本各自作為一類，然后將距離最近的兩類合并成一個新類，計算新類與其他類之間的距離，重復進行最近類的合并，直到最后所有樣本合并為一類并形成一個聚類樹形圖，從圖上能看出應分為幾類及每類包含的樣本.在系統聚類中，選擇Euclidean距離、質心距離分別表示樣本之間和類與類之間的距離，聚類后234個波段分為3組:1～145波段、146～215(除去171～180)波段及216～244波段.在3組波段中，依據3類地物平均J-M距離選擇720 nm，800 nm，894 nm 3波段為最佳波段組合.

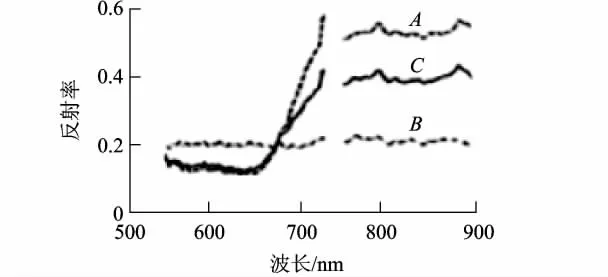
圖3 3類地物光譜曲線

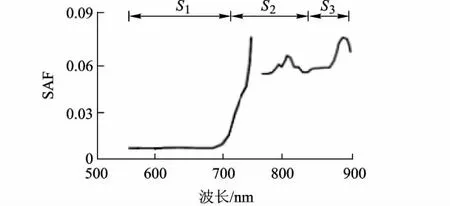
圖4 3類地物的子空間劃分

為驗證方法性能，選擇基于類間可分性最佳波段選擇和波段指數(BI，Band Index)兩種方法，對最佳波段組合進行對比，3種方法波段選擇的最終結果如表1所示.

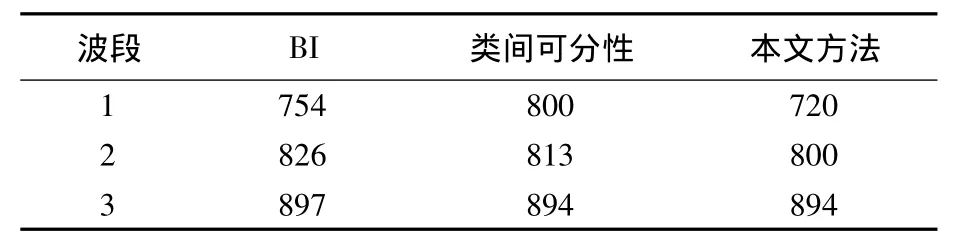
表1 3種方法的最佳波段組 nm

2.2 主觀評價

圖5為3組最佳波段組合的融合圖像.從視覺效果比較，在基于本文方法的融合圖像上，A，B，C 3類地物對比強烈，可分性最好.

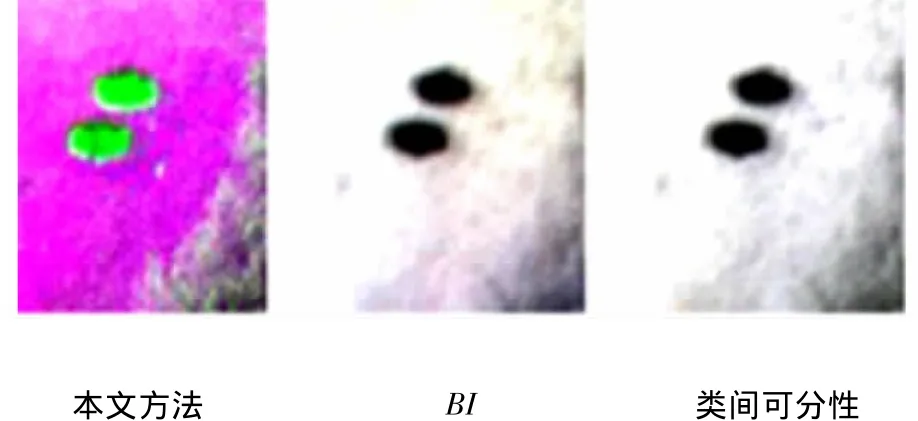
圖5 3組最佳波段組合融合圖像比較

2.3 客觀評價

為進一步定量對比，在圖像上隨機采樣，各地物樣本采樣個數如表2所示.以地物J-M距離為衡量標準，進行樣本可分性評價.Jij取值在(0，2)之間.Jij在(0，1)時，樣本間不具有光譜可分性;Jij在(1.0，1.9)時，樣本間具有一定的光譜可分性，但存在較大程度的重疊;Jij在(1.9，2.0)時，樣本間具有很好的光譜可分性［8］.

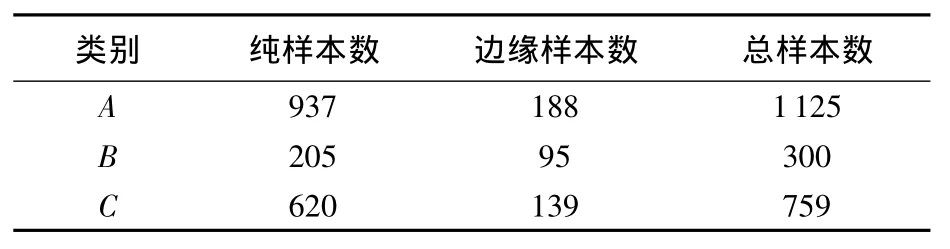
表2 3類地物樣本個數

表3分別列出在3組最佳波段組合中，任意兩類地物純樣本之間、邊緣樣本之間以及3類地物平均J-M距離的大小.試驗結果表明:3種方法純樣本之間的J-M距離都在1.9以上，樣本間具有光譜可分性;在邊緣樣本分類中，A和B，B和C的J-M距離在1.9以上，樣本間具有光譜可分性;但光譜相似的A，C兩類，3種方法邊緣樣本之間的J-M距離均小于0.5，表明樣本間不具有光譜可分性.從3類地物的平均J-M距離比較，本文方法3類地物的平均J-M距離略高于另外2種方法，樣本可分性最大，地物重疊程度最小.

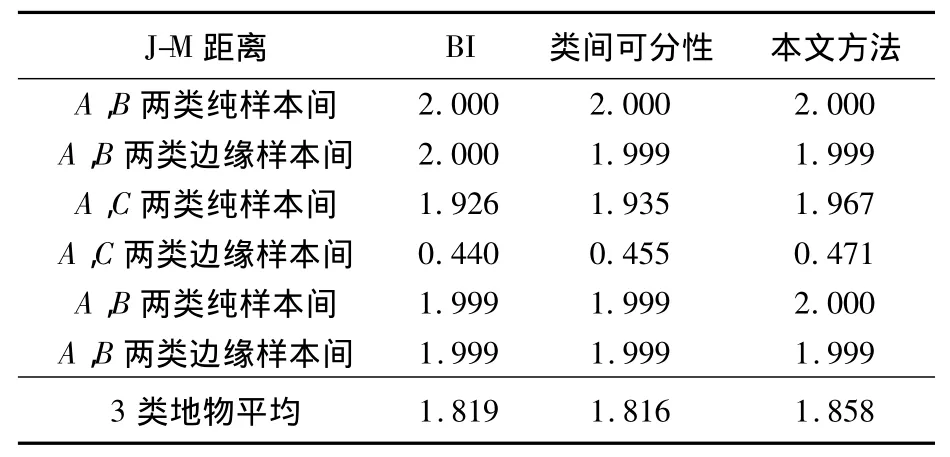
表3 3組最佳波段子集J-M距離

采用最大似然法［9］對 720 nm，800 nm，894 nm 3波段組合進行地物分類.最大似然法假定每個波段的每一類統計都呈均勻分布，計算像元屬于某一特定類別的似然度，每個像元被歸并到似然度最大的那一類中.地物分類的混淆矩陣見表4，地物分類結果見圖6.

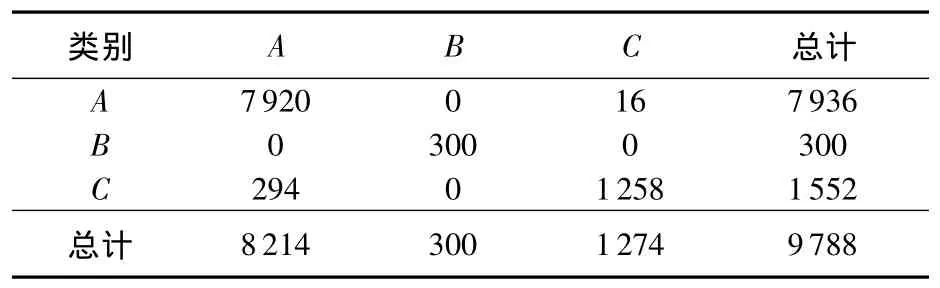
表4 3波段分類后的混淆矩陣

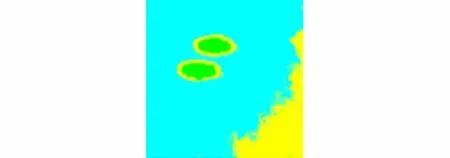
圖6 maximum likelihood分類圖

總體分類精度:

(7920+300+1258)/9788×100%=96.832%Kappa系數為0.894.

錯分原因:①分類精度受測試者主觀因素影響.訓練樣本隨機采樣，不同測試者會選取不同的樣本，樣本的分布情況會影響分類效果;②邊緣樣本間相互干擾，分類純度不高，導致精度降低.

3 結論

針對現有波段選擇方法存在問題，本文通過引入反映感興趣地物局部光譜特性的指標，建立子空間劃分模型，提出一種基于光譜特征的自適應子空間波段選擇方法.利用AOTF高光譜數據對方法性能進行分析與驗證，結果表明:本文方法具有較強的有效性和實用性.

References)

［1］童慶禧，張兵，鄭蘭芬.高光譜遙感——原理、技術與應用［M］.北京:高等教育出版社，2006:1-3 Tong Qingxi，Zhang Bing，Zheng Lanfen.Hyperspectral remote sensing:the principle，technology and application［M］.Beijing:Higher Education Press，2006:1-3(in Chinese)

［2］韓瑞梅，楊敏華.一種改進的高光譜遙感數據波段選擇方法的研究［J］.測繪與空間地理信息，2010，33(3):137-139 Han Ruimei，Yang Minhua.Study on an improved method of band selection of hyperspectral remote sensing data［J］.Geomatics ＆ Spatial Information Technology，2010，33(3):137-139(in Chinese)

［3］蘇紅軍，盛業華.基于正交投影散度的高光譜遙感波段選擇算法研究［J］.光譜學與光譜分析，2011，31(5):1309-1313 Su Hongjun，Sheng Yehua.Orthogonal projection divergence based hyperspectral band selection［J］.Spectroscopy and Spectral Analysis，2011，31(5):1309-1313(in Chinese)

［4］ Huang Rui，He Mingyi.Band selection based on feature weighting for classification of hyperspectral data［J］.IEEE Geoscience and Remote Sensing Letter，2005，2(2):156-159

［5］ Bajcsy P，Groves P.Methodology for hyperspectral band selection［J］.Photogrammetric Engineering and Remote Sensing Journal，2004，70(7):793-802

［6］劉春紅.超光譜遙感圖像降維及分類方法研究［D］.哈爾濱:哈爾濱工程大學信息與通信學院，2005 Liu Chunhong.Research on dimensional reduction and classification of hyperspectral remote sensing image［D］.Harbin:College of Signal and Information Processing，Harbin Engineering University，2005(in Chinese)

［7］張良培，張立福.高光譜遙感［M］.北京:測繪出版社，2011:83-87 Zhang Liangpei，Zhang Lifu.Hyperspectral remote sensing［M］.Beijing:Surveying and Mapping Press，2011:83-87(in Chinese)

［8］齊臘，劉良云，趙春江，等.基于遙感影像時間序列的冬小麥種植監測最佳時相選擇研究［J］.遙感技術與應用，2008，23(2):154-160 Qi La，Liu Liangyun，Zhao Chunjiang，et al.Selection of optimum periods for extracting winter wheat based on multi-temporal remote sensing images［J］.Remote Sensing Technology and Application，2008，23(2):154-160(in Chinese)

［9］孫麗娟.基于支持向量機的高光譜圖像分類技術研究［D］.哈爾濱:哈爾濱工程大學信息與通信學院，2011 Sun Lijuan.Research on classification of hyperspectral images based on support vector machine［D］.Harbin:College of Signal and Information Processing，Harbin Engineering University，2011(in Chinese)