月球著陸器著陸腿非線性有限元建模與仿真

梁東平 柴洪友 曾福明

(北京空間飛行器總體設計部，北京100094)

月球著陸器著陸緩沖分系統的主要功能是緩沖著陸器月面軟著陸時的沖擊載荷，保證結構和有效載荷不因著陸沖擊而破壞，并吸收著陸過程中的動能，使著陸器安全著陸到月面上.由于著陸沖擊試驗成本高、周期長、難度大，只能進行有限次數的特定工況地面模擬驗證試驗，因此必須開展大量著陸沖擊動力學仿真分析，驗證著陸緩沖分系統的性能，獲得相關性能參數，從而為著陸緩沖分系統的優化設計和試驗驗證提供指導，并為著陸器結構和儀器設備的設計提供輸入條件［1-4］.

著陸緩沖分系統著陸沖擊仿真大多數是基于多剛體動力學模型，多剛體模型比較簡單，計算效率高，但沒有考慮結構柔性［5-7］.為研究結構柔性對著陸腿性能的影響，通常采用部件模態綜合的方法.通過有限元分析軟件生成著陸腿的模態中性文件，并導入多體動力學軟件中，建立柔性體模型［8］.由于著陸沖擊過程中涉及材料、幾何和接觸等非線性問題，采用多體動力學建模方法很難將這些非線性因素考慮在內.例如考慮結構柔性時內外套筒接觸面法向力很復雜，而多體動力學模型內外套筒之間往往采用滑動副的約束形式，因此很難準確地計算著陸沖擊過程中內外套筒之間的摩擦力.著陸腿多柔性體動力學模型的柔性信息通常是以沖擊前著陸腿的構型和邊界條件給出的，在著陸沖擊過程中，著陸腿支柱內外套筒會產生壓縮行程，著陸腿構型和邊界條件是不斷變化的，用著陸沖擊前的構型和邊界條件生成的模態中性文件來分析著陸沖擊過程也會產生一定的模型誤差.此外，多體動力學模型中著陸腿足墊與月壤的接觸力只能根據具體工況采用經驗公式計算，通用性較差.

本文以非線性有限元理論為基礎，充分考慮著陸器著陸腿在著陸沖擊過程中的幾何、材料和接觸等非線性因素，建立了詳細的著陸腿有限元模型，并采用ABAQUS/Explicit作為求解器進行著陸沖擊非線性動力學分析，并與試驗數據進行了對比.仿真結果表明，非線性有限元動力學模型能較準確地預測著陸腿的著陸緩沖性能.

1 著陸腿的構型及緩沖原理

月球著陸器多采用腿式著陸緩沖機構，著陸腿圍繞著陸器中心軸均勻分布，如圖1所示.單個著陸腿緩沖機構由主支柱、輔助支柱和足墊組成.主支柱外筒上端通過萬向節與著陸器主體連接，主支柱內筒下端通過球鉸與足墊連接.輔助支柱通過萬向節著陸器主體連接，通過球鉸與主支柱連接.主、輔支柱內都安裝有鋁蜂窩芯子緩沖器，利用蜂窩芯子塑性壓縮變形吸收著陸沖擊過程中的動能，起到緩沖著陸沖擊載荷的作用.主支柱內的緩沖器具有單向緩沖功能，輔助支柱緩沖器具有雙向緩沖功能.

圖1 軟著陸機構示意圖

2 顯式非線性有限元分析理論

顯式非線性有限元動力學模型的數值解法，是將結構在空間域進行離散，把連續的微分方程轉換成有限階的代數方程組:

對求解的時間歷程在時間域內離散，并采用顯式積分方法進行求解.中心差分法是最常用的顯式積分方法，積分步驟如下:

其中，u·為速度列陣;u為位移列陣;上標(i)表示增量步的次數，(i-1/2)和(i+1/2)是指增量步的中間值.這樣，在增量步開始時提供了滿足動力學平衡條件的加速度.得到了加速度后，在時間上“顯式地”前推速度和位移.顯式積分算法中，不需要形成整體的剪切剛度矩陣，由于是顯式的前推模型的狀態，所以不需要迭代和收斂準則.顯式動力學求解方法是條件穩定的，最大穩定時間積分步長Δts與單元的特征尺寸Le和波速cd相關:

對于線彈性材料，cd的計算公式如下:

其中，E為彈性模量;ν為泊松比;ρ為密度.

3 著陸沖擊有限元建模

3.1 著陸腿有限元模型

在ABAQUS/CAE平臺上建立著陸腿有限元模型，模型主要包括鋁蜂窩緩沖器、主支柱、輔助支柱和足墊，如圖2所示.著陸腿支柱內外套筒采用S4R減縮積分殼單元及S3殼單元建模，并對不同區域賦予不同的單元截面屬性(section property).足墊采用解析剛體建模.輔助支柱和主支柱之間、主支柱與足墊之間采用球鉸連接單元(connector element)連接.

著陸腿中對仿真結果影響不大的細節已經做了簡化處理.由于著陸腿一些局部區域的單元尺寸較小，這些單元控制最大穩定時間增量步長，對這些單元較小的區域采用質量縮放技術，將這些局部區域單元的質量增加5倍，人為地增大材料的密度，由式(4)、式(5)可知，穩定時間步長可增加約2倍.這些局部區域質量的增大不會對著陸腿系統的總體動力學響應產生太大影響，但卻可以明顯地提高計算效率，減少計算量.

圖2 著陸腿有限元模型

在著陸沖擊過程中，著陸腿各支柱內外套筒接觸面之間以及足墊與著陸面之間的相互作用采用接觸算法來實現.模型采用ABAQUS/Explicit中的通用接觸算法定義著陸腿構件間的接觸，同時對不同的接觸區域定義不同的接觸屬性.采用庫侖摩擦模型來描述接觸面間摩擦的相互作用.摩擦系數定義如下:

其中，μ為摩擦系數;μk為動摩擦系數;μs為靜摩擦系數;dc為指數衰減系數;γ·eq為接觸面間的相對滑移速度.模型中著陸腿支柱內外套筒之間的摩擦參數取值均由試驗標定.

3.2 鋁蜂窩緩沖器模型

采用Crushable Foam體積硬化模型作為鋁蜂窩緩沖器的材料模型.根據鋁蜂窩緩沖器的額定壓縮載荷行程特性，定義材料模型的彈性及硬化參數.初始屈服應力由鋁蜂窩的壓縮載荷和鋁蜂窩芯子的橫截面積確定.將弱蜂窩極限壓縮塑性應變對應的屈服應力設為一個大值，當弱蜂窩達到極限壓縮行程后將會硬化，從而促使強蜂窩開始壓縮.

為了驗證模型的正確性，本文以主支柱二級鋁蜂窩緩沖器的載荷行程特性進行了仿真分析，分析模型如圖3所示.底部剛性板固支，蜂窩緩沖器固定在底板上，頂部剛性板以4 m/s的速度向下運動，達到蜂窩的極限壓縮行程時停止.底部剛性板的支反力(80 Hz濾波)以及鋁蜂窩的壓縮行程曲線如圖4所示.曲線中較平滑的兩段對應的壓縮載荷與設計值基本一致.整個壓縮過程中鋁蜂窩的總塑性耗散能為7 548 J，與額定值7 520 J相當.仿真結果證明，該模型能很好地模擬蜂窩緩沖器的緩沖及吸能特性.

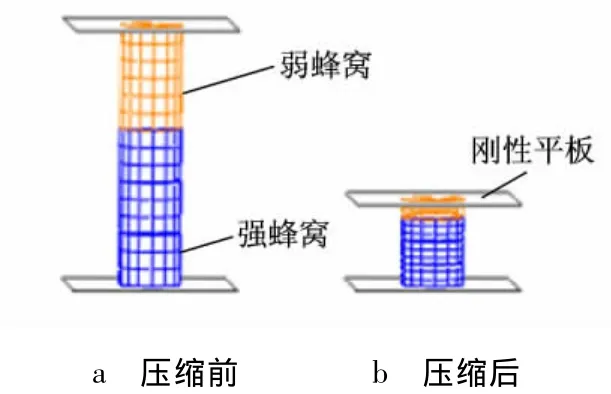
圖3 蜂窩緩沖器有限元模型

圖4 鋁蜂窩緩沖器載荷行程曲線

4 單腿著陸沖擊仿真及試驗驗證

單腿著陸沖擊試驗裝置如圖5所示.吊籃用于模擬著陸腿的真實安裝情況，吊籃安裝在導軌上，只能沿導軌在豎直方向運動，吊籃上安裝有配重用于模擬不同的著陸工況.試驗時，由起吊裝置將吊籃及著陸腿吊至指定高度后由釋放裝置釋放，吊籃及著陸腿在重力作用下沖擊到著陸平臺上.由安裝在吊籃上的加速度儀測量吊籃中心處的加速度.本文對表1中的著陸工況進行仿真分析，以驗證著陸腿模型的正確性.

圖5 單腿著陸沖擊試驗示意圖［7］

表1 著陸沖擊試驗工況

單腿著陸沖擊有限元仿真模型如圖6所示.模型由吊籃、著陸腿和著陸面組成.由于吊籃為鋼結構，其剛度比著陸腿大，且不是仿真研究所關注的重點，因此采用離散剛體模型建模，其邊界條件施加在離散剛體的質心參考點上，約束參考點上的3個旋轉自由度和y向、z向的平移自由度.著陸腿支柱和吊籃之間采用萬向節連接單元連接.著陸平臺分為剛性月面和模擬月壤兩種情況.采用Cap Drucke-Prager(CDP)模型作為模擬月壤的材料模型，該模型是在子午線為線性的Drucker-Prager模型上加上一個帽蓋屈服面形成的，這個帽蓋屈服面設置了靜水壓力的上限，因此提供了一個非彈性硬化機制用于描述材料的塑性壓縮.模型參數由JLU2模擬月壤［9］的三軸壓縮試驗數據及其相關研究成果標定，具體的模型參數如表2所示.表中，d為材料粘性;β為材料摩擦角;R為帽蓋偏心率;p0為帽蓋初始屈服面位置;r為過度面半徑參數;K為流動應力比.模擬月壤的壓縮系數Cc和膨脹系數Cs分別取0.02和0.005，月壤的壓縮硬化特性由壓縮系數、膨脹系數和初始孔隙率定義.

圖6 單腿著陸沖擊仿真模型

表2 模擬月壤材料屬性

著陸沖擊仿真結果與試驗結果的對比如表3所示，著陸腿主支柱和輔助支柱的緩沖器的緩沖行程仿真結果與試驗結果基本一致，兩個工況的誤差都在工程上可接受的范圍內.這說明非線性有限元模型可以較準確地預測著陸腿的緩沖和吸能特性.工況2的主支柱行程仿真值要比工況1小，這是因為模擬月壤的塑性變形會吸收一部分動能;而工況2主支柱行程試驗值卻比工況1大，原因主要有以下兩方面:蜂窩芯子由于存在制造誤差，工況2所用蜂窩芯子實際壓縮載荷可能要比工況1所用的蜂窩芯子小;試驗中工況1所用鋁蜂窩芯子存在壓偏的現象，這會增大著陸腿套筒間摩擦力，使得工況1的壓縮行程偏小.

為了研究著陸腿的柔性對著陸沖擊性能的影響，在工況1條件下［8］，對著陸腿施加剛性約束進行著陸沖擊仿真分析，吊籃中心加速度(80 Hz濾波)時間歷程如圖7所示.吊籃中心加速度試驗峰值約為9.18 g，柔性著陸腿模型和剛性著陸腿模型仿真結果分別為8.0 g和7.67 g.由于試驗過程中加速度測量點的測試結果受安裝剛度影響較大，而仿真模型的吊籃采用剛體建模，導致加速度試驗值和仿真值匹配性不是很好，但總體變化趨勢基本一致.同時由圖7可知，柔性腿模型比剛性腿模型的仿真值更接近試驗測試值.

柔性腿和剛性腿主支柱內外套筒之間的摩擦力(80 Hz濾波)如圖8所示.柔性腿套筒摩擦力峰值約為5.4 kN，剛性腿峰值約為4.36 kN.剛性腿主支柱套筒間的摩擦力變化比較平緩，柔性腿主支柱摩擦力的波動性較大，這主要是主支柱本身，以及輔助支柱的彈性變形引起的.在著陸沖擊前0.15 s過程中，柔性腿摩擦力曲線大部分都位于剛性腿摩擦力曲線上方，可見著陸腿的柔性變形會增大套筒間的摩擦力.

工況2著陸沖擊仿真能量時間歷程如圖9所示.在著陸沖擊后0.15 s時刻，系統動能變化量、重力做功及人工應變能總和為4 135 J，塑性變形和摩擦力耗散能總和約為4 077 J，相差的58 J由數值求解過程中引入的粘性耗散掉，由此可見，沖擊過程中能量的變化符合能量守恒定律.人工應變能很小說明仿真模型沒有發生明顯的沙漏現象，仿真結果是可靠的.系統著陸時刻理論初始動能為3367 J，仿真分析初始時刻動能為3384 J，這是由于采用了局部質量放大技術引起的，這個微小的差異對著陸腿的整體沖擊動力學響應的影響不大，但使穩定時間步長由原來7.08×10-7s增大到1.46×10-6s，顯著地提高了計算效率.

表3 仿真結果與試驗結果對比

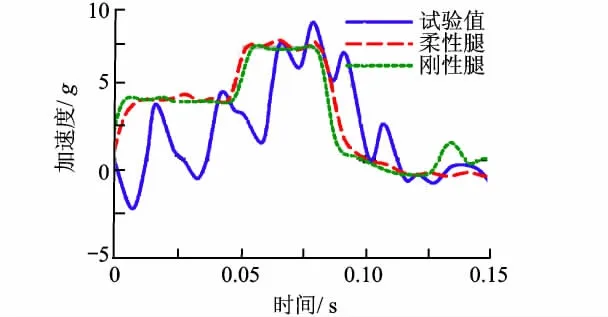
圖7 單腿著陸沖擊仿真模型

圖8 主支柱內外套筒間的摩擦力時間歷程

圖9 工況2能量時間歷程

5 結論

1)非線性有限元動力學建模方法可以充分考慮著陸腿著陸沖擊過程中的材料、幾何、接觸等非線性因素，能較準確地預測著陸腿的載荷緩沖和吸能特性，可用于指導著陸腿設計及優化.

2)著陸腿柔性對其內外套筒之間的摩擦力有較大的影響，分析時應予以考慮;增加著陸腿剛度可以減小摩擦力.

3)采用局部質量縮放技術可以顯著地增大顯式動力學程序的穩定時間增量步長，提高計算效率，且不會對總體動態響應產生太大影響.

References)

［1］ William F R.Apollo experience report-lunar module landing gear subsystem［R］.NASA TN D-6850，1972

［2］ Merchant D H，Sawdy D T.Monte Carlo dynamic analysis for lunar module landing loads［J］.Journal of Spacecraft and Rockets，1970，8(1):48-55

［3］ Doiron H H，George A Z.Apollo lunar module landing dynamics［C］//The 41st Structures，Structural Dynamics，and Materials Conferenceand Exhibit.Washington:AIAA/ASME/ASCE/AHS/ASC，2000

［4］ Andrew L B，James R C，Ralph D L，et al.Planetary landers and entry probes［M］.New York:Cambridge University Press，2007

［5］ Masahiro N，Akira M.Modeling for lunar lander by mechanical dynamics software［C］//Modeling and Simulation Technologies Conference and Exhibit.Washington:AIAA，2005

［6］ Hilchenbach M，Kuchemann O，Rosenbauer H.Impact on a comet:Rosetta lander simulations［J］.Planetary and Space Science，2000，48(5):361-369

［7］朱汪，楊建中.月球探測器軟著陸機構著陸腿模型與仿真分析［J］.宇航學報，2008，29(6):1723-1728 Zhu Wang，Yang Jianzhong.Modeling and simulation of landing leg for lunar landing gear system ［J］.Journal of Astronautics，2008，29(6):1723-1728(in Chinese)

［8］ 曾福明，楊建中，朱汪，等.月球著陸器著陸緩沖性能研究［J］.航天器工程，2010，19(5):43-49 Zeng Fuming，Yang Jianzhong，Zhu Wang，et al.Research on landing impact attenuation performance of lunar lander［J］.Spacecraft Engineering，2010，19(5):43-49(in Chinese)

［9］楊艷靜.模擬月壤和月球車車輪相互作用的數值仿真和試驗研究［D］.北京:中國空間技術研究院，2010 Yang Yanjing.Numerical and experimental research of lunar soil stimulant and lunar rover wheel interaction［D］.Beijing:China Academy of Space Technology，2010(in Chinese)