基于相關分析和組合神經網絡的退化預測

黨香俊 姜同敏

(北京航空航天大學 可靠性與系統工程學院，北京100191)

對性能退化的有效預測是加速退化試驗和故障預測與健康管理領域的關鍵技術.在故障預測與健康管理中，對系統關鍵部件剩余壽命的準確預測能夠有效預防系統事故的發生，使工程人員根據系統運行情況合理規劃和實施維修計劃，從而避免過度維修，降低壽命期內的維修成本.而對于加速退化試驗，退化軌跡的長距離有效預測，意味著退化試驗不需要進行到產品故障或接近于故障，使得試驗時間顯著減少，試驗成本大幅降低.尤其是對于產品本身昂貴并且研究進度緊張的情況，這一作用更加明顯.

為了滿足工程實際的需要，越來越多的研究人員開始關注這一領域，并且應用不同理論提出了一些預測模型.從現有的文獻來看，預測模型主要可以分為基于物理的模型、基于知識的模型和數據驅動的模型三大類.基于物理的方法通常使用由直接或間接影響相關組件健康狀態的物理過程抽象出的數學模型，模型的建立需要豐富的專業知識，并且模型的參數驗證需要大量實際數據，成本過高［1-3］.基于知識的方法利用產品所屬領域內的各種歷史信息進行預測，雖然不再需要物理模型作為假設，但對信息量的要求過高［4］.數據驅動的方法基于統計和學習技術，可以分為基于統計的方法和基于人工智能的方法.基于統計的方法以統計理論為基礎，主要應用貝葉斯理論和隨機過程理論及其演變形式進行建模［5-7］.基于人工智能的預測方法，以采集到的性能數據作為輸入，應用神經網絡模型及其演變形式進行預測.神經網絡不需要預先做出輸入條件假設和統計模型，顯著簡化了模型的建立過程.此外，神經網絡模型對輸入數據的要求低，對于其他方法難以處理的非線性、高階、時變動態和一些不具有分析模型的復雜過程，也都具有很好的處理能力.文獻［8］根據故障發展的多變量趨勢，應用自組織神經網絡預測了軸承系統的剩余壽命.文獻［9］以最小量化誤差為指標，采用自組織映射圖和BP(Back Propagation)神經網絡對滾珠軸承的剩余壽命進行了預測.文獻［10］基于傳感器信號，使用動態小波神經網絡計算并連續更新組件的剩余壽命分布.

在實際預測中，性能退化預測方法主要還需要在以下兩個方面做出改進:①復雜數據預測的準確性有待提高.對復雜的退化數據，預測結果有時會與真實值存在較大差距.②預測的距離需要提升.預測的有效距離是影響退化預測作用范圍的重要因素，較長距離的壽命預測能夠為預防性維修決策提供更大的便利.

為了解決上述問題，本文提出了一種以相關分析和組合神經網絡為基礎的退化預測方法.首先，根據退化數據的特點，選擇合適的參數對原始數據進行小波變換，降低退化數據的復雜性.其次，對變換后的序列，采用Durbin-Watson檢驗和偏相關圖進行相關分析，檢驗小波變換參數選擇的合理性.最后，根據小波變換后序列的特點，組合BP和小波神經網絡進行退化預測.為了驗證方法的適用性，本文對某電子產品的實際退化數據進行了預測，最后給出與單獨采用小波神經網絡方法的對比分析.

1 小波變換與相關分析

為了獲得較好的預測結果，本文采用小波變換將復雜數據分解成一系列簡單的子序列，而子序列所具有的規律性是影響預測效果的關鍵因素.因此，對分解后的子序列進行自相關分析是必不可少的.

1.1 離散小波變換

設采集到的信號 Hjf為能量有限信號 f∈L2(R)在分辨率2j下的近似，則Hjf可以進一步分解為f在分辨率2j-1下的近似Hj-1f，以及位于分辨率2j-1相應的細節Dj-1f之和.

設φ與ψ分別為尺度函數和小波函數，則信號f在分辨率2j-1下近似Hj-1F和細節Dj-1f分別假設為

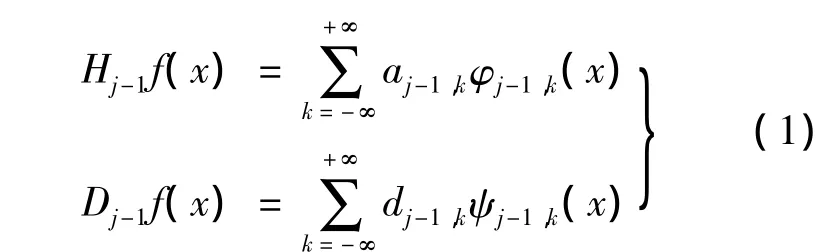
其中aj-1k與dj-1k分別為分辨率2j-1下粗糙系數與細節系數，而分辨率2j下信號f的近似Hjf可以直接寫成

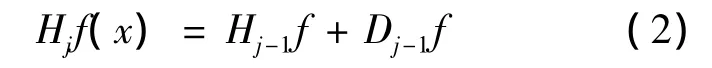
以此類推，信號Hjf可繼續進行多級分解，如圖1所示.

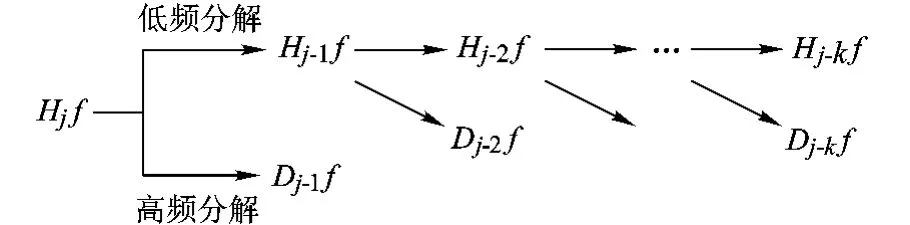
圖1 信號分解

將式(1)代入式(2)，結合圖1所示的多級分解結構，可得到如下多級分解算法:

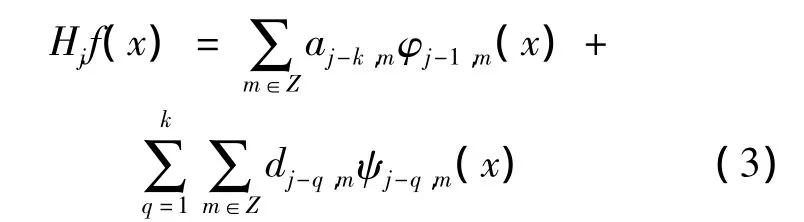
信號重構是分解的逆算法，重構過程如圖2所示.

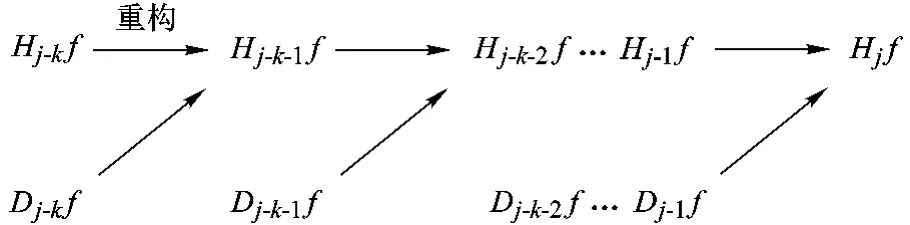
圖2 信號重構

1.2 自相關分析

1.2.1 Durbin-Watson檢驗

影響時間序列預測效果的主要因素是未來數據對已有數據的依賴性，即序列的前期數據包含后期數據特征信息的多少.若序列具有較高的自相關性，則應用預測模型進行預測時將獲得更好的預測效果.Durbin-Watson檢驗是一種常用的自相關分析方法，其計算簡單，結果直觀.對時間序列{x(t)}，Durbin-Watson統計量由下式計算:

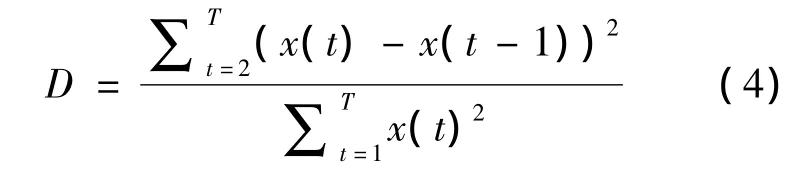
其中T為時序長度.如果時間序列{x(t)}不存在自相關性，D應趨近于2.若D為0，表明存在完全的正自相關;若D為4，則表明存在完全負相關.{x(t)}的正或負相關程度，可以由D與0或4的接近程度來判斷.

1.2.2 偏相關圖

由下式定義偏自相關函數φkk，當然也是作為過程自相關函數ρk的函數.

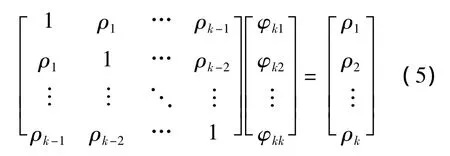
由上式定義的φkk稱為過程{x(t)}滯后k的偏相關，是x(t)和x(t-k)在扣除了中間變量x(t-1)，x(t-2)，…，x(t-k+1)的影響滯后的偏相關.

2 組合神經網絡

2.1 BP神經網絡

BP神經網絡是一種采用BP算法的多層感知器神經網絡模型，它由輸入層、中間層和輸出層組成.中間層也就是隱含層，可以是一層或多層.圖3是一個具有三層網絡結構的簡單BP神經網絡模型，其中間層為一層.

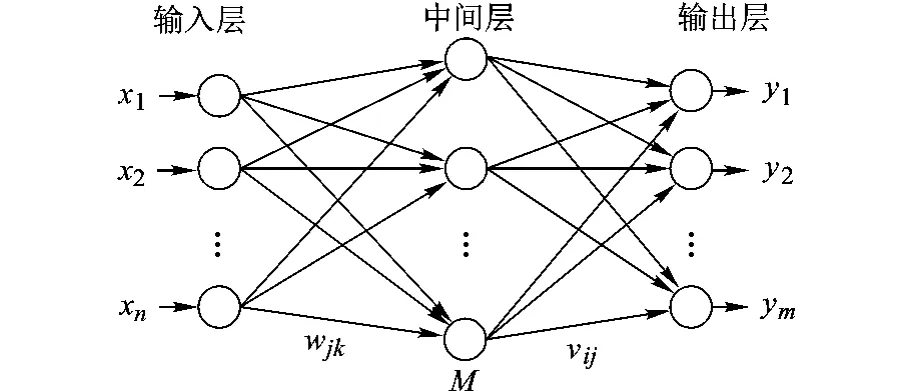
圖3 三層BP神經網絡

其中，(x1，x2，…，xn)為 n 維輸入向量;(y1，y2，…，ym)為m維輸出向量;wj，k為輸入層節點k與隱含層節點j之間的連接權值;M為隱含節點神經元個數;vij為隱含層節點j與輸出層節點i之間的連接權值.

BP神經網絡各隱層節點的激活函數使用Sigmoid函數(S函數).單極S函數可表示為

多輸入單輸出BP神經網絡輸入輸出關系為

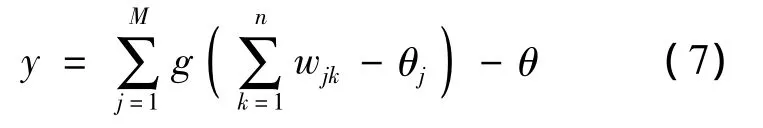
其中，θj為隱含層節點j的閾值;θ為輸出層節點的閾值.

2.2 小波神經網絡

小波神經網絡［11］融合了小波變換與神經網絡，將常規神經網絡隱含層節點函數由小波基函數代替，相應的輸入層到隱含層的權值及閾值分別由小波函數的尺度與平移參數代替，同時具備了小波變換的局部化能力和神經網絡的自適應學習功能.小波神經網絡輸入與輸出函數關系為

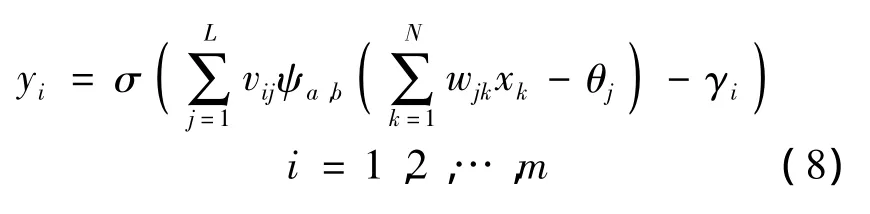
其中，xk為輸入層的第k個神經元的輸入;N為輸入層節點神經元個數;γi為輸出層i節點的閾值;L為隱含層節點數;m為輸出層節點數.

產品退化預測主要以實際使用或試驗中監測獲得的退化數據預測監測時間點之后的性能指標.由于輸入輸出均為退化量值，預測過程中網絡不存在輸出延遲，故小波神經網絡隱含層和輸出層節點的閾值項可以省略，θj=0，γi=0.式(8)可以相應簡化為

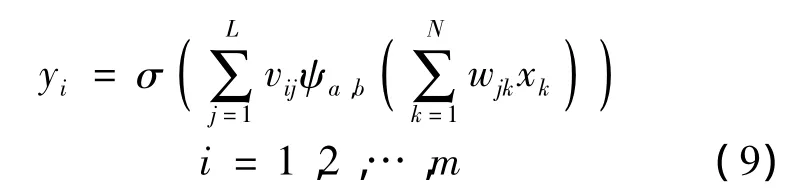
2.3 組合神經網絡

根據離散小波分解后多級序列所具有的變化特點，選擇BP神經網絡和小波神經網絡對不同子序列分別進行預測.式(3)中右邊第一項用BP神經網絡處理，第二項用小波神經網絡預測.具體地，用式(7)和式(9)分別替換式(3)中對應項，同時去除各層節點的閾值，可得組合神經網絡的預測公式:

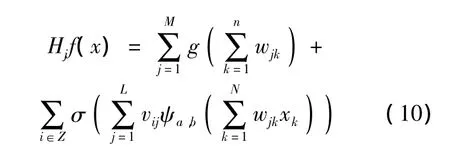
3 退化預測應用驗證

上文對BP和小波組合神經網絡用于產品性能退化數據預測的理論模型進行了推導，而模型在工程中的適用性尚未得到驗證.為此，下面將利用某電子產品在工作應力下的退化監測數據進行退化預測的驗證研究.

對該產品進行的退化試驗期間共采集到了500×102min的退化數據，以其中前300×102min退化數據作為預測模型的原始數據，如圖4所示.

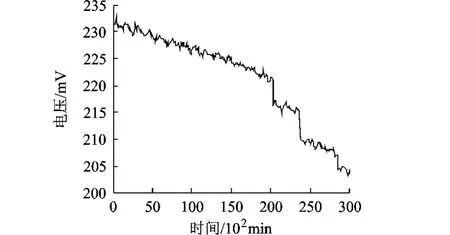
圖4 原始退化數據

從圖4可以看出，原始數據的退化趨勢變化不規律，在 200×102，240×102和290×102min附近發生了明顯的突變，并且變化幅度較大.若直接對原始數據進行預測，則對預測模型要求過高，傳統預測方法很難直接給出滿意的結果.為了降低退化軌跡的復雜性，本文對原始數據首先進行離散小波變換，其變換后的細節序列如圖5所示.

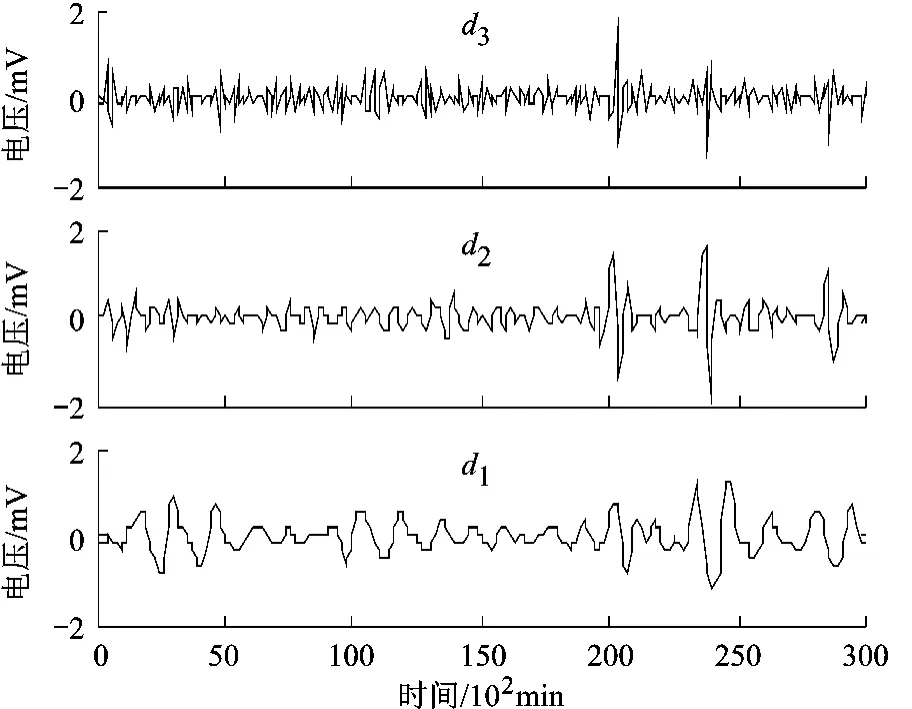
圖5 細節序列

與原始數據相比，離散小波變換后的細節序列具有較低的復雜程度，并且表現出一定的規律性.序列中前期數據包含后期數據信息量的大小，將會直接影響后續的預測效果.根據式(4)，計算子序列的Durbin-Watson統計量，結果見表1.

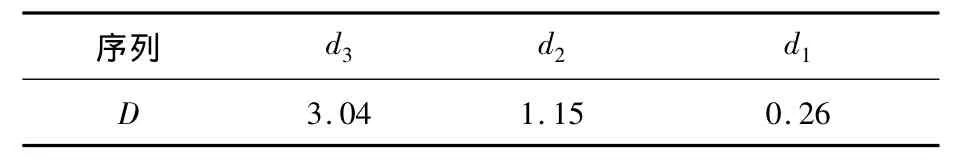
表1 Durbin-Watson統計量

由表1中可見，d3序列的D值大于2，其序列一階相關性為負，但由于D值與4之差在0～2之間，并不能以此判斷序列是否具有相關性.d2序列的D值小于2，其序列一階相關性為正，但由于D值位于0與2之間，不能確定序列是否具有相關性.d1序列的D值接近于0，故序列具有一階正相關性.Durbin-Watson檢驗沒能對子序列d3和d2的自相關程度作出明確的判定，下面應用偏相關圖對序列作進一步分析，給出自相關性的直觀判斷，如圖6～圖8所示.

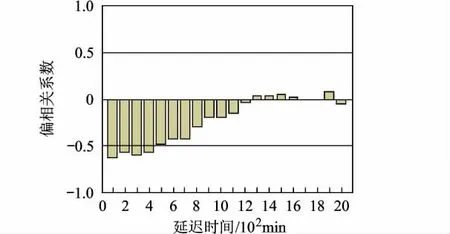
圖6 d3偏相關圖

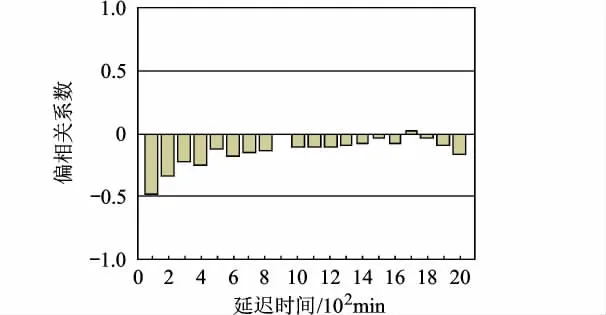
圖7 d2偏相關圖

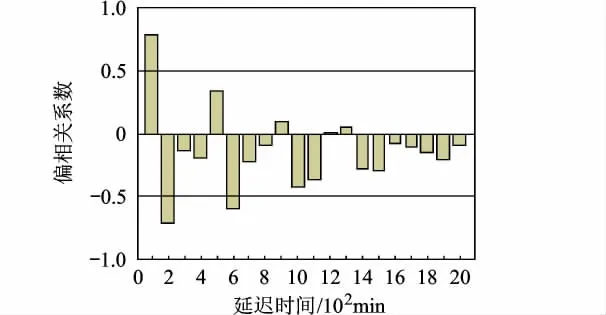
圖8 d1偏相關圖

從圖6中可以看出，d3序列具有一、二階負相關性，也驗證了Durbin-Watson檢驗所判定的一階相關性為負的結論.圖7表明，雖然d2的一階偏相關系數為負，與表1判斷的相關性可能為正矛盾，但由于其偏相關系數較小，故d2不具有相關性.上文應用Durbin-Watson檢驗法判定了d1序列具有一階正相關性，這一結論在圖8中得到直觀的驗證.另外，除了一階相關性，d1還具有較強的二階負相關性.

離散小波變換在降低原始數據復雜性的同時，也使得子序列具有較好的自相關性，減小了后續序列預測的困難.下面采用BP網絡與小波神經網絡相結合的方法，應用前文推導的組合神經網絡式(10)，對產品300×102min之后的退化軌跡進行預測.根據實際退化數據的特點，設定式(10)中相應的模型參數，得

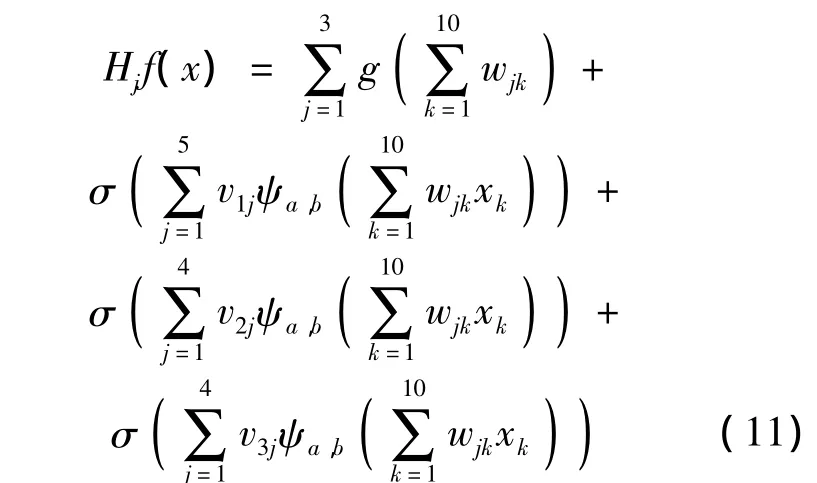
其中網絡隱層節點函數g(·)選用式(6)所示的S函數，隱層節點函數 ψa，b選擇 Morlet小波.

為了縮短網絡學習時間，提高收斂速度，本文采用L-M(Levenberg-Marquardt)法作為網絡的學習訓練算法.L-M法是一種結合了高斯-牛頓法和梯度下降法優點的快速算法，其基本思想是使其每次迭代不再沿單一的負梯度方向，而是允許誤差沿著惡化的方向進行搜索，同時通過在最速梯度下降法和高斯-牛頓法之間自適應調整來優化網絡權值，使網絡能夠有效收斂，提高了網絡的收斂速度和泛化能力.

對于預測效果的驗證，采用結合小波去噪的小波神經網絡方法與本文提出的組合神經網絡方法進行對比分析.將兩種方法的預測結果分別與實際數據進行比較，如圖9和圖10所示.

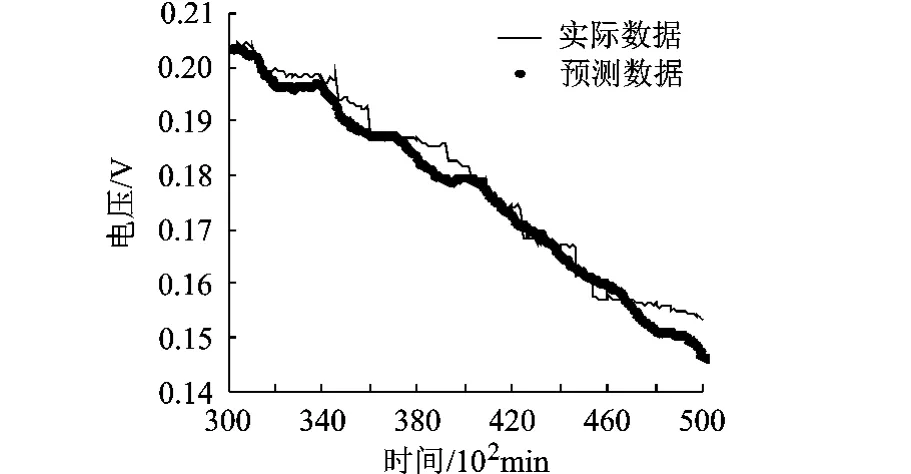
圖9 小波神經網絡預測結果

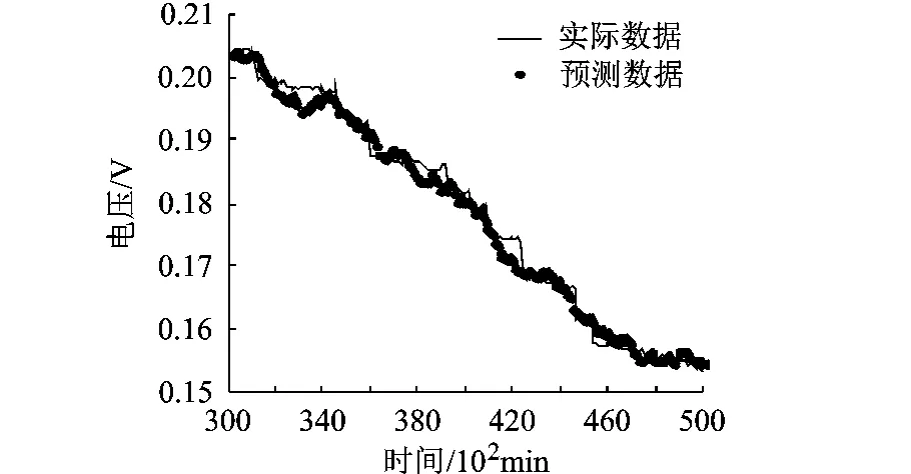
圖10 組合神經網絡預測結果

為了評價預測軌跡與實際退化軌跡的符合程度，引入均方誤差(MSE，Mean Square Error)作為評價指標:

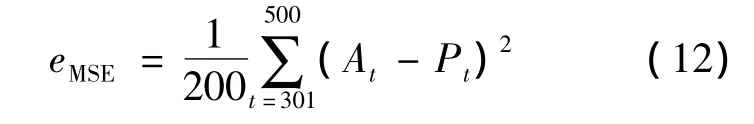
其中At和Pt為退化數據的實際值和預測值.

根據產品失效的歷史信息，選擇產品的失效閾值為0.16V，則產品從第301×102min開始，到退化軌跡首次穿越0.16 V所經歷的時間即為產品的剩余壽命.剩余壽命(RUL，Remaining Useful Life)預測值與真實值計算結果如表2所示.

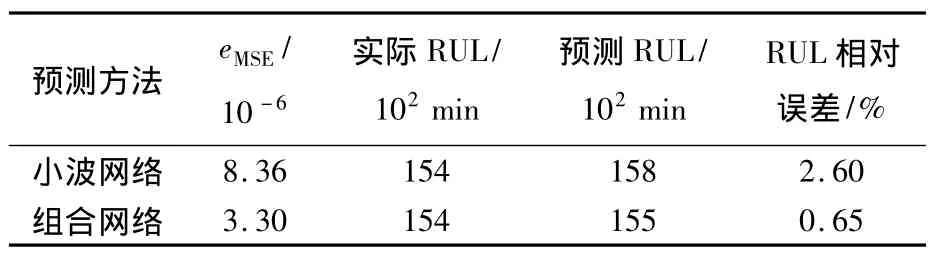
表2 均方誤差及剩余壽命對比分析

從以上預測結果可以看出，本文所提組合神經網絡方法與單純采用小波神經網絡方法相比，對退化軌跡預測的MSE更小，對剩余壽命的預測精度更高.另外，對比圖9和圖10中460×102min以后的退化軌跡，小波神經網絡的預測結果已經偏離了實際數據的退化趨勢，不能給出更長期的預測，而組合神經網絡則給出了良好的預測軌跡，具有更長的有效預測距離.

4 結論

本文提出了相關分析和組合神經網絡相結合的退化預測方法，并對某電子產品退化數據進行了實際預測驗證.主要結論如下:①離散小波變換和自相關分析提供了一種將復雜退化數據，分解成相對簡單的有序子序列的途徑.②BP和小波神經網絡構成的組合神經網絡，可以有效發揮兩種網絡各自的優勢，對實際退化序列具有良好的預測效果，具有良好的工程應用前景.

References)

［1］ Luo J，Bixby A，Pattipati K，et al.An interacting multiple model approach to model-based prognostics［C］//Proceedings of the IEEE International Conference on Systems，Man and Cybernetics.New York:Institute of Electrical and Electronics Engineers Inc，2003:189-194

［2］ Byington C S，Watson M，Edwards D，et al.A model-based approach to prognostics and health management for flight control actuators［C］//2004 IEEE Aerospace Conference Proceedings.New York:Institute of Electrical and Electronics Engineers Inc，2004:3351-3362

［3］周玉輝，康銳，蘇荔，等.基于加速磨損試驗的止推軸承磨損壽命預測［J］.北京航空航天大學學報，2011，37(8):1016-1020 Zhou Yuhui，Kang Rui，Su Li，et al.Life prediction of thrust bearings based on accelerated wear test［J］.Journal of Beijing University of Aeronautics and Astronautics，2011，37(8):1016-1020(in Chinese)

［4］ Biagetti T，Sciubba E.Automatic diagnostics and prognostics of energy conversion processes via knowledge based systems［J］.Energy，2004，29(12-15):2553-2572

［5］ Liu Y，Li S Q.Decision support for maintenance management using Bayesian networks［C］//2007 International Conference on Wireless Communications，Networking and Mobile Computing.New York:Institute of Electrical and Electronics Engineers Inc，2007:5708-5711

［6］ Dong M，He D.Hidden semi-Markov model-based methodology for multi-sensor equipment health diagnosis and prognosis［J］.European Journal of Operational Research，2007，178(3):858-878

［7］王小林，程志君，郭波.基于維納過程金屬化膜電容器的剩余壽命預測［J］.國防科技大學學報，2011，33(4):146-151 Wang Xiaolin，Cheng Zhijun，Guo Bo.Residual life forecasting of metallized film capacitor based on wiener process［J］.Journal of National University of Defense Technology，2011，33(4):146-151(in Chinese)

［8］ Zhang S，Ganesan R.Self-organizing neural networks for automated machinery monitoring systems［J］.Mechanical Systems and Signal Processing，1996，10(5):517-532

［9］ Huang Runqing，Xi Lifeng，Li Xinglin，et al.Residual life predictions for ball bearings based on self-organizing map and back propagation neural network methods［J］.Mechanical Systems and Signal Processing，2007，21(1):193-207

［10］ Gebraeel N Z，Lawley M A.A neural network degradation model for computing and updating residual life distributions［J］.IEEE Transactions on Automation Science and Engineering，2008，5(1):156-163

［11］ Zhang Q，Benveniste A.Wavelet networks［J］.IEEE Transactions on Neural Networks，1992，3(6):889-898