圓鋼管混凝土框架結構節點填充混凝土性能分析★

宋彬彬

(湖南理工學院，湖南岳陽 414006)

0 引言

在組合結構類型中，圓柱鋼管混凝土結構應用越來越廣泛，由于其充分利用了鋼材抗拉強度與混凝土材料的抗壓強度，使兩種材料在抵抗荷載與作用過程中充分發揮出其材料特性，且圓柱使內填混凝土處于三向受壓而具備較高的承載能力。在圓柱鋼管混凝土結構中，節點處的受力及變形均較為復雜，若能對節點的性能深入研究則有助于更好地掌握圓柱鋼管混凝土結構的力學性能。本文通過分析四個圓柱鋼管混凝土結構梁柱節點局部模型的試驗結果，得到了圓柱內填充混凝土的應變分布規律以及構件破壞特征，此外還采用有限元數值分析方法進一步分析圓柱鋼管內填充混凝土的應變分布規律，對數值分析結果與試驗分析結果進行比較。

1 節點的簡化

試驗研究對象采用兩種模型，分別考慮無橫隔板加強及有貫通橫隔板加強兩種情況，加載方式分為單向及雙向兩種。其中UMN表示單向加載無橫隔板節點，BMN表示雙向加載無橫隔板節點，而UMD表示單向加載有貫通橫隔板加強節點，BMD表示雙向加載有貫通橫隔板加強節點。由于填充混凝土本身的材料性能使之在鋼梁翼緣受壓端可承擔較大壓力，因此，分析對象只取受拉翼緣部分可行且能夠使分析過程得到簡化。設定不同構件尺寸作為多個節點局部模型且施加荷載，荷載類型采用單向加載及雙向加載兩種方式，在兩種荷載作用下，可觀察填充混凝土的應變分布及破壞規律，從而考察節點混凝土的破壞特征。

2 加載及測定方法

單向荷載作用在梁翼緣端部位置且為拉力;雙向荷載則一邊在梁翼緣處施加拉力，一邊在垂直方向的另一端梁翼緣處施加壓力，并且拉伸及壓縮荷載均按比例進行增減，同時保證在整個加載過程中互相垂直的兩個方向上荷載絕對大小值相同。雙向荷載作用導致構件開始發生破壞時，拉力維持不變，繼續施加壓力直到構件達到其極限承載力而產生最終破壞。在各個試件的柱填充混凝土內相應位置處放置應變片即可測量出填充混凝土的應變值，本文用C1來表示在柱鋼管管壁處且與拉力方向垂直的位置，用C2來表示位于柱截面中心處且沿拉力方向的位置，通過C1及C2處測得的應變數據即可了解該處的混凝土力學性能。

3 填充混凝土的應變分布

以通過應變片測出的混凝土應變值大小為橫坐標，試驗施加的相應荷載值大小為縱坐標繪制出圓柱內填充混凝土的相應曲線，如圖1，圖2所示。

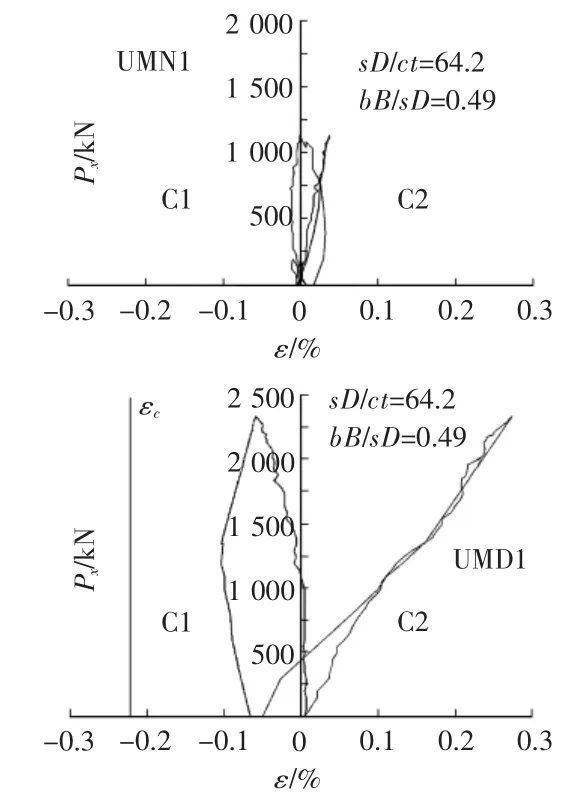
圖1 單向受力試件的混凝土荷載—應變試驗結果

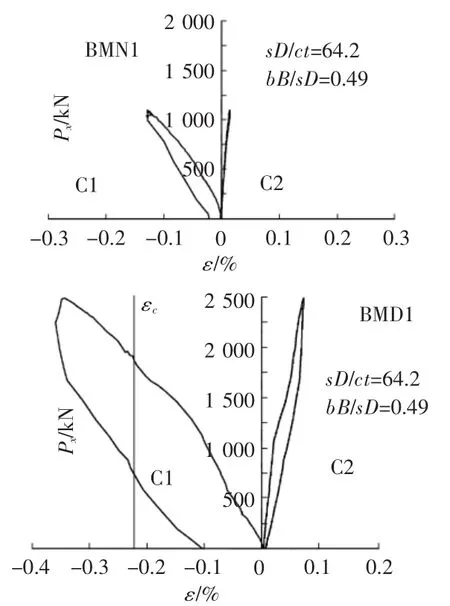
圖2 雙向受力試件的混凝土荷載—應變試驗結果

由圖1可見，在單向拉力作用下，無橫隔板加強試件UMN1及有貫通橫隔板加強試件UMD1在C1(柱鋼管管壁處且與拉力垂直方向)處受壓，在C2(柱截面中心處且沿拉力方向)處受拉。其中UMN1的拉應變及壓應變均小于0.1%且壓應變相差程度較大，表明受拉、受壓混凝土均未達到其極限應變值。而對于采用貫通橫隔板加強的試件UMD1，其在C2處的拉應變值已經接近0.3%，超過了基于混凝土材料拉壓試驗所得的最大值0.22%，其在C1處的壓應變值也遠較UMN1大，已經接近0.1%，但受拉應變及受壓應變都尚未達到混凝土的極限應變值。節點處混凝土沒有明顯破壞，仍可看作處于彈性階段，節點發生破壞主要體現在裂縫沿著焊縫處發展。

由圖2可見，在雙向荷載作用下，無橫隔板加強試件BMN1及有貫通橫隔板加強試件BMD1在C1(柱鋼管管壁處且與拉力垂直方向)處仍受壓，在C2(柱截面中心處且沿拉力方向)處仍受拉。雙向試件拉應變值小于單向試件拉應變值且拉應變大小并非隨拉力增大而增大，而是與鋼管外徑與壁厚的比值大小有關，鋼管徑厚比越小則拉應變越大，觀察多個試件發現鋼管徑厚比接近25的試件其拉應變可超過0.5%。BMD1與BMN1在加載卸載過程中的壓應變變化曲線形狀較為相似，且雙向試件的壓應變值均大于單向試件的壓應變值。BMD1的壓應變值接近0.4%，已超過混凝土的極限壓應變，但混凝土沒有發生破壞。部分雙向試件是由于梁先屈服而造成節點破壞。

4 試件的破壞特征

無橫隔板加強的試件UMN1及BMN1最終破壞并非由于混凝土達到其極限承載力，而是由于裂縫首先在梁翼緣與柱鋼管焊接處產生且沿著柱鋼管的軸向逐漸擴展，造成鋼管抗拉承載力不足從而使得節點喪失其承載能力。并且鋼管由于受力而向外凸起，平面外變形總體呈現出橢圓形形狀。而有貫通橫隔板加強的試件UMD1及BMD1最終破壞則主要是由于梁翼緣與橫隔板連接處的局部破壞造成的，裂縫首先在梁翼緣與橫隔板連接處產生，逐漸沿橫隔板向柱鋼管中心發展，從而造成柱鋼管管壁受拉且向外凸出，同樣表現出橢圓形平面外變形形狀。取出試件中的填充混凝土，可觀察到在受拉翼緣側的柱填充混凝土上留下了較為明顯的橢圓形的痕跡，在受壓翼緣側的柱填充混凝土上同樣也可觀察到比較明顯的橢圓形痕跡，從而進一步佐證了柱鋼管的平面外變形。通過觀察發現，填充混凝土并未出現開裂情況，這與試驗分析的填充混凝土應變分布規律一致。

5 有限元分析

5.1 單元類型及材料

根據對稱及簡化原則，取試件的1/8進行計算且在邊界處依據對稱面條件施加約束，按比例相應施加荷載。將柱鋼管、梁翼緣及填充混凝土均看作八節點彈塑性實體計算單元Solid45可以較好地模擬實際情況，分析中不可忽略焊縫的影響，因此對焊縫也設為Solid45;在受荷過程中，柱內填充混凝土與柱鋼管管壁之間會產生脫離，用三維面—面接觸單元Conta174和Targe170來考慮這一情況;忽略填充混凝土與鋼管間的粘結與摩擦。梁翼緣和柱管壁采用的鋼材其應力—應變關系為多線性模型且鋼材以及焊縫的材料屈服準則采用Von Mises準則;柱內的填充混凝土其應力—應變關系為雙線性模型，屈服準則則采用Drucker-Prager屈服準則。

5.2 有限元結果及分析

通過有限元分析同樣可得到填充混凝土的荷載—應變關系，以混凝土應變值大小為橫坐標，施加的相應荷載值大小為縱坐標繪制出圓柱內填充混凝土的相應曲線，如圖3，圖4所示。觀察可知，所有試件在C1(柱鋼管管壁附近且與拉伸荷載垂直方向)處受壓，在C2(鋼管中心處且沿受拉梁翼緣軸向方向)處受拉。單向試件UMN1的應變圖形與試驗結果較為接近，拉壓應變值均比較小;UMD1的拉應變值接近于0.25%，與試驗結果較為類似，但壓應變值較小，與試驗結果相比絕對值大小偏低，造成結果有微小誤差的原因可能是材料參數的選取不夠準確以及在數值分析時接觸分析與實際情況有誤差。

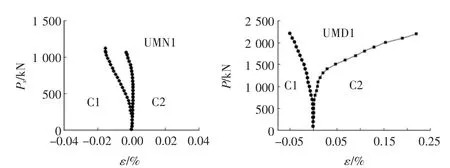
圖3 單向受力試件的混凝土荷載—應變有限元結果

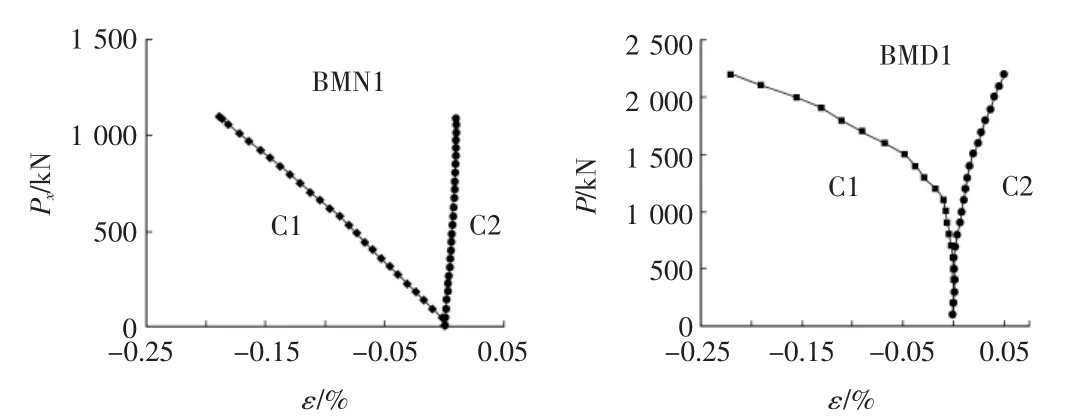
圖4 雙向受力試件的混凝土荷載—應變有限元結果

雙向試件的應變圖形形狀與試驗結果較為接近，且拉應變數值都比較小，均未超過0.1%，但壓應變值均比較大。BMN1的壓應變已經接近0.2%，而BMD1的壓應變值則已達到0.22%，但與試驗結果相比偏小。數值分析結果表現出對雙向試件而言，是否設置貫通橫隔板對柱鋼管的內填混凝土應變影響并不大。對圖1～圖4進行綜合比較分析可知，數值分析結果與試驗結果相比誤差不大，可見采用有限元分析來模擬試驗是可行的。

6 結語

本文采用試驗結果分析及數值分析兩種方法分析了四個圓柱鋼管混凝土梁柱節點模型在單向、雙向兩種加載情況下的柱填充混凝土的變形規律，并將試驗結果與數值分析結果進行比較，得出結論，用有限元模擬試驗是可行的，其誤差較小，可以較好地保證準確性。

［1］任啟輝.ANSYS7.0工程分析實例詳解［M］.北京:人民郵電出版社，2003.

［2］葉先磊，史亞杰.ANSYS工程分析軟件應用實例［M］.北京:清華大學出版社，2003.

［3］森田耕次.コンクリート充てん角形鋼管柱—鐵骨はり結合部的內ダイアフラム補強に關する研究［J］.日本建筑學會構造系論集，1991(4):13-15.

［4］付功義，森田耕次.コンクリート充填角形鋼管柱—合成梁偏心部分骨組架構の力學的舉動［A］.第2回鋼構造年次論文報告集［C］.1994:315-322.

［5］付功義，森田耕次.コンクリート充填圓形鋼管柱—鐵骨梁立體部分骨組架構における柱梁結合部の力學舉動に關する研究［A］.日本建筑學會構造系論文集［C］.1998:157-164.

［6］劉 兵.圓形鋼管混凝土結構梁柱節點抗彎強度的研究［D］.上海:上海交通大學碩士學位論文，2003.

［7］虞曉文.貫通橫隔板加強圓形鋼管混凝土柱—H型鋼梁節點局部抗彎強度的研究［D］.上海:上海交通大學碩士學位論文，2004.