中間設(shè)站法三角高程測量在沉降觀測中的應(yīng)用★
李捷斌 劉 忠 梁 磊
(1.陜西工業(yè)職業(yè)技術(shù)學(xué)院,陜西 咸陽 712000;2.長安大學(xué)地測學(xué)院,陜西 西安 710000)
0 引言
傳統(tǒng)的建筑物沉降觀測方法是采用幾何水準(zhǔn)測量。但該方法作業(yè)效率低,且施工場地環(huán)境等因素影響較大、作業(yè)危險。三角高程測量具有高差測定速度快、受地形條件限制小等優(yōu)點,特別適合在地形較復(fù)雜的地區(qū)進(jìn)行高程測量,但測量精度不及水準(zhǔn)測量。隨著測量技術(shù)的高速發(fā)展,高精度全站儀測角、測距精度都有了很大提高,三角高程精度也有了提升。本文探討了在小范圍內(nèi),精密三角高程測量應(yīng)用于建筑物沉降的方法的探討及精度的分析。
1 三角高程測量原理
三角高程測量是根據(jù)觀測兩點之間的高度角及斜距來計算兩點間高差的,兩點間高差為:

其中,s為兩點間斜距;a為垂直角;k為大氣垂直折光系數(shù);i為測站點儀器高;v為觀測目標(biāo)高;R為地球曲率半徑。
由式(1)可以看出,三角高程測量兩點高差的精度受到兩點間斜距的量取精度、兩點間豎直角的觀測精度、大氣折光、儀器高及棱鏡高量取精度的影響[1]。在這些因素的影響下,普通三角高程精度較差,很難滿足沉降觀測的精度要求。
2 單棱鏡中點法
單棱鏡中點法就是將全站儀架設(shè)在基準(zhǔn)點和觀測點中間,分別測出基準(zhǔn)點到全站儀的高差和觀測點到全站儀的高差,再計算出基準(zhǔn)點和觀測點之間的高差,進(jìn)而得到觀測點的高程。
兩點間的高差計算公式為:

由式(2)可以看出,兩點間高差誤差主要與斜距s,豎直角a,大氣折光系數(shù)k及棱鏡高v有關(guān)。而不需要量取儀器高,如果在基準(zhǔn)點和觀測點用相同的一支對中桿且不變換高度,即v1=v2。但是對于環(huán)境復(fù)雜的施工現(xiàn)場,觀測點不便于架設(shè)棱鏡,可在觀測點設(shè)置反光貼片,使v2=0。基準(zhǔn)點棱鏡高獲取,可先測出基準(zhǔn)點與全站儀之間的水平距離D1,用全站儀照準(zhǔn)基準(zhǔn)點上的棱鏡中心,使全站儀望遠(yuǎn)鏡水平、豎直制動,測得豎直角為a1,移走棱鏡對中桿,在基準(zhǔn)點放置水準(zhǔn)尺,讀數(shù)為a,旋轉(zhuǎn)豎直微動螺旋,使全站儀十字絲的橫絲對準(zhǔn)最靠近讀數(shù)a的整數(shù)刻畫b,此時,豎直角為a3。
則棱鏡高的精確值為:
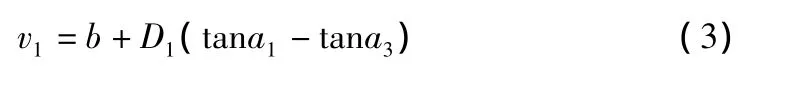
3 誤差分析
根據(jù)誤差傳播定律,單棱鏡中點法高差中誤差公式為:
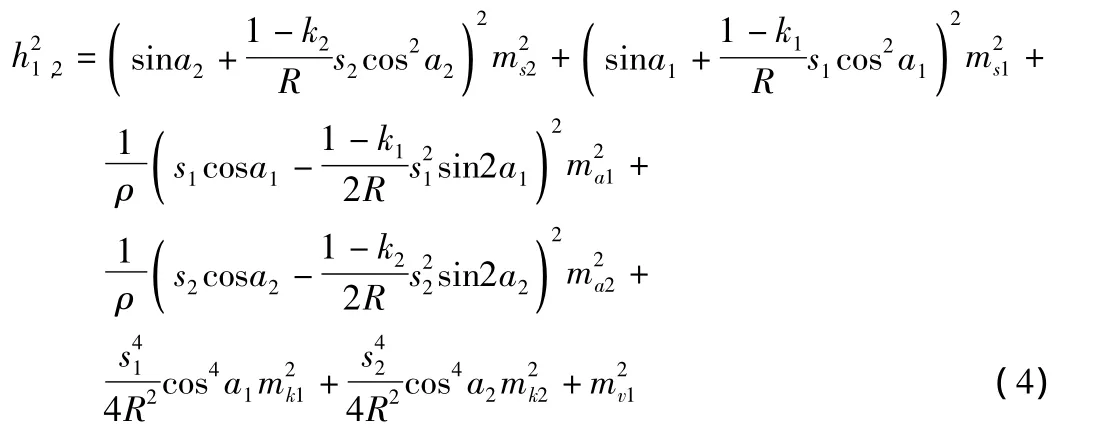
在相同環(huán)境下的一定范圍內(nèi),同類型觀測精度相同,短時間內(nèi)對前后目標(biāo)進(jìn)行觀測,大氣折光對精度影響較小,故式(4)可寫成:

由式(4),式(5)分析可知,影響精度的主要因素為測角、測距中誤差及棱鏡高量取中誤差。主要取決于全站儀的精度及測量方法。采用天寶S8全站儀,測角精度±0.5″、測距精度為±(1 mm+1×10-6D),不同的角度和距離得到不同的測站高差中誤差,見表1。

表1 角度、視距與測站高差中誤差 mm
根據(jù)《建筑變形測量規(guī)范》中建筑變形測量級別與精度指標(biāo)要求,沉降觀測觀測點測站高差中誤差:特級≤0.05 mm,一級≤0.15 mm,二級≤0.50 mm,三級≤1.50 mm。由表1可以看出高差中誤差隨著豎直角和視距的增加而變大,當(dāng)豎直角小于15°視距小于70 m或豎直角小于10°視距小于90 m,沉降監(jiān)測測量精度可達(dá)到建筑變形測量等級二級精度要求;在豎直角不大于3°視距不大于20 m時,甚至可達(dá)到建筑變形測量等級一級精度要求。
4 實驗驗證與分析
為了驗證上述方法實施沉降監(jiān)測的可行性,某在建建筑物上設(shè)置了4個觀測點進(jìn)行試驗。首先,利用精密水準(zhǔn)測量方法精確獲取基準(zhǔn)點與觀測點之間的高差。然后,在觀測點上設(shè)置反光片,利用文章方法用天寶S8全站儀觀測,并計算觀測點高程及兩種方法所得高程較差,結(jié)果如表2所示。

表2 不同方法的高程比較 mm
由表2可以得出,4個觀測點的三角高程與精密水準(zhǔn)高程較差最大為0.40 mm,滿足《建筑變形測量規(guī)范》中規(guī)定沉降觀測觀測點測站高差中誤差不大于0.50 mm的建筑變形測量等級二級要求,這說明中間設(shè)站式三角高程實施沉降監(jiān)測的方法是完全可行的。
5 結(jié)語
本文通過分析精密三角高程測量原理與誤差來源,提出中間設(shè)站式三角高程實施沉降監(jiān)測方法,分析證實了該方法的可行性。該方法有效地消除了影響精度的各類誤差,可以方便快捷地獲取監(jiān)測體的沉降數(shù)據(jù),測量精度能夠滿足了建筑變形測量二級精度要求,減小了工作強度,提高了工作效率。
[1]晏紅波,黃 藤,鄧 標(biāo).智能全站儀精密三角高程測量替代二等水準(zhǔn)測量[J].水電自動化與大壩監(jiān)測,2007,31(4):43-44.
[2]張正祿,吳棟才.精密工程測量[M].北京:測繪出版社,1993.
[3]張自立.全站儀三角高程測量替代三、四等水準(zhǔn)測量[J].城市建設(shè)與理論研究,2011(10):259-263.
[4]張正祿.精密三角高程代替一等水準(zhǔn)測量的研究[J].武漢大學(xué)學(xué)報(信息科學(xué)版),2010,30(7):2-5.
[5]周斌武.應(yīng)用全站儀進(jìn)行三角高程測量的新方法[J].甘肅農(nóng)業(yè),2005(11):33-34.
[6]郭春喜.精密三角高程替代二等水準(zhǔn)的可行性研究[J].測繪信息與工程,2010(2):42-43.
[7]周國樹,郭 清.微視距精密三角水準(zhǔn)研究[J].測繪通報,2006(4):6-9.
[8]莫南明,過靜珺,張勝良,等.CCTV主樓施工變形監(jiān)測技術(shù)應(yīng)用研究[J].測繪工程,2007(5):48-52.
[9]鄧清軍,高 飛,李曉莉.利用自由設(shè)站法進(jìn)行數(shù)字化測圖的探討[J].合肥工業(yè)大學(xué)學(xué)報(自然科學(xué)版),2009,32(7):9-11.
[10]曾鼎華,張永興.三角形量測法在隧道變形監(jiān)測中的應(yīng)用研究[J].水文地質(zhì)工程地質(zhì),2005(5):113-115.

