基于一元線性回歸的變形監測數據處理與分析
苗元欣
(山東省地質礦產勘查開發局第五地質大隊,山東泰安 271000)
1 工程概況
濟寧體育東片區工程4號樓是其中的一個商住樓工程,根據工程進展情況,為了避免施工期間建筑物發生不均勻沉降而造成建筑物的傾斜或倒塌,進而導致人身安全和經濟財產損失,于是對該商住樓工程進行了沉降觀測。依據監測方案,在該樓上共布設了8個監測點,從2012年12月5日~2013年4月6日,進行了11次的觀測。本文中依據實際采集的數據,運用回歸分析對該樓的變形監測數據進行了處理與分析。
2 一元線性回歸分析的數學模型
一元線性回歸模型是針對一個自變量和一個因變量之間的近似線性關系,用一元線性方程去擬合,進而用得到的線性方程去預測。一元線性回歸預測是最基本、最簡單的回歸預測方法,也是學習其他回歸預測方法的基礎。
一元線性回歸的數學模型為:

其中,y為預測對象,稱為因變量;x為影響因素,稱為自變量;a,b均為待定的回歸系數;ε為隨機誤差。
3 數據處理流程
對于多期建筑變形觀測成果,根據需要建立描述變形量與變形因子間關系的數學模型,對引起變形的原因作出分析和解釋,必要時還對變形的發展趨勢進行預報。
當一個變形體上所有觀測點或部分觀測點的變形狀況總體一致時,可利用這些觀測點的平均變形量建立相應的數學模型。當各觀測點變形狀況差異大或某些觀測點變形狀況特殊時,應對各觀測點或特殊的觀測點分別建立數學模型。
3.1 數據分析
通過對每期水準測量得到的數據結果平差處理后,得到各個監測點的高程值,據此可以計算出各個監測點的累積沉降量,根據建筑物各點的累積沉降量繪制建筑物累積沉降量曲線圖(如圖1所示)。

圖1 建筑物累積沉降量曲線圖
由圖1可知,各點的累積沉降量相差不大,且沉降速率大致相同,可見地基處理是可靠有效的。沉降曲線速率先逐漸增加,沉降速率變快,之后沉降速率又有所減慢,以后的曲線并沒有出現異常值和中斷現象,表明工作基點和觀測點比較穩定,沒有發生太大的沉降,大樓在施工階段的下沉平穩,其沉降速率滿足規范要求。
3.2 數據建模
本文以各監測點前8次累積沉降量為因變量,建筑物的觀測累積時間為自變量進行回歸分析,設建筑物累積時間為自變量x,累積沉降量為因變量,假設它們之間存在著線性關系,利用 excel建立各點的回歸方程。現以4.1號點為例來進行說明。
根據4.1號點累積沉降量和累積時間數據,繪制散點圖,大體呈線性相關,添加線性回歸分析,得到圖2和回歸方程。

圖2 4.1號點累積沉降量和時間關系圖
3.3 線性顯著性的檢驗
為了保證所求得的回歸方程的可靠性,需要對每個方程進行其線性顯著性檢驗。以4.1號點為例,其線性檢驗計算表見表1,計算過程如下。

表1 4.1號點線性檢驗計算表
由式(2)~式(4):
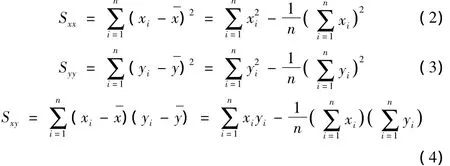
得:Sxx=13 708.545 45,Syy=508.687 272 7,Sxy=2 588.481 818。
又由式(5):
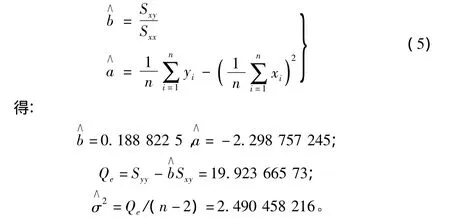
在以上的討論中,假定y關于x的回歸具有形式a+bx,若假設符合實際,則b不應為0,若b=0,則回歸效果是不顯著的。因此假設:

當H0為真時,b=0,此時:且,即得H0的拒絕域為:
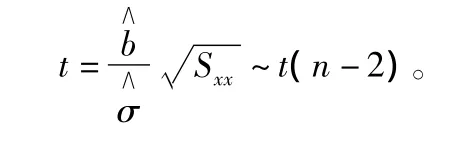
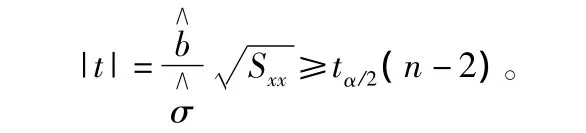
其中,α為顯著性水平。
代入數據得 t=14.009 085 98。取 α =0.05,查表得 tα/2(n -2)=2.262 2,故成立,即拒絕域 H0:b= 0,認為回歸效果是顯著的。
4 沉降預報
以各監測點的前8次累積變化量,以及樓房層數的變化,通過一元線性回歸分析可以預測出后幾次的累積變化量,表2是預測的累積變化量值和實際累積沉降量比較,圖3是其相應的圖形表示。

表2 4.1號點第 9,10,11 期數據的預測累積沉降量和實際累積沉降量比較
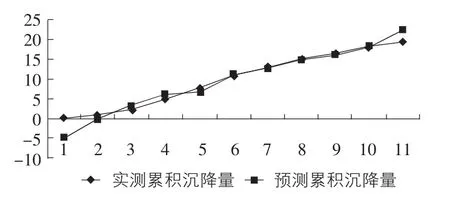
圖3 4.1號點實測值與預測值比較圖
5 結語
從圖3可以看出,4.1號點的預測結果與實際觀測值相比較誤差均相對較小,只是首次和最后一次相差較大。這是因為:預測模型是線性模型,如果建筑物發生的沉降呈現出完全的線性形態,則預測值將會比較準確。而該點在該期的監測數據與前幾期相比較發生了不均勻的沉降,所以預測值與實測值之間誤差較大;最后一次觀測,各監測點的預測結果與實際觀測值相比較誤差均相對較大,是因為此時樓房已封頂,荷載增加后,樓房整體的沉降量較大。同理,可以對其他的點進行以上的分析,分析的結果表明,體育東片區4號樓的變形量較小,總體是穩定的。
[1]梅長林,王 寧.近代回歸分析方法[M].北京:科學出版社,2012.
[2]Samprit Chatterjee,Ali S.Hadi,Bertram Price.Regression Anslysis by Example(翻譯版)[M].the third edition.北京:中國統計出版社,2004.
[3]于 濤,趙仲榮.建筑物沉降規律的曲線擬合模型研究[J].測繪通報,2008(11):50-52.
[4]陳偉清.回歸分析在建筑物沉降變形分析中的應用[J].廣西城鎮建設,2005(3):35-38.
[5]韓 正,杜海霞,龍 飛,等.高層建筑沉降觀測及其數據分析[J].城市勘測,2009(1):108-110.
[6]盛 驟,謝式千,潘承毅.概率論與數理統計[D].杭州:浙江大學,2008:244-257.
[7]楊若霖,張思恒.基于回歸分析的測量數據處理方法[J].科技信息,2012(35):114-115.

