基于主成分分析法的渭河陜西段水環境質量評價

吳 勇，劉有軍，陳 偉，江 強

(云南省建筑科學研究院，云南昆明650223)

水環境質量評價就是通過一定的數理方法和其他手段，對水環境素質的優劣進行定量描述的過程。水環境質量評價必須以監測資料為基礎，經過數理統計得出統計量 (特征數值)及環境的各種代表值，然后依據水環境質量評價方法及水環境質量分級分類標準進行環境質量評價。然而水環境系統是一個復雜的系統，在分析過程中，需要對多個變量進行分析，由于變量個數眾多且彼此之間存在著一定的相關性，使得對主要信息的提取變得十分復雜。僅僅靠單一的指標來評價水環境質量的污染程度，難免產生片面性。因此對水環境質量進行綜合評價的最大難點就是多目標性，即需要考慮眾多表征水環境質量的指標。如何科學地、客觀地將一個多指標問題綜合成為少數幾個指標問題成為水環境質量評價的研究重點。

近年來，隨著多元統計分析的普及和應用，主成分分析法也成為一種新興的評價方法，在環境質量綜合評價方面應用廣泛。主成分分析法能將高維空間的問題轉化到低維空間去處理，使問題變得比較簡單、直觀，而且這些較少的綜合指標之間互不相關，又能提供原有指標的絕大部分信息［1］。而且，伴隨主成分分析的過程，將會自動生成各主成分的權重，這就在很大程度上抵制了在評價過程中人為因素的干擾。

1 環境現狀

渭河在“品字泉”源頭，其水質良好，清澈透亮，沁人心脾。從源頭往下，進人水土流失區，河水由清變濁、由濁變渾。據有關資料介紹，在定西境內，河水含沙量達66.4kg/m3。渭河甘肅段有污染源87家，其中工業污染源62家，年接納工業廢水和生活污水2622萬t。根據甘、陜環境保護部門的監測資料，渭河至陜西鳳閣嶺后，除個別指標超標外，其水質多年來均符合《地面水環境質量標準》Ⅲ類水標準，可以滿足工農業用水的要求。

渭河陜西段有工業企業8000多家，呈串珠式分布于渭河及其支流兩岸;尚有50多萬個鄉鎮企業，其中鄉鎮工業企業達15萬個左右。據對縣及縣以上工業企業的環境統計，渭河年接納工業廢水3.2億t，城市生活污水1.69億t;工業廢水、生活污水處理率分別為77.9%、21%左右，絕大多數生活污水和22%的工業廢水未經處理直接排入渭河水系。渭河水系年接納重金屬4.46t、有機污染物約10.75萬t，其中COD達10.66萬 t，約占有機污染物的99.2%。由于含重金屬的工業廢水已在20世紀80代基本治理達標，向渭河排放的重金屬的數量較少，而渭河又是一條多泥沙、河槽寬闊、比降較小的河流，水流速度較慢、水層亦較淺，易于泥沙對重金屬離子的吸附和沉降，河水中重金屬的濃度較低，只有個別斷面某種金屬離子濃度超過地面水的Ⅲ類水的標準。渭河流經寶雞、咸陽、西安和渭南等市，受到有機污染物的重復污染，已超出其稀釋和自凈能力，呈有機型污染特征，以氨氮、高錳酸鹽指數、生化需氧量和揮發酚污染較為突出。

2 主成分分析法

2.1 方法簡介

主成分分析法 (prineipalcoplllonentarialysis，PCA)也許是多變量分析中最古老和最著名的技術。最早是由美國統計學家皮爾遜 (PEARsoN)在1901年的生物學理論研究中引入的。是從多指標分析出發，運用統計分析原理與方法提取少數幾個彼此不相關的綜合性指標而保持其原指標所提供的大量信息的一種統計方法。1933年，HOTELLING［2］將此想法應用于心理學研究，并得到了進一步的發展。1947年，KARHuNEN［3］獨立地用概率論的形式再次將其研究，其后LOEVE將該理論進一步擴充和完善，故PCA理論也稱為KAHRUNENLOEVE變換。

2.2 基本原理

主成分分析法的工作對象是樣本點x定量變量類型的數據表。它的工作目標，就是要對這種多變量的平面數據表進行最佳綜合簡化。也就是說，要在力保數據信息丟失最少的原則下，對高維變量進行降維處理［4］。

除了降低多變量數據系統的維度以外，主成分分析同時還簡化了變量系統的統計數字特征。對于任意p個變量，描述它們自身及相互關系的數字特征包括均值、方差、協方差等，一共有P+(1/2)p(P+l)個參數。經過主成分分析后，每個新變量系統的數字特征減少了P+(1/2)p(p－1)個。假定有n個水體樣本，每個樣本共有p個指標變量，則構成了一個n×p階的地理數據矩陣

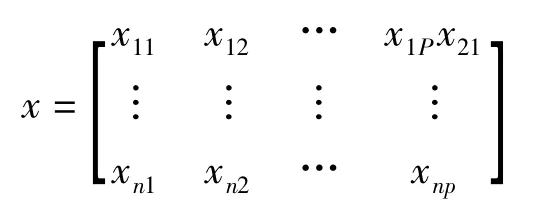
利用p個原始變量構成少量幾個新的綜合變量，使得新變量為原始變量的線性組合，記原來的變量指標為x1，x2，…，xP，z1，z2，…，zm(m≤p)為新變量指標，則:

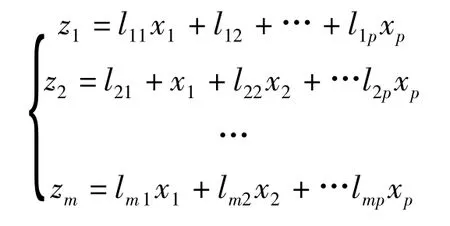
z1，z2，…，zm分別稱為原變量指標 x1，x2，…，xP的第一，第二，…，第m主成分，在實際問題的分析中，常挑選前幾個最大的主成分。①zi與zj(i≠j;i，j=1，2，…，m)相互無關;②z1是x1，x2，…，xP的一切線性組合中方差最大者，z2是與z1不相關的x1，x2，…，xP的所有線性組合中方差最大者;……;zm是與 z1，z2，……，zm－1都不相關的x1，x2，…，xP的所有線性組合中方差最大者。

3 數據的收集、處理及分析

3.1 MATLAB數據處理軟件

MTLAB是美國Math Works公司出品的商業數學軟件，用于算法開發、數據可視化、數據分析以及數值計算的高級技術計算語言和交互式環境，主要包括MATLAB和Simulink兩大部分。本次采用MATLAB數據處理軟件主要是進行高級矩陣和陣列語言的計算。

3.2 數據收集

本次對渭河干流陜西段共選取了8個斷面，分別為咸陽鐵橋S1、草灘橋S2、耿鎮橋S3、新豐橋S4、黑河入渭S5、澇河入渭S6、新河入渭S7、臨河入渭S8共8個斷面進行檢測，評價選用溶解氧、生化需氧量、高錳指數、氨氮、揮發酚、氰化物、汞、六價鉻8個評價參數，表1為檢測數據。

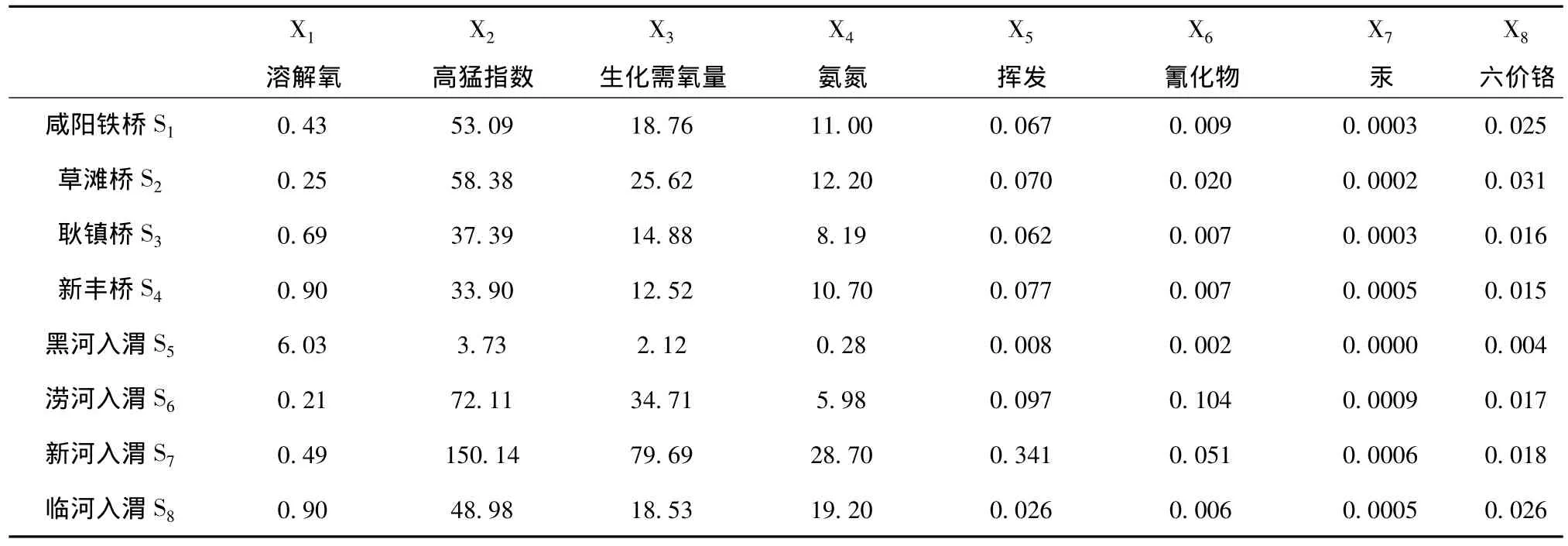
表1 渭河8個斷面檢測結果表

表2 檢測數據標準化處理后的結果

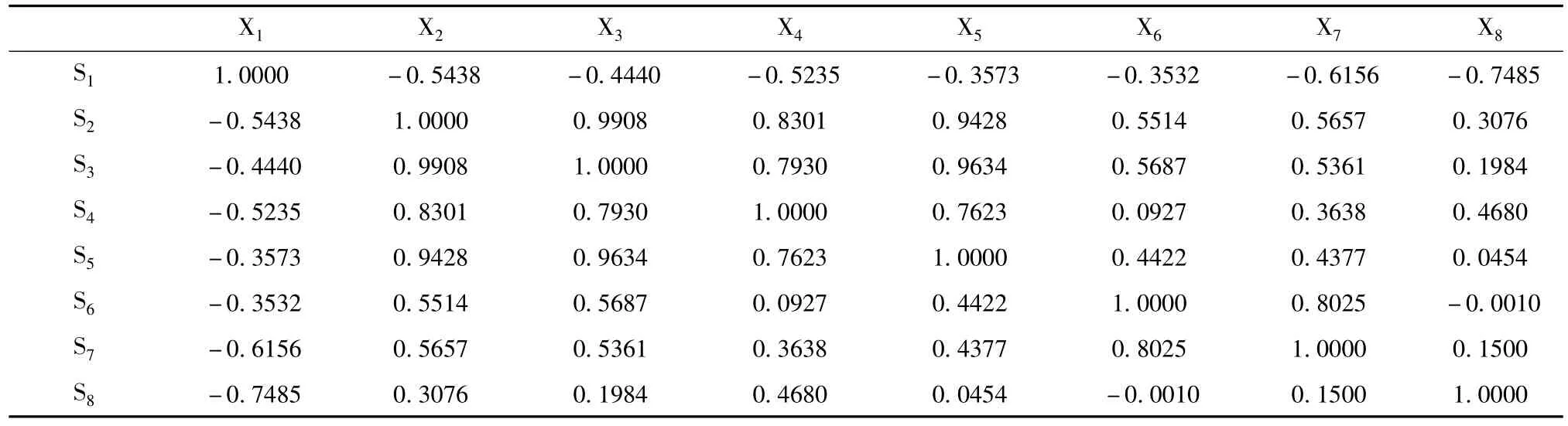
表3 檢測指標相關系數矩陣

3.3 數據計算及結果

對同一變量減去其均值再除以標準差得到的新數據為標準化后的數據。對于特殊評價參數溶解氧，首先對其進行導數處理，然后再進行標準化處理，表2為檢測結果標準化后的數據。根據標準化數據計算相關數矩陣，檢測指標相關系數矩陣如表3所示。

再由相關系數矩陣計算特征值，以及各個主成分的貢獻率與累計貢獻率，特征值、特征向量的計算是根據MATLAB軟件結合計算而來。計算數據見表4、5、6，由此可知，第一，第二，第三主成分的累計貢獻率已高達86.5%，故只需求出第一、第二、第三主成分z1，z2，z3即可。

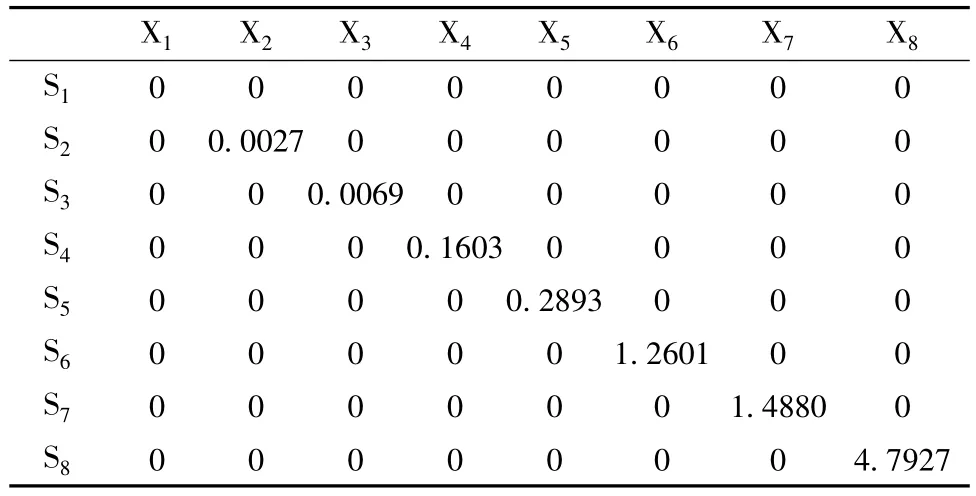
表4 特征值

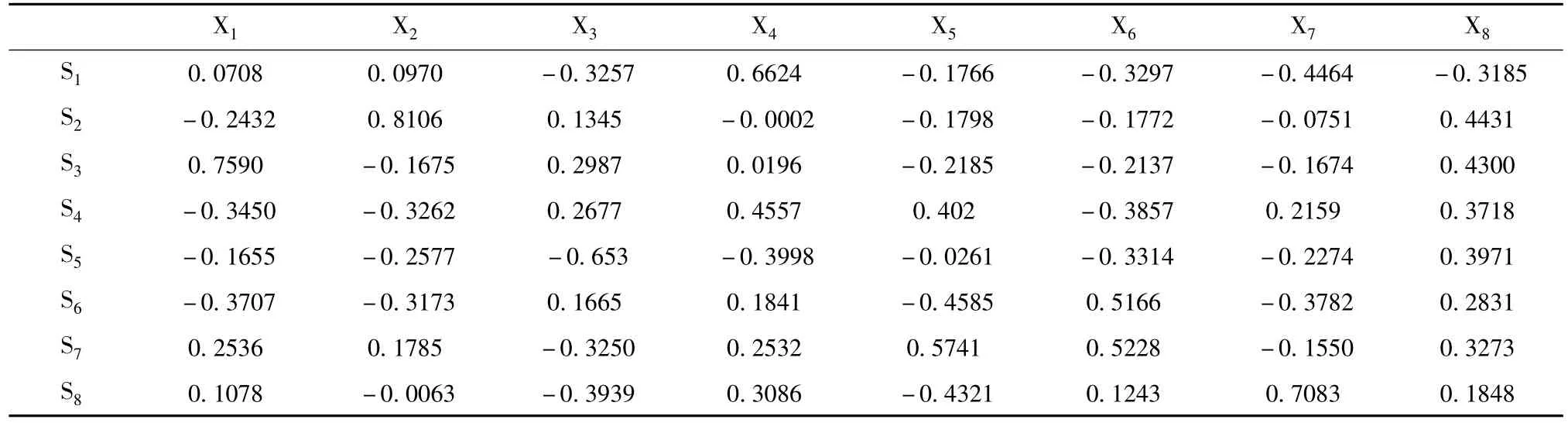
表5 特征向量表格

表6 特征值和累計貢獻率

根據主成分載荷公式計算主成分載荷，根據特征值 λ1=4.7927，λ2=1.4880，λ3=1.2601分別求出其特征向量e1，e2，e3，再用公式(i，j=1，2，3，…，p)，計算各變量在主成分1，2，3上的載荷。

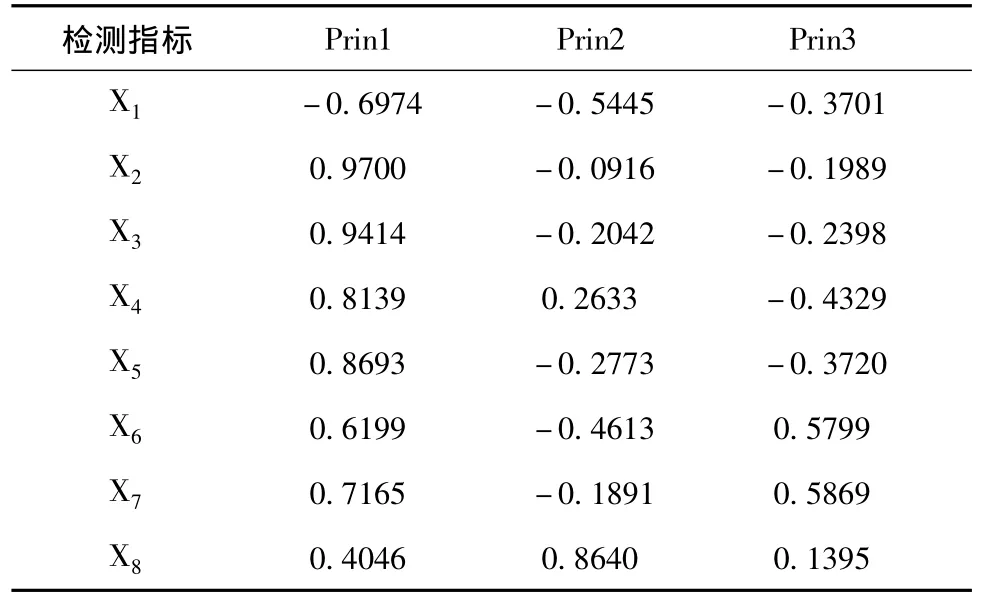
表7 檢測指標載荷矩陣

從表3的相關矩陣出發，計算各主成分的特征值、方差貢獻率及累積方差貢獻率和各監測指標的載荷矩陣，結果見表6和表7。由表7中相關系數陣的特征值可以看出，前3個主成分已滿足≥85%的條件，因此只需用3個主成分取代原有8個指標，就能很好地表達。由表7監測指標的載荷矩陣計算前3個主成分的表達方式:

將各監測斷面的標準化數據代入所提取的3個主成分公式中，得到各斷面的主成分，再根據Prin1、Prin2、Prin3和對應的客觀權重 e1、e2、e3(方差貢獻率)的積之和計算得出各監測斷面的綜合主成分Prin1～3，監測斷面的主成分計算結果如表8所示。根據《地面水環境質量標準》(GB3838－2002)，和《地表水資源質量標準》(SL63－94)可得水質分級標準，如表9所示。

根據表8的各個監測斷面綜合主成分，參考綜合主成分分級標準表8得到各個斷面的水質類別:黑河入渭 (S5)水質屬于Ⅰ類;耿鎮橋 (S3)水質屬于Ⅲ類;咸陽鐵橋 (S1)、新豐橋 (S4)水質屬于Ⅳ類;草灘橋 (S2)、澇河入渭 (S6)、新河入渭 (S7)以及臨河入渭 (S8)水質屬于Ⅴ類。由此可見，黑河入渭 (S5)水質最好，其他斷面的水質均受到不同程度的污染，渭河陜西段水體綜合水質為Ⅴ類，污染很嚴重，不能滿足此區域河流水體的功能要求。

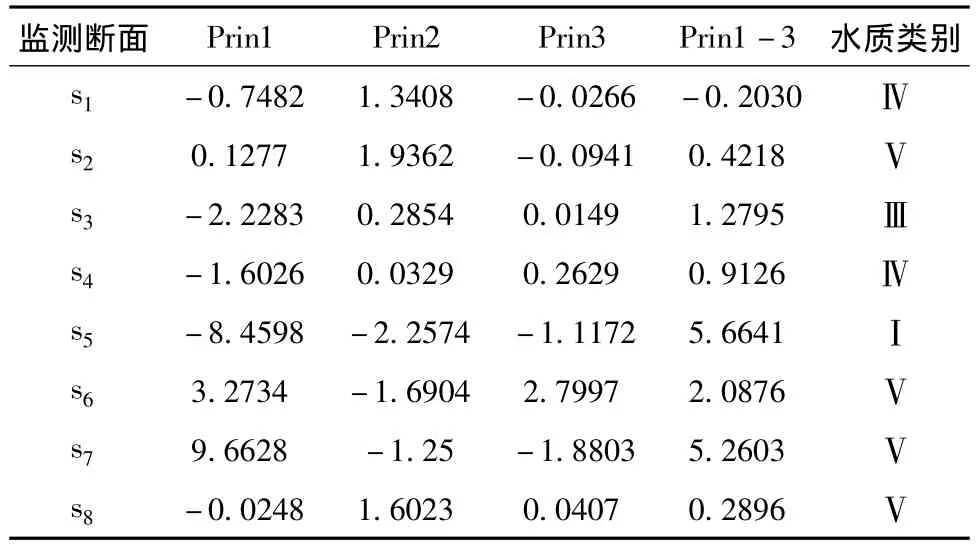
表8 各監測斷面的主成分

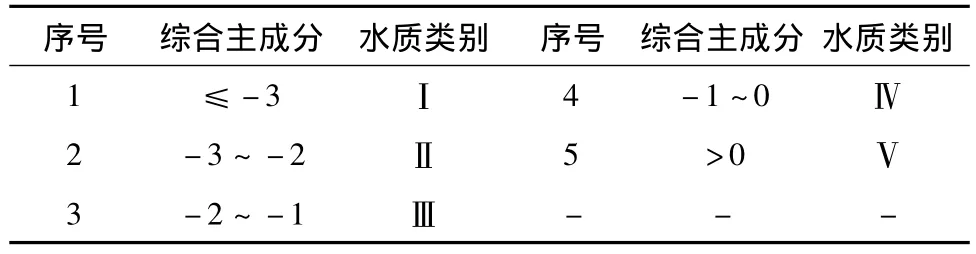
表9 水質分級標準

3.4 結果原因分析

(1)造紙企業數量多、規模小、分布廣。2007年不完全統計全省共有造紙企業850多家，平均規模為400 t/a，可見CODMn污染指數較高主要是造紙企業引起的。

(2)化肥和農藥使用不合理。寶雞市土壤養分失衡問題一直比較突出，由于大量使用廉價劣質的氮肥和農藥，以及氮、磷、鉀肥施用不成比例，因此使氮肥溶解而被沖入水體中造成污染。

(3)河道生態水量不足。渭河寶雞峽林家村引渭工程近310年年平均取水量為4.83億m3，占河道水量的49.07%，造成河道生態水量大幅下降、水體污染物濃度得不到稀釋，這也是現今污染指數居高不下的重要原因。

4 結論

(1)主成分分析法具有較好的精確度，其可以通過細化的計算數值反應，能有效地用于水環境質量評價中;MATLAB數據處理軟件是現今運用較廣泛的數據處理系統。

(2)渭河陜西段水體綜合水質為Ⅴ類，污染很嚴重，不能滿足此區域河流水體的功能要求。

(3)渭河陜西段水的污染主要是由造紙企業污水排放、化肥和農藥使用不合理及河道生態水量不足引起的。

［1］王曉鵬.河流水質綜合評價之主成分分析法［J］.數理統計與管理，2001，20(4):49－52.

［2］HotellingH.Analysis of a eomplex of statistieal variables into prineipal component［J］.Journal of Edueational Psyehology，1933，(24):417－441，498－520.

［3］KarhunenK.Uber 1ineare methoden in der washrseheinliehkeitsreehnung ［J］.AnIer Aeard Sei，Fennieade Ser A l，1947，37:3 －79.

［4］任若恩，王惠文.多元統計數據與分析——理論、方法、實例［M］.北京:國防工業出版社，1999.