混凝土箱梁考慮翼板厚度變化的剪力滯效應

藺鵬臻，楊子江，劉鳳奎，冀 偉，張元海

（蘭州交通大學a.甘肅省道路橋梁與地下工程重點實驗室；b.土木工程學院，蘭州 730070）

混凝土箱梁是目前橋梁結構采用較為廣泛的梁體結構形式。考慮到截面受力、構造和施工因素，箱梁頂、底板和懸臂板均為沿截面寬度方向變厚度，通常越靠近腹板越厚，而頂、底板中部和懸臂端部越薄［1－2］。由于箱梁總體上仍然存在薄壁結構的特點，其剪力滯效應必然會由于翼板厚度的橫向變化而區別于既有研究中考慮的等厚度情況，因此，開展針對混凝土箱梁翼板厚度變化對剪力滯效應影響的研究具有理論和實踐意義。

對箱梁剪力滯效應的研究方法，較為通用的包括變分法和三維板殼或塊體有限元法等［1，5－6］。變分法由于力學推理明晰、計算結果與普通梁理論能較好對應而廣受歡迎。但變分法分析箱梁均以翼板等厚度箱梁為對象［1，3－7］，而對于常見的翼板變厚度的混凝土箱梁，則主要通過三維板殼或塊體有限元數值仿真方法研究其剪力滯效應［8］。由于板殼和塊體有限元分析結果數據量大、且主要以單元或結點的應力和應變解為結果，不能與現有以梁理論為基礎設計規范有機結合，故分析結果也主要用于宏觀掌握結構的受力規律。

針對翼板沿截面寬度方向變厚度的混凝土箱梁，筆者利用勢能變分原理，建立了單室混凝土箱梁的剪滯效應分析方法，針對常見的簡支梁和懸臂梁結構，重點研究了翼板厚度變化對箱梁應力和變形的影響規律。

1 基于變分法的剪滯控制微分方程

對于圖1所示的混凝土薄壁箱梁，在豎向荷載作用下，截面的彎曲變形將伴隨著截面面外的翹曲而產生剪力滯后效應，從而在橫截面上存在著服從平截面假設的剪滯翹曲位移。如定義w（x）為橫截面任一點 （x，y，z）的豎向撓曲位移，w′（x）為相應的轉角，u（x，y，z）為縱向位移，f（y，z）為截面的剪力滯翹曲位移函數，u（x）為截面廣義剪滯翹曲位移。正方向為：線位移以圖1坐標方向為正，轉角以順時針方向為正。橫截面的縱向位移可表示為：

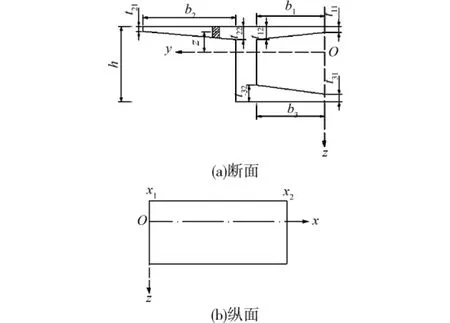
圖1 混凝土箱梁及坐標系

有了截面任一點的縱向位移表達式，則相應可得到截面的正應變和剪應變：

梁體的應變能可表示為對于梁段體積V的積分：

設梁段外力引起的彎矩為M（x），則梁體的外力勢能為［1］：

將式（2）帶入式（3）并對每一塊翼板進行體積積分。在此過程中定義如下廣義截面常數［9］：

全截面豎向彎曲慣性矩I：

全部翼板的剪滯翹曲慣性矩Iu：

全部翼板的剪滯翹曲慣性積Iyu：

全部翼板的剪滯翹曲面積Au：

則梁段的總勢能可表示為：

根據最小勢能原理，并結合變分方法［10］，可得到基于變分原理的控制微分方程：

式（10）就是混凝土箱梁基于變分原理的基本微分方程，其中前2式為控制微分方程，第3式為變分所要求的縱向剪力滯位移函數的自然邊界條件。將式（10）中第1式求一階導數，并和第2式合并整理，可得到剪力滯翹曲位移u、考慮剪力滯效應的梁體彎曲曲率w″以及截面應力σ的表達式［11］：

2 翼板翹曲位移函數及廣義截面特效計算

由式（12）和（13）可以看出，影響結構剪力滯效應的主要參數為廣義截面常數I、Iyu、n和k，以及翹曲形函數f（y，z），而求Iyu、n和k首先需確定翹曲形函數。

為單室混凝土箱梁定義筆者提出的基于翼板剪切變形規律的剪力滯翹曲位移函數［11］：

式中A1、A2分別為內側頂板和懸臂板的面積，As、Ax分別為頂板（內側頂板和懸臂板）和底板的面積，Zs和Zx分別為截面中性軸距離上下翼板中面的距離。

結合混凝土箱梁截面幾何特征，可利用式（14）和式（5）～（8）獲得其廣義截面常數的計算表達式。

3 翼板厚度變化對剪力滯效應的影響

1）算例參數 以文獻［4］的翼板等厚度有機玻璃模型為原型，改變翼板沿截面寬度方向的厚度，使其具有常規混凝土箱梁的翼板變厚度特點。進行翼板厚度進行等面積原則下的厚度變化：翼板（頂板、底板和懸臂板）平均厚度t0為6mm不做變化，從而保證翼板面積的不變，截面整體的抗彎慣性矩I也基本不變，以此消除截面抗彎剛度的影響。增大腹板部位翼板厚度至t2，減小懸臂端和箱梁中心部位翼板厚度至t1。定義翼板厚度比β為t2和t1的比值。改變翼板厚度比分別為1.0、1.3、1.7、2.5和5，如圖2所示。模型跨徑為800mm，平均彈性模量為E＝3000MPa，波泊松比為μ＝0.385。

圖2 算例箱梁（mm）

2）分析結構 選擇橋梁結構最常見的基本體系簡支梁和懸臂梁。簡支梁分別作用272.2N的跨中集中力和滿跨1N／mm均布荷載。懸臂梁分別作用272.2N的梁端集中力和滿跨1N／mm均布荷載。

3）正剪力滯效應 理論分析表明［1］，簡支梁在跨中集中力和滿跨均布荷載下的全跨、懸臂梁在梁端集中力和滿跨均布荷載下的懸臂根部等彎曲正應力最大部位均為正剪力滯效應區域。為了分析考慮厚度變化對剪力滯效應的計算精度影響，定義變厚度影響率ρ：

可以通過變厚度影響率ρ反映變厚度翼板按照等厚度計算時的誤差大小，也可以反映出不同翼板厚度變化幅度（β反映）對計算結果的影響。本算例各β取值下的ρ值計算結果如圖3所示。

圖3 正剪力滯效應的影響

由圖3可以看出，隨著翼板厚度比β的增大，截面控制點應力的厚度影響率ρ均增大，但是影響率增大趨勢不同。對1和3點考慮翼板厚度變化時，應力比不考慮翼板厚度變化的要大，且厚度比越大應力值越大；對2和4點考慮翼板厚度變化時，應力比不考慮翼板厚度變化的要小，且厚度比越大應力值越小。總體可以看出，考慮變厚度的計算方法比不考慮變厚度而采用等厚度簡化計算的誤差最大可達到15%，因此對混凝土箱梁進行考慮翼板變厚度的分析是非常必要的。

4）負剪力滯效應 既有研究表明，懸臂梁在承受均布荷載時，剪力滯效應在梁端至根部的一定區域內將由負變為正。對于處在負剪力滯效應區段的跨中部位，各β取值下的ρ值計算結果如圖4所示。

圖4 負剪力滯效應的影響

從圖4可以看出，負剪力滯區域翼板應力厚度影響率的變化規律與正剪力滯截面相同，也是隨著β增大ρ增大。

5）剪力滯彎曲變形 箱梁的撓度通常包括初等梁撓度、剪力滯和剪切變形引起的附加撓度3部分［1］。初等梁撓度主要與截面的抗彎慣矩I有關，剪切變形撓度主要與截面腹板的剪切面積有關。當改變翼板厚度時，結構撓度的改變主要由于剪力滯計算參數的變化引起。以本算例的簡支梁和懸臂梁，可求得翼板厚度改變后，簡支梁跨中、懸臂梁梁端的剪力滯撓度。

定義fF為剪力滯撓度，f0為按照初等梁理論計算的撓度，則

δ＝fF／f0×100%

反映剪力滯撓度與初等撓度的百分比。

改變翼板厚度后，簡支梁和懸臂梁的最大撓度部位的剪力滯撓度變化如圖5所示。

可以看出，隨著翼板厚度比的增大，由剪力滯效應引起的梁體附加撓度減小。因此可以認為，增大翼板厚度比，減小了由于剪力滯效應對結構整體剛度的削弱，從而使得結構整體剛度增大，撓度減小。和懸臂梁相比，簡支梁結構翼板厚度變化對梁體撓度的影響較大。

圖5 剪力滯變形的影響

4 結 論

1）對翼板沿截面橫向變厚度的混凝土箱梁，通過定義截面廣義截面特性，可建立反映翼板厚度變化影響的剪力滯應力和變形的解析解答。

2）理論分析表明，在翼板等面積原則下，隨著翼板厚度比的增大，截面控制點應力的厚度影響率均增大，并且總體趨勢是：靠近腹板部位的翼板應力（2和4點）比不考慮翼板厚度變化的計算結果要小，靠近箱梁截面中心的翼板應力（1和3點）比不考慮翼板厚度變化的計算結果要大。

3）由控制點的位置和應力綜合評判，對箱梁截面設計而言，增大翼板厚度比，可使得截面剪力滯效應趨于平緩。綜合算例得出，對翼板橫向變厚度的混凝土箱梁，考慮變厚度的計算方法比不考慮變厚度而采用等厚度簡化計算的誤差最大可達到15%，因此對混凝土箱梁計算考慮翼板變厚度的影響是非常必要的。

4）對剪力滯剛度的分析表明，考慮翼板厚度變化總體上減小了截面的剪力滯撓度，反映出翼板厚度變化對剪力滯效應具有平抑作用。

［1］郭金瓊，房貞政，鄭振.箱形梁設計理論［M］.2版.北京：人民交通出版社，2008.

［2］鄭健.中國高速鐵路橋梁［M］.北京：高等教育出版社，2008.

［3］周世軍.箱梁的剪力滯效應分析［J］.工程力學，2008，25（2）：204－208.Zhou S J.Shear lag analysis of box girders［J］.Engineering Mechanics，2008，25（2）：204－208.

［4］羅旗幟.薄壁箱形梁剪力滯計算的梁段有限元法［J］.湖南大學學報，1991，18（2）：33－38，55.Luo Q Z.Calculation of shear lag in thin walled box girders by the finite segment method ［J］.Journal of Hunan University，1991，18（2）：33－38.

［5］Reissner E.Analysis of shear lag in box beams by the principle of minimum potential energy［J］.Quarterly of Applied Mathematics，1946（4）：268－278.

［6］Dezi L.Mentrasti.nonuniform bending－stress distribution（shear lag）［J］.Journal of Structural Engineering，1985，111（12）：2675－2689.

［7］曹國輝，方志.變分原理分析連續箱梁開裂后的剪力滯效應［J］.工程力學，2007，24（04）：75－80.Cao G H，Fang Z.Shear lag effect of cracked continuouse box girder analyzed by variational principle［J］.Engineering Mechanics，2007，24（4）：75－80.

［8］Manoj K，Sagar S.Influence of box shape on structural behaviour of RC box girder bridges［J］.Indian Concrete Journal，2007，81（6）：55－62.

［9］張元海，李喬.箱形梁剪滯效應分析中的廣義力矩研究［J］.鐵道學報，2007，29（1）：77－81.Zhang Y H，Li Q.Study on the generalized moment in shear lag effect analysis of box girder［J］.Journal of the China Railway Society，2007，29（1）：77－81.

［10］程祥云.梁橋理論與計算［M］.北京：人民交通出版社，1990.

［11］藺鵬臻，周世軍.基于剪切變形規律的箱梁剪力滯效應研究［J］.鐵道學報，2011，33（4）：100－104.Lin P Z，Zhou S J.Analysis on shear lag effect of box girders based on flange－slab shear deformation law ［J］.Journal of the China Railway Society，2011，33（4）：100－104.

［12］藺鵬臻，周世軍，劉鳳奎.拋物線型剪滯翹曲位移函數引起的附加軸力分析［J］.工程力學，2010，27（8）：90－93.Lin P Z，Zhou S J，Liu F K.Additional axial force analysis caused by parabolical shear lag warping displacement［J］.Engineering Mechanics，2010，27（8）：90－93.

［13］倪元增，錢寅泉.彈性薄壁梁橋分析［M］.北京：人民交通出版社，2000.