減震結構粘滯阻尼器參數優化分析

孫傳智，李愛群，繆長青，黎少華，喬 燕

（1.東南大學 混凝土及預應力混凝土結構教育部重點實驗室，南京 210096；2.宿遷學院 建筑工程系，江蘇 宿遷 223800）

粘滯阻尼器是目前高層建筑結構振動控制中應用較多的結構被動控制裝置之一。在進行粘滯阻尼器減震設計時，可以通過調整阻尼系數和速度指數取得不同的參數組合達到同樣的減震效果，但是不同的參數取值，阻尼器提供的阻尼力相差較大，從而對與其連接的柱內力影響較大，同時阻尼器本身也會出現磨損或損壞，致使減震設計存在不能達到減震要求的隱患［1］。同時粘滯阻尼器的價格主要取決于阻尼力大小，因此在進行粘滯阻尼器減震結構設計時通過粘滯阻尼器參數優化分析，既能保證結構安全，又能盡量降低建造成本，這對于粘滯阻尼器的使用推廣尤為重要。目前已對粘彈性阻尼器的參數優化進行了諸多研究［2－5］，而粘滯阻尼器參數優化研究還比較少，目前多依靠經驗和試算來確定粘滯阻尼器參數，工作量大。響應面分析方法是一種基于試驗設計理論的近似方法，最早由Box等［7］提出，其基本思想是對樣本點處的函數響應計算值或試驗值，用回歸分析法構造一個具有明確表達形式的多項式來表達隱式功能函數。近年來，響應面分析方法已被應用到結構的可靠度評估、模型修正和結構優化［8－12］等方面，其中武和全等［12］將響應面法與試驗設計、有限元分析計算等結合起來，對S型薄壁梁的結構進行抗撞性優化設計。筆者將響應面法與有限元分析相結合，構造參數優化目標函數和約束條件，求得非線性粘滯阻尼器參數最優解。算例應用表明該方法在減震設計過程中具有較強的實用性和有效性。

1 粘滯阻尼器計算模型及減震結構非線性分析

1.1 粘滯阻尼器計算模型

國內外學者對粘滯阻尼器力學模型進行了大量研究［13－15］，美國Taylor公司給出的阻尼力通用表達式為：

1.2 減震結構非線性分析

未設置粘滯阻尼器時，原結構的動力平衡方程為：

式中：［M］為原結構質量矩陣；［C］為原結構阻尼矩陣，采用Rayleigh阻尼；［K］為原結構剛度矩陣；［I］為地震動作用的位置向量；｛x｝、｝分別為節點的位移向量、速度向量和加速度向量；為地震動加速度。當結構采用附加方式設置粘滯阻尼器時，結構的動力平衡方程變為：

式中 ［Cd］為阻尼器提供的附加阻尼矩陣。

求解附加粘滯阻尼器減震結構的控制方程時，出于研究目的和提高計算效率的考慮，可以只進行彈性時程分析，采用快速非線性分析法進行分析［17］。該方法是一種將模態疊加法和增量法組合使用來快速求解只含有少量非線性單元的分析方法，該方法可在保證計算精度的前提下快速提高計算速度［18］，通用有限元軟件SAP2000可以實現快速非線性分析［19］。

2 基于響應面法的減震結構粘滯阻尼器參數優化方法

2.1 減震結構粘滯阻尼器參數優化數學模型

如前所述，在保證結構安全的前提下，應盡量控制附加阻尼器提供的阻尼力，這樣可以降低結構的建造成本，所以在優化設計時以所有粘滯阻尼器提供的阻尼力最小為目標函數，以滿足結構正常使用時的層間位移限值作為約束條件，進行粘滯阻尼器的參數優化，具體形式如下：

設計變量：求粘滯阻尼器阻尼系數Cdi和速度指數αi。

目標函數：所有粘滯阻尼器提供的阻尼力之和∑Fi最小，即min（∑Fi）。

約束條件：各層層間最大位移小于限值，即max（│Δi│）＜［Δ］，［Δ］＝5mm；速度指數α滿足0.2≤αi≤0.8。

2.2 基于響應面法減震結構粘滯阻尼器參數優化步驟

基于響應面進行減震結構粘滯阻尼器參數優化，首先利用響應面法和有限元分析相結合得到各層層間位移和各阻尼器阻尼力的響應面函數，然后進行參數優化。具體來說分為6個步驟：

1）試驗設計。為了確保響應面函數精度，需要以概率論、數理統計和線性代數等為理論基礎進行試驗設計，常用的試驗設計方法有中心復合設計方法和Box－Behnken矩陣抽樣設計方法。根據影響減震效果的主要因素，選擇粘滯阻尼器阻尼系數和速度指數作為自變量xi（i＝1，2，…，L），各阻尼器所提供的最大阻尼力和層間位移作為因變量ym（m＝1，2，…，n），然后采用 Box－Behnken矩陣抽樣法進行試驗設計，確定K組樣本點。

2）有限元計算分析。根據試驗設計的樣本點參數值，利用有限元分析軟件SAP2000進行計算，得到K組層間位移和各阻尼器最大阻尼力變化值ym。

3）參數篩選。在研究的初始階段有可能考慮了所有的參數，如果參數很多，則需要進行參數篩選。參數篩選主要采用方差分析方法，其基本思想是將總變異平方和分解為試驗因素效應與隨機誤差所引起的變異平方和，由此構造出方差分析的F檢驗統計量［20］，找出顯著性參數。

4）響應面擬合。將K組自變量及其對應的K組因變量代入式（4），采用最小二乘法估計多項式系數，得到響應面模型函數。

5）響應面函數精度檢驗。為了驗證響應面模型是否可靠，需對其進行精度檢驗，可采用多重擬合系數R2進行響應面精度檢驗，如式（5）所示，式中代表響應面模型計算值，yj代表有限元模型計算值，代表有限元模型計算值的平均值。R2判定系數在0～1之間取值，R2值越大，則回歸模型就越接近實際情況，如果精度較低則回到第1）步重新進行試驗設計。

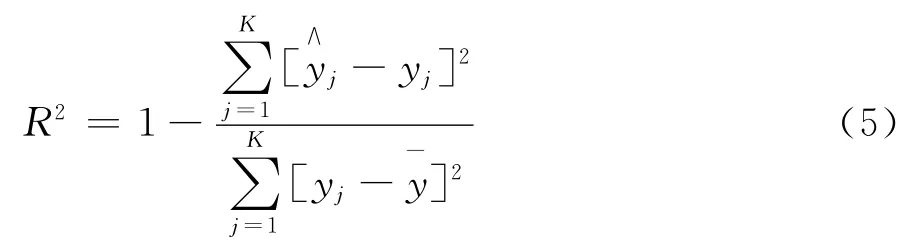
6）粘滯阻尼器參數優化。以層間位移小于限值作為約束條件，所有粘滯阻尼器提供的阻尼力之和最小作為目標函數，建立粘滯阻尼器參數優化數學模型，運用非線性規劃優化方法進行參數優化。

3 算例分析

3.1 算例概況

鋼筋混凝土框架結構，5層，層高5m，跨度6m，柱截面為400mm×400mm，梁截面為250mm×500mm。梁柱材料均為C35混凝土，每層梁柱節點處質量為50kN，輸入地震波為EL－CENTRO，地面運動加速度峰值為140cm／s2，層間位移最大限值為5mm。有限元模型如圖1所示。

圖1 算例有限元模型

3.2 層間位移和阻尼力之和響應面函數

采用Box－Behnken樣本抽樣法進行試驗設計，1～5號阻尼器的阻尼系數為xi（i＝1、3、5、7、9），速度指數為xi（i＝2、4、6、8、10）。各層層間位移為Ri（i＝1、2、3、4、5），阻尼力之和為R6，得到165組樣本點。

應用數理統計的F檢驗法分析所選參數對特征頻率的顯著性，計算各參數的統計特征量的顯著性水平P值，當P＜0.05時，則該參數為顯著。表1為顯著性水平為顯著的參數。由表1可以看出，參數x1、x4、x6和x8對所有因變量的影響都顯著，參數x2和x3對因變量R1、R2、R3和R6的影響顯著，參數x7除了對因變量R2影響不顯著外，對其它因變量均顯著，參數x9僅對因變量R5和R6影響顯著，參數x10對因變量R3、R5和R6影響顯著。此外，部分交叉項和二次項對該模型的顯著性較參數的影響要小，但為了保證精度，在對試驗設計計算得到的樣本數據進行二次多項式響應面回歸時，采用完全二次多項式函數模型。

表1 顯著性檢驗結果

采用完全二次多項式對該樣本值進行響應面回歸即可獲得各層層間位移及各阻尼器阻尼力與各參數之間的響應面函數模型，通過對各響應面模型進行多重擬合系數R2判定，多重擬合系數R2分別為0.9843、0.9756、0.9867、0.9621、0.9513 和0.9769，均大于0.95，能夠滿足參數優化的精度要求。圖2所示R1殘差正態分布概率圖，各殘差點主體部分呈直線，說明誤差呈正態分布。以上分析說明模型擬合度好，利用響應面函數模型精確能夠反映各層層間位移、粘滯阻尼器阻尼力之和與各阻尼器的阻尼系數、速度指數之間的關系，從而能夠保證后續粘滯阻尼器參數優化的精度。

圖2 R1殘差正態分布概率圖

3.3 粘滯阻尼器參數影響分析

限于篇幅，僅以R1為例利用響應面函數分析粘滯阻尼器參數對結構的影響。圖3和圖4分別為1號阻尼器和3號阻尼器對R1的影響曲線圖，即參數x1和x2、x5和x6對因變量R1的影響曲線圖，對于1號阻尼器對R1的影響，從圖3可以看出，R1是隨著阻尼系數的增大而減小，隨著速度指數的減小而減小。但是，從圖4可以看出3號阻尼器對的R1影響關系復雜，在速度指數等于0.2時，R1隨著阻尼系數的增大而減小；在速度指數等于0.8時，R1隨著阻尼系數的增大而增大，反之，在阻尼系數等于30kN·s／m時，R1隨著阻尼系數的增大而增大；在阻尼系數等于150kN·s／m時，R1隨著速度指數的增大而減小。說明如果3號阻尼器參數選擇不合適，有可能使其對R1有放大作用。

圖3 x1和x2對R1的交互影響

圖4 x5和x6對R1的交互影響

由以上分析可知，各阻尼器之間、阻尼器與結構之間的影響關系比較復雜。阻尼器阻尼系數與速度指數的不同取值組合，對減震結構的減震效果有個最優解的問題，需對阻尼器的參數進行優化設計，即能保證結構安全，又使得建造成本最低。

3.4 粘滯阻尼器參數優化

當確定了響應面模型函數后，以各阻尼力之和最小為目標函數，各層間位移和各參數的取值范圍作為約束條件，建立參數優化模型，運用非線性規劃優化方法進行參數優化，即可得到非線性粘滯阻尼器的優化參數，優化后的非線性粘滯阻尼器的參數如表2所示。

通過有限元分析和上文所得的響應面函數可得1～5層層間位移和各粘滯阻尼器阻尼力之和，如表3所示。響應面函數預測所得的層間位移和各阻尼器阻尼力之和與有限元分析所得的相差較小，能夠滿足工程精度要求。

表2 非線性粘滯阻尼器參數優化值

表3 響應面函數預測和有限元分析比較

圖5、6為無控結構和減震結構節點6的位移時程曲線圖和加速度時程曲線圖，從圖中可以看出，結構由于設置了粘滯阻尼器，取得了較好的減震效果。

圖5 節點6位移時程比較

圖6 節點6加速度時程比較

對于非線性粘滯阻尼器阻尼系數和速度指數的取值，選擇如表4所示的5種不同方案進行減震效果比較。第1種方案是基于響應面法優化結果；第2種方案是阻尼系數取值150kN·s／m，速度指數為0.2；第3種方案是阻尼系數取值150kN·s／m，速度指數為0.8；第4種方案是阻尼系數取值90kN·s／m，速度指數為0.5；第5種方案是阻尼系數取值30kN·s／m，速度指數為0.2。

表5為5種不同方案下的參數取值所得的層間位移和各粘滯阻尼器阻尼力之和。可以看出，方案2雖然能夠滿足層間位移限值的要求，但是各阻尼器之和太大，建造成本高；方案3、4、5雖然各阻尼器阻尼力之和較小，但是不能滿足層間位移限值的要求。

4 結 語

1）以一榀鋼筋混凝土框架結構為例，進行了基于響應面法的非線性粘滯阻尼器參數優化設計。結果表明采用簡單的代數公式能夠精確擬合設計變量和響應量之間的復雜關系，把復雜問題顯式化，并且響應面函數精度檢驗表明，響應面函數精度高，能夠滿足優化精度要求。

表4 不同粘滯阻尼器參數取值方案

表5 不同粘滯阻尼器參數取值時的減震效果比較

2）選擇阻尼系數和速度指數作為自變量，結構層間位移、阻尼力之和作為響應值，進行響應面函數擬合。研究表明層間位移和粘滯阻尼力之和與非線性粘滯阻尼器參數取值呈現復雜的非線性關系。

3）結合響應面函數模型，建立目標函數和約束條件，進行非線性粘滯阻尼器參數優化，得到了粘滯阻尼器的參數優化值。該方法精度高、計算量小，過程思路清晰，簡單易行，避免了憑經驗進行參數調整過程中的反復迭代試算。

［1］陳瑜，劉偉慶，陸偉東.線性與非線性黏滯阻尼支撐減震效果的比較［J］.南京工業大學學報：自然科學版，2009，31（6）：45－50.Chen Y，Liu W Q，Lu W D.Comparison of seismicreduced effect between linear and nonlinear viscous damper bracings ［J］.Journal of Nanjing University of Technology：Natural Science Edition，2009，31（6）：45－50.

［2］李正良，李疏影，孫毅.基于遺傳算法的阻尼支撐優化分析［J］.重慶建筑大學學報，2007，29（3）：57－60.Li Z L，Li S Y，Sun Y.Optimum analysis of damper braces based on genetic algorithm ［J］.Journal of Chongqing Jianzhu University，2007，29（3）：57－60.

［3］涂青，徐趙東，彭軍.隔減震結構中黏彈性阻尼裝置的遺傳算法優化分析［J］.東南大學學報：自然科學版，2009，39（1）：73－77.Tu Q，Xu Z D，Peng J.Parametric optimization of viscoelastic device in earthquake isolation and mitigation of structures ［J］.Journal of Southeast University：Natural Science Edition，2009，39（1）：73－77.

［4］Xu Z D，Shen Y P，Zhao H T.A synthetic optimization analysis method on structures with viscoelastic dampers［J］.Soil Dynamics and Earthquake Engineering，2003，23：683－689.

［5］郭勇，孫炳楠，葉尹.多目標優化方法在輸電塔阻尼器布置中的應用［J］.浙江大學學報：工學版，2006，40（10）：1755－1760.Guo Y，Sun B N，Ye Y.Multi－objective optimization approach for damper distribution of transmission towers［J］.Journal of Zhejiang University： Engineering Science，2006，40（10）：1755－1760.

［6］Tandjiria V，Teh C I，Low B K.Reliability analysis of laterally loaded piles using response surface methods［J］.Structural Safety，2000，22：335－355.

［7］Box G E P，Wilson K B.On the experimental attainment of optimum conditions［J］.Journal of the Royal Statistical Society，1951，13（1）：1－34.

［8］Lee S Y，Haldar A.Reliability of frame and shear wall structural systems II：Dynamic loading［J］.Journal of Structural Engineering，2003，129（2）：233－240.

［9］Deng L，Cai C S.Bridge model updating using response surface method and genetic algorithm ［J］.Journal of Bridge Engineering，2010，15（5）：553－564.

［10］ Bayramov F， Tasdemir C， Tasdemir M A.Optimisation of steel fiber reinforced concretes by means of statistical response surface method ［J］.Cement ＆Concrete Composites，2004，26：665－675.

［11］費慶國，韓曉林，蘇鶴玲.響應面有限元模型修正的實現與應用［J］.振動、測試與診斷，2010，30（2）：132－134.Fei Q G，Han X L，Su H L.Response surface based finite element model updating and its application ［J］.Journal of Vibration， Measurement and Diagnosis，2010，30（2）：132－134.

［12］武和全，楊家興，辛勇.基于響應面法的S型薄壁梁抗撞性優化設計［J］.機械科學與技術，2010，29（9）：1132－1136.Wu H Q，Yang J X，Xin Y.Optimal design of S－shaped rail for crashworthiness analysis based on response surface method ［J］.Mechanical Science and Technology for Aerospace Engineering，2010，29（9）：1132－1136.

［13］Makris N，Constantinou M C.Fractional－derivative Maxwell model for viscous dampers ［J］.Journal of Structural Engineering，1991，117（9）：2708－2724.

［14］葉正強，李愛群，程文瀼，等.采用粘滯流體阻尼器的工程結構減振設計研究［J］.建筑結構學報，2001，22（4）：61－66.Ye Z Q，Li A Q，Cheng W R，et al.Study on vibration energy dissipation design of structures with fluid viscous dampers ［J］.Journal of Building Structures，2001，22（4）：61－66.

［15］葉正強，李愛群，徐幼麟.工程結構粘滯流體阻尼器減振新技術及其應用［J］.東南大學學報：自然科學版，2002，32（3）：466－473.Ye Z Q，Li A Q，Xu Y L.Fluid viscous damper technology and its engineering application for structural vibration energy dissipation ［J］.Journal of Southeast University：Natural Science Edition，2002，32 （3）：466－473.

［16］Housner G W，Bergrnan L A.Structural control：past，present and future ［J］.Journal of Engineering Mechanics，1997，123（9）：73－79

［17］陳學偉，韓小雷，毛貴牛，等.粘滯阻尼器在連體高層結構中的抗風減振效果［J］.土木建筑與環境工程，2009，31（5）：74－80.Chen X W，Han X L，Mao G N，et al.Fluid viscous damper technology and its engineering application for structural vibration energy dissipation［J］.Journal of Civil，Architectural ＆ Environmental Engineering，2009，31（5）：74－80.

［18］Wilson E L.Three dimensional dynamic analysis for structures with emphasis on earthquake engineering［M］.Berkeley：Computers and Structures，Inc.，1997.

［19］彭俊生，羅永坤，彭地.結構動力學、抗震計算與SAP2000應用［M］.成都：西南交通大學出版社，2007.

［20］呂棟雷，曹志耀，鄧寶，等.利用方差分析法進行模型驗證［J］.計算機仿真，2006，23（8）：46－48.Lyu D L，Cao Z Y，Deng B，et al.Model verification using variance analysis method ［J］. Computer Simulation，2006，23（8）：46－48.