我國糧食市場價格波動風險研究

王 靜，吳海霞

（西北農林科技大學 經濟管理學院，陜西 楊凌 712100）

一、引 言

近年來，我國糧食價格波動頻繁，尤其是2007年以來，大豆、玉米、生姜等多種農產品價格相繼出現較大幅度的波動。受自然環(huán)境、社會條件、科技水平和市場政策等多種因素的影響，以及農業(yè)本身的自然再生產和經濟再生產相互交織的特點，和農業(yè)生產經營過程的復雜性和不確定性，農業(yè)生產成為風險最為集中的產業(yè)。而對糧食產業(yè)而言，產量風險和價格風險是糧食生產面臨的兩大風險。因此，研究糧食價格波動特征對了解糧食價格波動風險、穩(wěn)定整體糧食市場價格意義重大。

鐘甫寧（1995）認為穩(wěn)定的政治經濟環(huán)境是減少糧食生產人為波動的關鍵因素，統(tǒng)一的市場才能保證糧食儲備制度的正常運行［1］。就糧食市場價格波動的原因：何蒲明、朱信凱（2012）研究表明糧食價格指數與居民消費價格指數存在顯著的正相關，而且具有長期均衡關系，且居民消費價格指數對糧食價格指數的影響遠大于糧食價格指數對居民消費價格指數的影響［2］。羅鋒、牛寶俊（2010）認為國內糧食價格波動主要受農產品生產資料價格推動和自身價格滯后的影響，國際價格波動只對大豆價格影響較為顯著，對小麥和玉米影響較小，對大米幾乎沒有影響［3］。何蒲明、黎東升（2009）認為我國糧食價格波動大于產量波動，價格是產量變化的原因，糧食價格過度波動對國家糧食安全造成了不利影響［4］。對糧食市場價格波動特征的研究：馮云（2008）的研究結果表明糧食價格波動具有顯著的記憶性和持續(xù)性［5］。羅萬純、劉銳（2010）基于ARCH 類模型，研究表明：秈稻、粳稻、大豆價格沒有顯著的異方差效應，小麥和玉米價格波動具有明顯的集簇性［6］。

通過對現有文獻的梳理不難發(fā)現，基于糧食價格的重要性，許多學者已從不同角度進行了研究，但現有研究成果有待進一步發(fā)展和深化：一是目前有關糧食價格波動以宏觀描述為主，計量分析較少；二是近年來我國出現的“玉米瘋”、“豆你玩”、“姜你軍”等現象，表明不同糧食品種其價格波動程度和影響范圍有所差異，對糧食市場的概述很難達到具體問題具體分析的效果，因此根據不同糧食品種、利用ARCH 類模型研究糧食價格波動將更具指導性；三是現有文獻對不同糧食市場間價格的關聯程度和溢出效應研究關注較少，而隨著國家逐步放開糧食市場價格，研究不同市場間的價格聯動效應顯得尤為重要。

基于此，本文將利用ARCH類模型對不同糧食品種的市場價格波動特征進行描述，實證檢驗我國糧食市場價格波動是否具有集簇性和非對稱性、是否具有高風險高回報的特征以及不同糧食市場間的價格聯動效應。由于我國特殊的自然環(huán)境造成的糧食作物的種植中南方水稻北方小麥的顯著地域性差異，以及糧食作物在種植過程中存在共享技術、爭奪土地和資源的特點和北方糧食生產中普遍存在的小麥—玉米—大豆的輪作制，本文將著重分析小麥、玉米、大豆三種糧食作物的價格波動風險，以期為我國北方糧食生產提供可供參考的理論依據。

二、理論模型

（一）價格波動分析

為了刻畫預測誤差的條件方差中可能存在的某種相關性，Engle 于1982年提出了自回歸條件異方差模型，該模型解決了時變方差建模的難題并常用來描述時間序列呈現的條件異方差性和波動集聚性［7］。其基本原理是：對于線性回歸方程（1）式，即

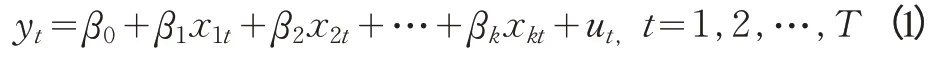
其中，εt為白噪聲過程，滿足：

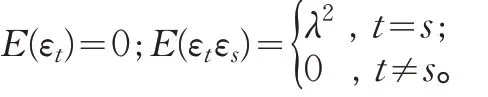
則 隨 機 擾 動 項 ut的 條 件 分 布 為 ：即ut服從以0 均值，為方差的條件正態(tài)分布，前一時刻的擾動項平方即為ARCH項，此過程稱為ARCH（1）過程。

一個自然的延伸是ARCH（P）過程，可以寫為：

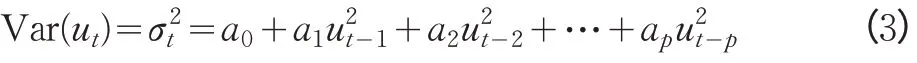
但由于ARCH模型存在滯后期的確定缺乏統(tǒng)一標準的缺陷，且滯后階數過大時，無限制約束的估計常常會違背Var(ut)≥0 的限定條件，因此Bollerslev 將ARCH 模型擴展到廣義自回歸條件異方差模型（GARCH），而在實際應用中，GARCH（1，1）模型由于可顯著降低模型的待估參數，從而降低模型的識別難度而得到普遍認可［8］。

標準的GARCH（1，1）模型為：

Engle、Lilien 和Robins（1987）在GARCH模型的均值方程中加入誤差項的條件標準差，提出了GARCH-M（GARCH-in-Mean）模型［9］：

其中，ρ 是條件標準差的一個倍數，若ρ 為正數表明糧食市場具有高風險高回報的特征。

但是GARCH（1，1）模型的待估方程可能會違背系數非負的條件，且雖然GARCH（1，1）模型能解釋波動的集聚性，但并不能解釋波動的杠桿效應（或稱非對稱性）。因此Zakoian（1994）和Glosten，Jagannathan，Runkle（1993）提出了門限自回歸條件異方差模型（TARCH模型），主要用來刻畫波動的非對稱性［10-11］。TARCH（1，1）模型如下：

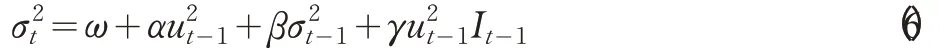
從方程（6）可以看出，若ut-1≥0，則條件方差的系數為α ，即表明價格上漲消息對條件方差的影響為α ；若ut-1＜0，則條件方差的系數為α+γ，即表明價格下跌消息對條件方差的影響為α+γ。如果γ ≠0，則價格波動具有非對稱性。當γ ＞0 時，價格下跌的信息引發(fā)的波動大于價格上漲引發(fā)的波動；當γ ＜0 時，價格上漲的信息引發(fā)的波動大于價格下跌引發(fā)的波動。

（二）聯動效應分析

價格聯動溢出效應即某個市場的大幅波動會傳遞到其他市場，引起其他市場的價格情況發(fā)生變化。本研究采用相關系數計算和Granger 因果檢驗來描述小麥、玉米、大豆市場價格收益率波動的聯動效應。

Granger 因果關系檢驗模型通過受約束的F 檢驗，完成以下回歸的估計：

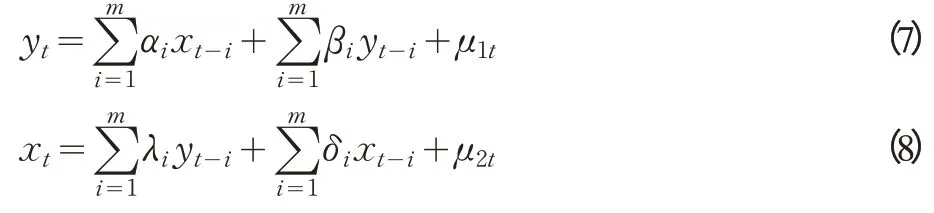
三、樣本數據的選取及數據描述性統(tǒng)計

（一）樣本數據的選取

本文所用數據為全國小麥、玉米、大豆每周批發(fā)市場價格指數，樣本區(qū)間為1998年1月9日到2012年6月22日，數據來源于同花順行業(yè)經濟數據庫。由于數據樣本不完全重合，因此參考Hamao、Masulis and Ng（1990）的研究，將三市場不完全重合的8個周數據刪除，得到統(tǒng)計樣本共計740個［12］。

從圖1 可以看出樣本期間我國小麥、玉米、大豆市場價格呈現明顯的階段性特征。2003年以前全國小麥、玉米、大豆價格基本呈下降趨勢，2003年第四季度起全國小麥、玉米、大豆價格開始逐步回升，并在此后較長的時間內價格保持持續(xù)上升的態(tài)勢。尤其值得注意的是2008年后，玉米和大豆市場價格波動劇烈。例如2009-2011年全國玉米批發(fā)市場價格指數從130 點飆升到240 點，增幅達84.61%；而2008-2009年間大豆價格也出現了十幾年來的高峰，價格指數從100 點上升到252 點。但相比于玉米、大豆價格的大幅波動，2004年至今，小麥價格保持相對平穩(wěn)上升的態(tài)勢，波動較小。

（二）數據的統(tǒng)計性描述

價格收益率以相鄰兩周糧食批發(fā)市場價格指數對數的一階差分表示。以小麥市場為例，計算公式如下：

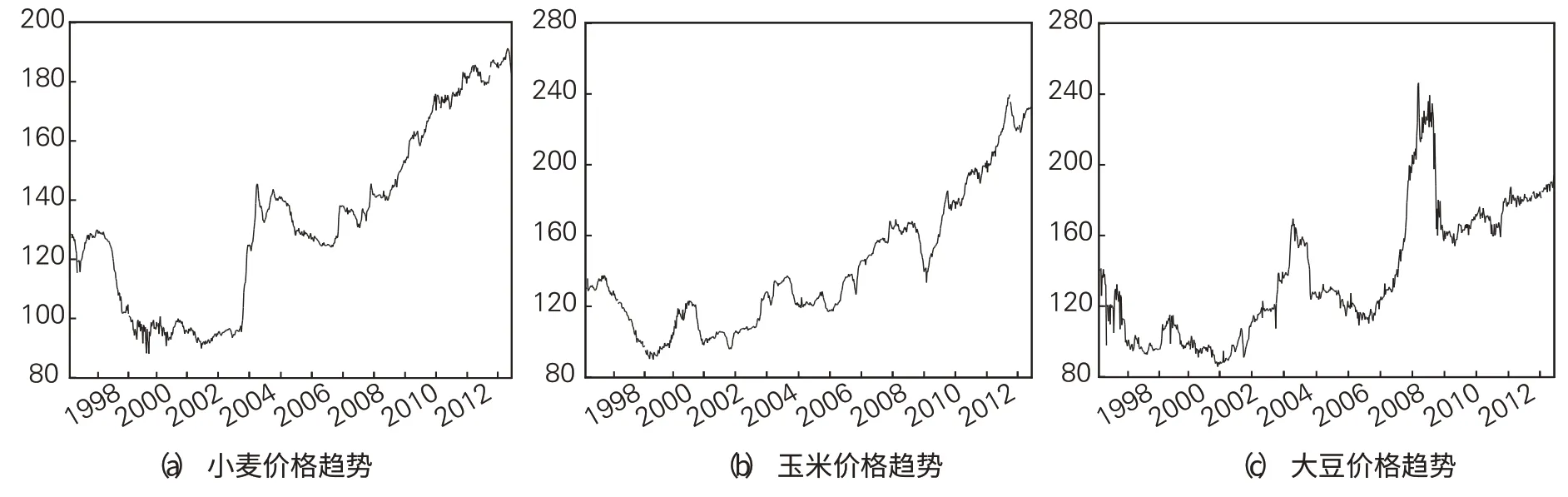
圖1 1998-2012年小麥、玉米、大豆價格趨勢

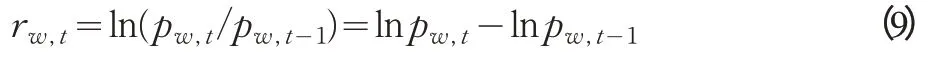
其中， rw,t表示小麥市場在第t 周的價格收益率；ln pw,t、ln pw,t-1分別表示小麥市場在第t 周和t-1 周批發(fā)市場價格指數的對數。同理可以計算出玉米、大豆的市場價格收益率，分別用rc,t、rs,t表示。其統(tǒng)計性描述見表1。

表1 小麥、玉米、大豆價格收益率基本統(tǒng)計量

表1 顯示，樣本期間小麥、玉米、大豆價格收益率的標準差分別為0.0127、0.0139、0.0342，即大豆價格收益率波動最為顯著，小麥市場和玉米市場次之。對比于正態(tài)分布的偏度0，大豆市場價格波動呈明顯左偏性，而小麥和玉米市場價格波動呈明顯右偏性。小麥、玉米和大豆市場價格收益率峰度均大于正態(tài)分布的3，表明三者的價格收益率序列均異于正態(tài)分布，具有典型的尖峰厚尾特征。同時JB統(tǒng)計量也表明三者價格收益率序列均非正態(tài)分布。

圖2 關于小麥、玉米、大豆價格收益率序列走勢圖顯示：小麥、玉米、大豆價格收益率序列均呈現圍繞0 均值上下波動的特征，且大的波動后緊隨大的波動，小的波動后緊隨小的波動，即存在波動的集聚現象，因此價格收益率序列可能存在異方差效應。

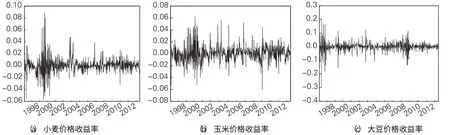
圖2 1998-2012年小麥、玉米、大豆收益率

四、實證結果分析

（一）糧食市場價格波動分析

對小麥、玉米、大豆市場價格收益率序列進行ADF單位根檢驗，選擇滯后階數為0，無截距項和趨勢項，結果表明在5%的置信水平上小麥、玉米、大豆的收益率序列均為平穩(wěn)的時間序列。同時ARCH-LM 檢驗結果表明：選擇滯后階數為2，在5%的顯著性水平下，三市場價格收益率序列均存在顯著異方差效應。

GARCH（1，1）模型對小麥、玉米、大豆收益率條件方差方程的估計結果表明（見表2）：在5%的顯著性水平下，我國小麥市場、玉米市場和大豆市場價格波動均呈現出波動的集簇性和異方差性。GARCH 項的系數均小于1，且ARCH項和GARCH 項的系數之和均小于1，說明我國小麥、玉米、大豆市場波動的持續(xù)性較弱，價格系統(tǒng)本身存在的記憶性將使得過去的波動對未來的影響逐漸消失，糧食市場可根據自身價格機制和市場供求信息，通過一段時間的自我調節(jié)達到市場均衡［13］。相比之下，小麥的市場價格具有最強的記憶性；大豆的市場價格受外界因素的沖擊最大。

GARCH-M模型估計結果表明在5%的置信水平下，小麥市場和大豆市場不具有高風險高回報的特征；玉米市場則要求高風險高回報。若將置信水平擴大到10%，則玉米市場和大豆市場同時呈現出顯著的高風險高回報特征，但小麥市場仍不存在高風險高回報的特征。

TARCH模型估計結果顯示小麥、玉米、大豆的γ 估計值分別為0.1594、0.2057、-0.0131。在5%的顯著性水平下，小麥、玉米的γ 估計值顯著，說明小麥、玉米的價格波動具有顯著的非對稱性，而大豆價格波動不具有非對稱性。同時小麥、玉米的γ 估計值均大于0，表明對小麥市場和玉米市場而言，價格上漲信息帶來的波動遠遠大于價格下跌信息帶來的波動。

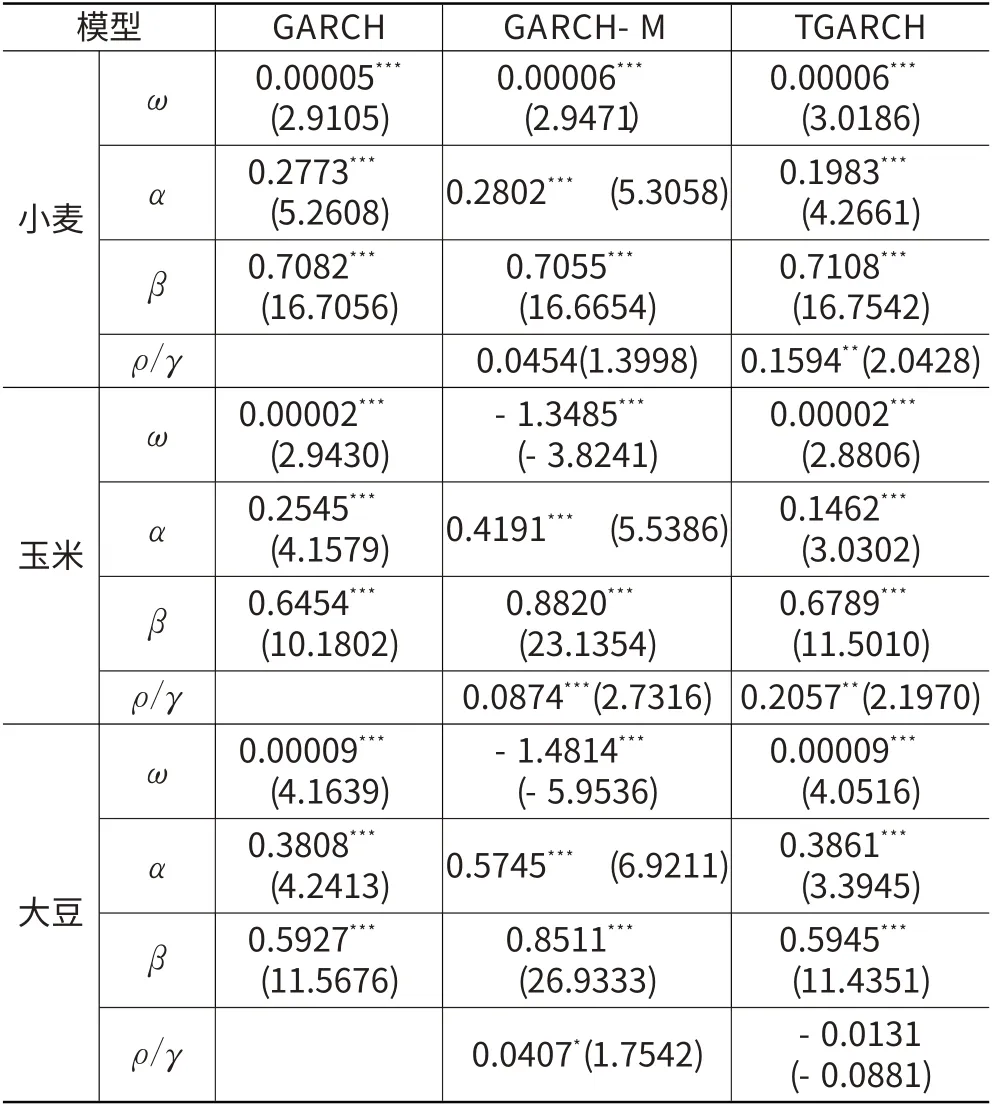
表2 糧食市場GARCH模型的擬合效果

（二）糧食市場波動聯動效應分析

Granger因果關系檢驗主要用于分析經濟時間序列變量之間的因果關系。它的實質在于能否將一個變量的滯后變量引入其他變量的方程中，加入滯后變量后是否使得方程的解釋程度提高。如果某個變量受到其他變量滯后變量的影響顯著，則可判定變量之間具有Granger因果關系。表3給出了在AIC 準則下的最優(yōu)滯后期條件下，三市場價格波動的Granger因果關系檢驗結果。

結果表明：小麥市場價格波動是引起玉米市場和大豆市場價格波動的格蘭杰原因，但玉米、大豆市場價格波動不是小麥市場價格波動的格蘭杰原因；玉米市場價格波動和大豆市場價格波動之間互為格蘭杰原因。

五、結 論

本文采用1998年1月9日到2012年6月22日的全國 小麥、玉米、大豆批發(fā)價格指數的周數據，利用ARCH類模型和Granger 因果關系檢驗對我國糧食價格波動及其溢出效應進行了實證研究。研究發(fā)現，我國小麥、玉米、大豆市場的波動均具有時變性和集簇性。產生波動集簇性的一個可能原因是糧食市場價格序列往往存在自相關關系，即糧食價格走勢易受國家宏觀政策和經濟形勢的影響。小麥市場和玉米市場價格波動的非對稱性特征反映了糧食市場上人們更關心糧食價格上漲的心理，也反映了國家多次出臺政策保護糧價的重要性。雖然糧食市場可以經過自身調節(jié)消除波動，但糧食作為關系國計民生的重要物資，穩(wěn)定糧價，減少波動同樣需要政府的宏觀調控。

小麥、玉米、大豆市場價格波動呈現出顯著的波動集簇性和異方差性表明我國小麥、玉米、大豆市場價格在一定程度上是可以預測的。同時Granger因果關系檢驗表明小麥價格收益率是玉米和大豆價格收益率的Granger原因，因此在一定程度內可以根據小麥市場價格走勢預測玉米及大豆的市場價格；而玉米和大豆價格收益率互為Granger原因表明玉米市場價格和大豆市場價格具有較強的聯動性。在預測玉米市場價格時考慮小麥和大豆的前期價格，在預測大豆市場價格時考慮小麥和玉米的前期價格將有助于提高預測的準確性。

［1］鐘甫寧.穩(wěn)定的政策和統(tǒng)一的市場對我國糧食安全的影響［J］.中國農村經濟，1995（7）：44-47.

［2］何蒲明，朱信凱.我國糧食價格波動與CPI關系的實證研究［J］.農業(yè)技術經濟，2012（2）：83-87.

［3］羅鋒，牛寶俊.我國糧食價格波動的主要影響因素與影響程度［J］.華南農業(yè)大學學報（社會科學版），2010（9）：51-58.

［4］何蒲明，黎東升.基于糧食安全的糧食產量和價格波動實證研究［J］.農業(yè)技術經濟，2009（2）：85-92.

［5］馮云.中國糧食價格波動的實證分析［J］. 價格月刊，2008（2）：41-44.

［6］羅萬純，劉銳.中國糧食價格波動分析：基于ARCH類模型［J］.中國農村經濟，2010（4）：30-37.

［7］Engle R F. Autoregressive conditional heteroskedasticity with estimates of the variance of U.K. inflation［J］. Econometrica，1982，50（4）：987-1008.

［8］Bollerslev T.Generalized autoregressive conditional heteroskedasticity［J］.Journal of Econometrics，1987，31（3）：307-327.

［9］Engle R F，Lilien D M，Robins R P. Estimating time varying risk premia in the term structure：the ARCH-M Model［J］.Econometrica，1987，55（2）：391-407.

［10］Zakoian J M. Threshold Heteroskedastic Models［J］. Journal of Economic Dynamics and Control，1994，18（5）：931-944.

［11］Glosten L R，Jaganathan R，Runkle D.On the relation between the expected value and the volatility of the normal excess return on stocks［J］.Journal of Finance，1993，48（5）：1779-1801.

［12］Hamao Y，Masulis R W，Ng V. Correlations in price changes and volatility across international stock markets［J］.The Review of Financial Studies，1990，3（2）：281-307.

［13］吳海霞，王靜.我國糧食市場價格波動溢出效應研究［J］.農業(yè)技術經濟，2012（10）：14-21.