用光線追跡方法仿真菲涅爾雙棱鏡干涉實驗

董 鍵，崔秀芝

（曲阜師范大學 物理工程學院，山東 曲阜273165）

1 引 言

菲涅爾雙棱鏡干涉實驗是演示分波面干涉原理的基本實驗之一，是傳統實驗項目［1-6］.該實驗測量光波波長的精度不高［7］，其原因主要是對該實驗理論上認識不完善，對于光線如何在光路內傳播，沒有完整的理論公式表達.因為該實驗主要的關注對象是干涉現象并用該現象測量波長，因此，基本的關注點應該是光程和波振幅，本文在研究過程中發現，尋求光程和波振幅的答案，都可以用光線追跡的方法來解決，在此基礎上筆者提出了一種測量光波波長的方法，用來提高該實驗的精度.

2 菲涅爾雙棱鏡實驗的基本原理

菲涅爾雙棱鏡實驗的基本裝置見圖1，激光器發出平行光，經過擴束鏡變成從坐標系原點O發出的發散光束，透過光闌進入菲涅爾雙棱鏡（以下簡稱“棱鏡”，它被x軸平分為上下兩對稱部分，這兩部分分別簡稱為“上棱鏡”和“下棱鏡”），光線經棱鏡折射，到達測微目鏡的分劃板（光屏），來自上下棱鏡的折射光線在分劃板上疊加，形成干涉條紋，可以在目鏡中觀察，并能測量干涉平面上的有關長度.圖1為裝置俯視圖，棱鏡的棱脊垂直于紙面，棱鏡底面垂直于x軸，棱脊可以迎著入射光，也可以背著入射光（圖中顯示后者）.在目鏡分劃板上，干涉條紋垂直于紙面，并沿著y方向周期性擴展.做好該實驗需要調節各個光學器件在光具座上共軸、中心等高.

圖1 菲涅爾雙棱鏡實驗裝置示意圖

根據實驗原理［8］，點光源O經過棱鏡之后將形成2個虛像O1和O2（又稱為虛光源），相距為d，虛像面到目鏡分劃板的距離為L，若光波長為λ，干涉條紋的間距為δ，則

式（1）是討論該實驗的基本依據.

3 光線追跡基本原理

對于由若干界面分割的光學介質系統，2個界面之間充滿了均勻介質，對這樣的系統，光線追跡的基本依據是光的折射定律：

根據該定律，可以由入射光線的方向求出折射光線的方向，方法是將該定律矢量化［9］.令q是光線方向的單位矢量，n是光線所在均勻介質的折射率，定義矢量k＝nq，再令相鄰2種介質界面的單位法矢量為Ω，則可以證明：

這是光線從介質1進入介質2時兩者傳播方向之間的關系.至于界面的法矢量Ω，則可以根據界面方程f（x，y，z）＝0用下式計算：

其中，▽f是函數f的梯度，｜▽f｜是梯度的模.

根據式（3）和（4），可以計算任何光線的傳播路徑，并計算它們在光屏上的落點，進而依據下式求出光線的光程φ：

其中lj是在介質j內光線路徑的長度.

另外，根據光源的性質，可以計算光經過介質之后在光屏上振幅A（y）的分布（見后），然后根據相干疊加的公式計算2束光干涉強度分布I（y）：I（y）＝＋2A1A2cos［2π（φ1-φ2）／λ］，（6）其中光程φ1和φ2也是y的函數.

4 用光線追跡法仿真光線分布

首先計算從點光源O發出的光經棱鏡折射后的分布，以便為后續討論奠定基礎.

模擬計算使用軟件Mathematica，計算中的棱鏡參量如下：折射率n＝1.52，楔角α＝1°，棱鏡厚度L2＝3mm.其他參量是：原點O到棱鏡底面的距離L1＝50mm，棱脊到分劃板的距離L3＝300mm.

圖2是用光線追跡方法計算出的不同發散角的光線到達分劃板的光路情況，從O點以發散角φ＝0（極限意義）出射的光線經折射后在分劃板上被照亮的位置，經過上下棱鏡后分別向對方區域偏折（偏折都是從棱鏡的棱脊開始的），因而合成區域有交疊，形成干涉區，這個區域是可以計算的；在交疊區之外，是未交疊區，不形成干涉.計算該圖所對應的發散角φ＝-2°～2°，可見，形成干涉只需要很小的發散角.

圖2 棱鏡對光的折射仿真圖

5 光線在分劃板上的光程分布

在光線追跡的基礎上，很容易計算來自上下棱鏡的光線在分劃板上的光程分布，見圖3（a），其中曲線φ1表示來自上棱鏡的光程分布，曲線φ2表示來自下棱鏡的光程分布.可見，無論來自棱鏡哪一部分的光線，其光程都不是常量，除了在y＝0處2條光線的光程相等，其他處的光程都不相等，因而有了光程差Δφ＝φ1-φ2，光程差的分布見圖3（b），該圖顯示，光程差是線性分布的.光程差的存在，是形成干涉的必要條件.

圖3 來自棱鏡上下部分的光線在分劃板上的光程分布及光程差

6 關于虛光源

“虛光源”是菲涅爾雙棱鏡干涉實驗的重要概念，其含義是：從光源O發出的光線被上棱鏡折射之后，光線的反向延長線將交于點O1，形成上虛像；光線被下棱鏡折射后形成下虛像O2.這樣從O點發出的所有光線，就等效于從這2個虛像發出，好像棱鏡并不存在［10］.基于該認識，菲涅爾雙棱鏡干涉實驗被等效于2個相干點光源O1和O2所發出光的干涉，就可以套用楊氏雙光源干涉實驗的計算公式［式（1）］.

用光線追跡方法計算被棱鏡所折射光線的反向延長線，見圖4（a），來自上下棱鏡的反向延長線分別匯聚于位置O1和O2，這2個位置在點光源O的右側，與y軸相距δL.粗略看，延長線似乎分別相交于一點，但如果把O1附近區域放大，則如圖4（b）所示，延長線并不相交于一點，而是形成有一定寬度的“細腰”.因此，嚴格來講，虛光源O1和O2并非點光源，使用點光源概念來進行干涉計算會對式（1）造成一定的誤差.對“細腰”的寬度進行考察，以判斷其具體粗細.方法是尋找“細腰”最細的位置界面，計算每條延長線與該界面交點的y值并乘以2，作為兩虛光源的間距d，這樣可以得到d的分布曲線，見圖5（a），從該曲線上可大致得出d＝0.943 2～0.943 9mm，“細腰”的寬度為0.7μm，遠小于人眼的分辨能力，對于該實驗的測量精度，可以將O1和O2當做點光源來看待.

圖4 虛光源及局部放大圖

因為“細腰”可以當做點光源，所以，通過“細腰”O1和O2的任何2條光線反向延長線之間的距離都可以作為2個虛光源的間距d.選擇2條水平延長線之間的距離作為d，確定d的具體做法見圖5（b），該圖是經過上棱鏡折射光線的斜率k與光線在分劃板上位置y的關系曲線，是直線，該直線與y軸的交點對應k＝0，相應的y值乘以2作為d.

圖5 虛光源間距d隨著發散角φ的分布和確定虛光源間距的方法

關于虛光源的性質，還可以考察其間距d和虛像所在平面的位置δL隨棱鏡位置L1的變化關系，見圖6，可見兩者的關系都是線性的.要注意的是，δL隨L1變化很小，可以近似認為虛像面的位置是不變的.

圖6 虛光源間距d和虛像面的位置δL隨棱鏡位置L1的變化

7 式（1）的模擬證明

有了圖3光程差的結果，可以計算分劃板上干涉光的強度分布，因為光程差是線性的，所以光強隨y的分布是周期性的（見后），其周期就是干涉條紋的間距δ.根據式（1），在光的波長λ已知和虛像面到分劃板的距離L固定的情況下，δ與d成反比，二者的乘積等于λL.模擬計算λ＝0.6μm和L＋δL＝300mm情況下δ與d的關系，見圖7，經過擬合，證明二者符合反比關系，比例系數為0.179 373，容易驗證，該數值非常接近λL，證明式（1）的近似程度很好，也證明虛光源概念的引入是合理的.

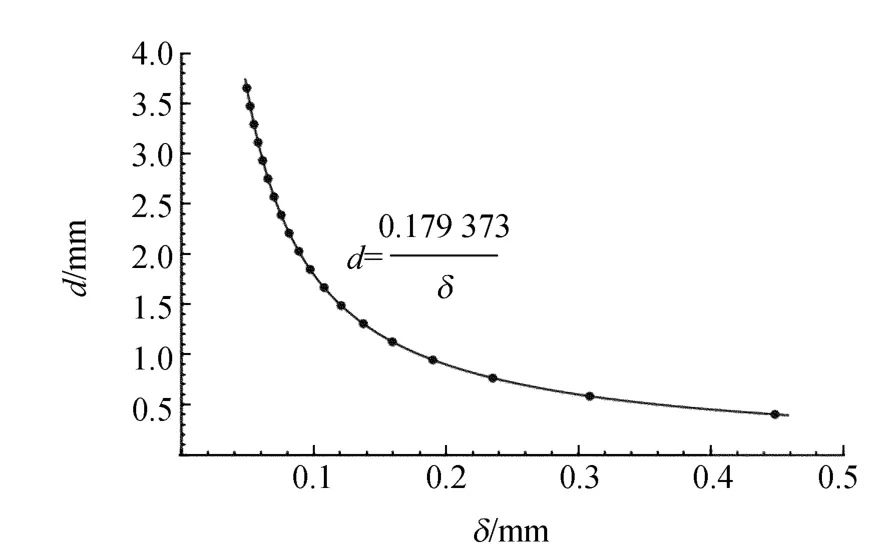
圖7 虛光源間距與條紋間距的模擬關系

8 凸透鏡使虛光源成像

二次成像法要在棱鏡與分劃板之間加1個凸透鏡，使2個虛光源成像于分劃板.圖8模擬了該過程，所使用的凸透鏡焦距為64.5mm，左極點與棱鏡的棱脊相距30mm.圖8（a）表明，上下棱鏡的折射光經過凸透鏡后匯聚的位置是顛倒的，其位置用箭頭指示；將該位置附近區域放大，即為圖8（b），它表明光線也并非匯聚成一個點，而是匯聚成“細腰”，這在透鏡有球差的情況下是可以預料的.不過，該圖真正的含義在于：“細腰”在x方向擴展范圍很大，在此范圍內，像寬都差不多，因而很難準確判定像的位置，這正是二次成像法測量光波波長誤差大的原因所在.

圖8 加凸透鏡所成虛光源的像及其局部放大圖

9 測量光波波長的方法

通過光線追跡清楚該實驗的細節后，作者提出了測量光波波長的方法，該方法可以提高波長測量的精度，而且不需要知道棱鏡的具體參量.下面是該方法的原理.

根據虛光源的性質，可以得到

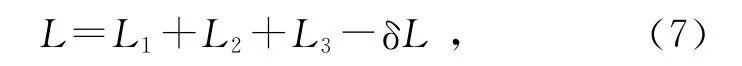
根據經驗，式（7）中右邊的長度量很難測定，直接測量會引起L較大的誤差，尤其是在使用激光光源的情況下，O點的位置難以確定.把式（1）和（7）結合起來，得到

虛光源的間距d只與L1有關，在固定L1的情況下，改變L3，就可以測量出不同的δ，從而構成δ-L3的線性關系，通過擬合得到系數b，

這樣得到的b具有L3的測量精度，因為光具座上的毫米刻度尺可以測量出4位有效數字.雖然L3并不能代表分劃板的位置，但因為可以把這一固定的偏差歸于截距a中，所以測量精度得以保證.于是對應某個L1的距離L就以較高的精度被計算出來，

為了測量2個虛光源的間距d，需要測量分劃板上干涉區的y向寬度w，這在使用激光光源的情況下可以得到較高的精度.因為仿真研究表明，干涉條紋的間距δ與L1有關，L1越大，δ越小，二者是反比關系.因此，實驗時取較大的L1，讓δ盡可能地小，干涉條紋盡可能地細，這樣，干涉區內就容納了足夠多的條紋，其邊界比較容易確定.在此條件下，可以測量光線經過棱鏡的最大偏折角tanβ，原理見圖9.圖中，保持光屏位置不變，棱脊的位置為x1，相應干涉區寬度為w1；移動棱鏡，使棱脊的位置變為x2，干涉區寬度相應變為w2，則有如下關系：

雖然棱脊的絕對位置很難測定，但位置的差值x2-x1卻具有光具座刻度尺的測量精度，而w2-w1具有測微目鏡的測量精度，所以tanβ的測量精度得到提高，

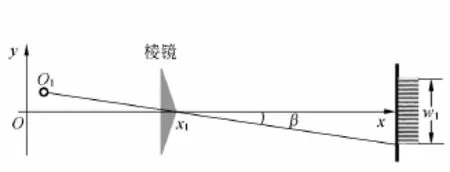
圖9 測量光線最大偏折角tanβ

在測量了tanβ之后，根據如下關系計算虛光源的間距d，

于是，光波的波長為

為了充分利用分劃板的有效寬度（通常為8mm），適當地調整L3，使干涉區寬度接近有效寬度.

10 關于折射光在分劃板上的振幅分布

根據式（6），要計算干涉光強，就需要知道來自2條光線的振幅A1（y）和A2（y），這在光源性質已知的情況下是可以計算出來的.假定激光器輸出的光束橫截面上光強分布均勻，則通過光線追跡可以證明兩點（證明過程從略）：

1）激光經過球面擴束鏡之后光能是各向同性發散的；

2）經過棱鏡之后光線在分劃板上的位置y與光線的發散角φ成線性關系.

這2點結合起來，就得到如下結論：

在忽略光線與分劃板之間的夾角與直角有微小偏離的條件下，折射光的振幅和強度都是均勻分布的，即A1（y）＝A2（y）＝A0.于是，

相位差Δφ的分布見圖3（b），它是線性分布的，因而強度I（y）在分劃板上是周期性分布的，相鄰2條亮紋之間的間距δ相同.

11 結束語

菲涅爾雙棱鏡干涉實驗能夠用光線追跡方法進行全面仿真，由此可以深入全面地了解該實驗的細節，結論直觀可靠，并在此基礎上提出了光波波長測量的方法，提高了測量精度，而且不需要知道棱鏡的具體參量（例如折射率、楔角和厚度），對做好該實驗很有啟發性.

［1］金重.費涅耳雙棱鏡實驗精度的提高［J］.河北大學學報，1981（1）：89-90.

［2］秦庚生，侯永忠.菲涅爾雙棱鏡干涉實驗的改進［J］.物理實驗，1987，17（2）：67-69.

［3］張國英，徐克耀.用雙棱鏡“等位移法”測光波波長［J］.首都師大學報，1997，18（1）：45-48.

［4］周亞俊，王秦鏡，馬秀芳，等.關于“雙棱鏡必須均勻照亮”的深入探討［J］.物理實驗，2003，23（7）：46-48.

［5］廖立新，劉生長，米賢武.用雙棱鏡測激光波長的簡單方法［J］.物理實驗，2007，27（7）：34-35.

［6］葛松華，唐亞明.菲涅耳雙棱鏡干涉實驗中距離參數的研究［J］.大學物理，2010，29（4）：43-45.

［7］王明吉，張利巍，王曉莉.雙棱鏡干涉4種實驗方法的研究與探討［J］.物理實驗，2008，28（4）：25-27.

［8］周殿清.大學物理實驗［M］.武漢：武漢大學出版社 ，2005：260-265.

［9］張以謨.應用光學［M］.北京：機械工業出版社，1982：6-7.

［10］袁成衛，劉廷賢，張海新.費涅耳雙棱鏡干涉實驗中的“虛光源”［J］.物理實驗，1999，19（3）：48-49.