N階幻方的構造算法及其代數性質
2013-12-01 05:34:54周云才長江大學計算機科學學院湖北荊州434023
長江大學學報(自科版) 2013年19期
關鍵詞:性質
周云才,孫 方 (長江大學計算機科學學院,湖北 荊州434023)
陳 忠 (長江大學信息與數學學院,湖北 荊州434023)
1 N階幻方的定義
定義1 將自然數1到N2,排列N行N列的方陣,使每行、每列及2條主對角線上的N個數的和都等,這樣的方陣稱為N階幻方。
2 N階幻方的構造算法
對N階幻方幻方的構造,分為3種情況:N為奇數、N為4的倍數、N為其他偶數(4n+2的形式)。對文獻 [1]中的算法進行整理,得到下面的算法:
2.1 N為奇數
N為奇數時,N階幻方A構造如下:
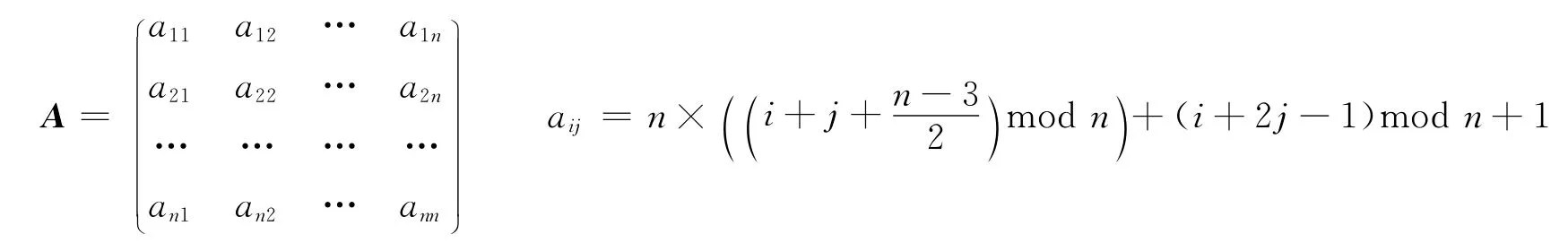
2.2 N為4的倍數
N=4k時,N階幻方A構造如下:
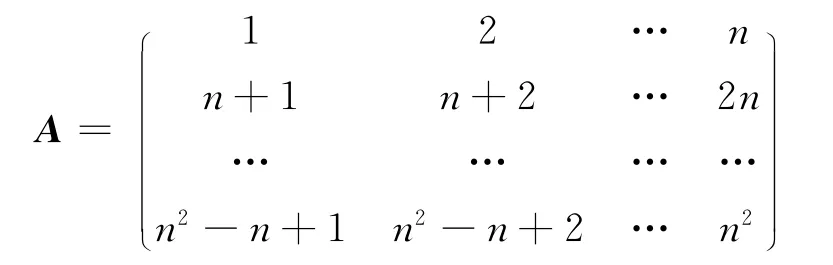
2.3 N為其他偶數
N=4k+2時,N階幻方A構造如下:
(1)利用N為奇數時的算法求一個2k+1階的幻方矩陣B=(bij)。
(2)構造A:① 當i,j均不超過2k+1時,aij=bij;② 當i≤2k+1<j≤n時,aij=bi,j-2k-1+2(2k+1)2;③ 當j≤2k+1<i≤n時,aij=bi-2k-1,j+3(2k+1)2;④ 當i>2k+1,j>2k+1時,aij=bi-2k-1,j-2k-1+ (2k+1)2。
(3)調整:①將1到k列與第3k+4到n列(當3k+4>n時,此類列為空)的元素的后面2k+1個元素放到前面,前面的2k+1個元素放到后面,即:
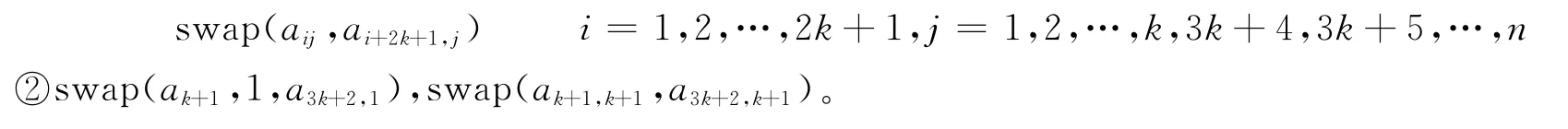
以n=10為例,演算過程如下,n=10,k=2:
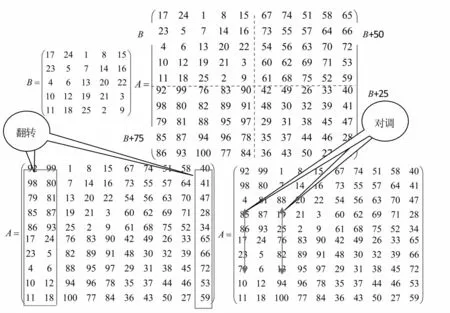
3 N階幻方的代數性質
性質1(N階幻方的秩[1]) 對于利用以上算法構成的幻方,奇數階幻方是滿秩的;4k階幻方的秩是3;4k+2階幻方的秩是2k+3。
證明 實對稱矩陣ATA的特征值的正根稱為實矩陣A的奇異值[2],由此不難證明是n階幻方的奇異值。
下證其最大性。對于A的任一奇異值σ,有非零向量x= (x1,x2,…,xn)T使得ATAx =σ2x。不妨設max{|x1|,|x2|,…,|xn|}=1,且|x1|=1,于是:
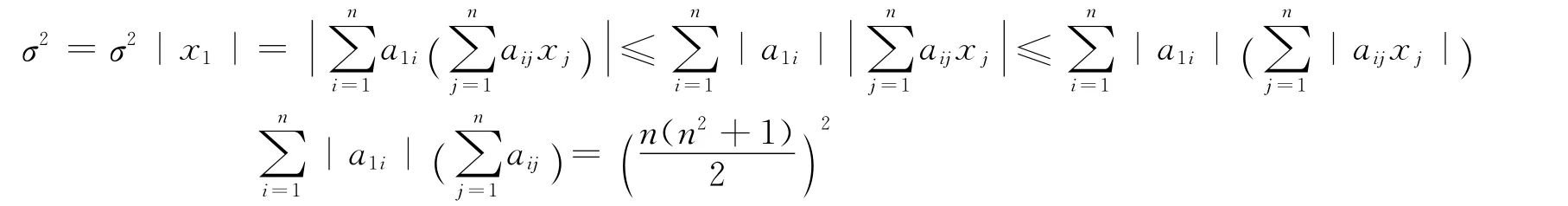
猜你喜歡
中學生數理化·高三版(2023年6期)2023-07-19 11:17:53
數學物理學報(2022年6期)2022-12-15 08:45:02
上海師范大學學報·自然科學版(2022年3期)2022-07-11 03:05:59
數學雜志(2021年6期)2021-11-24 11:12:00
中學生數理化(高中版.高二數學)(2021年5期)2021-07-21 02:14:46
數學年刊A輯(中文版)(2021年1期)2021-06-09 09:31:56
中等數學(2020年6期)2020-09-21 09:32:38
山東農業工程學院學報(2019年11期)2020-01-19 02:49:10
數學物理學報(2019年6期)2020-01-13 06:07:52
中等數學(2019年6期)2019-08-30 03:41:46

