一種改進的DY共軛梯度法及其全局收斂性

王安平 （長江大學工程技術學院基礎教學部，湖北 荊州434020）

馬 爍 （荊州理工職業學院基礎課部，湖北 荊州434000）

考慮無約束優化問題：

式中，f：Rn→R連續可微。共軛梯度法是求解該問題的一類有效算法。一般的共軛梯度法迭代公式為：

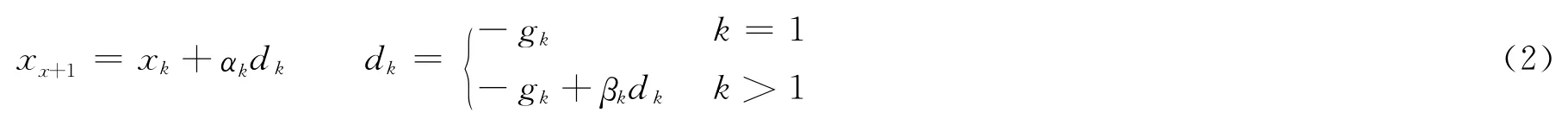
式中，x1為初始點；dk為搜索方向；αk是由某種線性搜索或由特定公式計算出的步長因子；βk為標量；g（x）＝ ▽f（x），gk＝ ▽f（xk）。共軛梯度法的關鍵是選取αk和βk，不同的αk和βk決定了不同的共軛梯度算法。常用選取αk的線搜索是標準Wolfe線搜索，即選取αk＞0滿足：

式中，δ和σ是滿足0＜δ＜σ＜1的常數。而βk的選取公式常用的有：

對應的共軛梯度法依次為FR方法［1］、PRP方法［2］、HS方法［3］、CD方法［4］、LS方法［5］和 DY 方法［6］。

在眾多共軛梯度法中，為了保證下降方向，許多學者都做了深入的研究。文獻 ［7］提出了一種改進的DY共軛梯度法，參數βk的計算公式為：

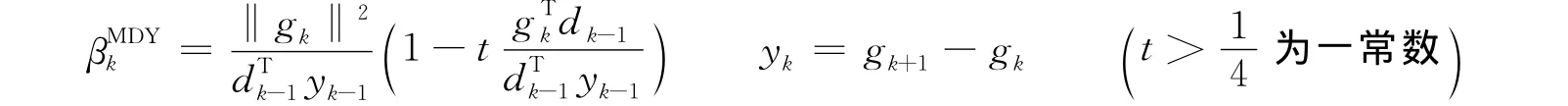
受文獻［7］的啟發，筆者在MDY方法的基礎上，給出了一個新的參數βk的取法，即：

1 改進的DY算法及其充分下降性

改進的DY算法如下：

步1 給定初始點x1∈Rn，ε＞0，d1＝－g1，令k＝1；

步2 若‖gk‖≤ε，則停止迭代；否則轉入步3；

步3 由式（3）求得αk；

步4 計算xx＋1＝xk＋αkdk，若 ‖gk＋1‖ ≤ε，則算法停止，否則轉步5；

步5 利用式（4）計算βk＋1。計算dk＋1＝－gk＋1＋βk＋1dk，置k＝k＋1，轉步2。

定理1 設迭代方向由：

證明 當k＝0時，dT0g0＝－‖g0‖2，結論成立。

當k≥0時，dk＝－gk＋βNMDYkdk－1兩邊與gk做內積：

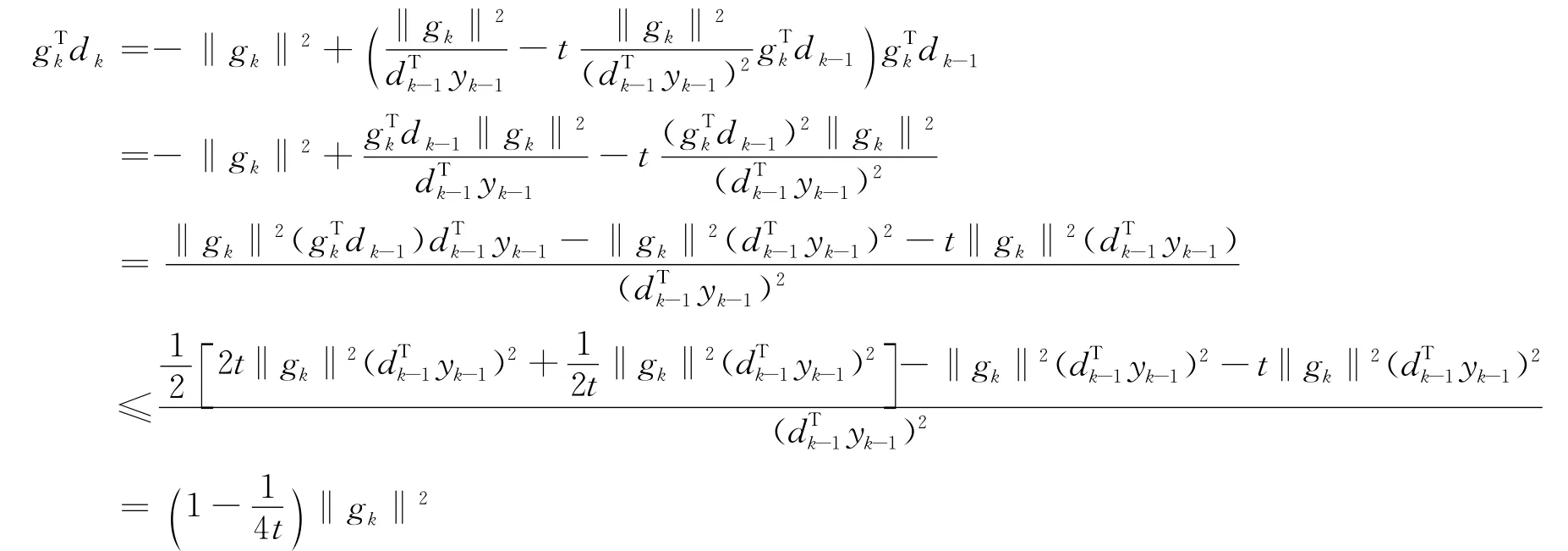
2 算法的全局收斂性

下面筆者將在一定的假設條件下證明NMDY算法的全局收斂性。假設條件（A）如下：

（1）水平集L1＝ ｛x∈Rn｜f（x）≤f（x1）｝有界，其中x1為初始點；

（2）在水平集L1的一個鄰域U內，f（x）是連續可微的，其梯度g（x）是lipschitz連續的，即存在常數L＞0使：

‖g（x）－g（y）‖ ≤L‖x－y‖ ?x，y∈U引理1 設目標函數f（x）滿足假設A，序列｛xk｝由式（2）產生，其中βk由（4）計算，αk滿足式（3），則。此關系式稱為Zoutendijk條件。

證明 由定理1及式（3），則有：

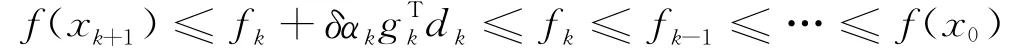
則式（6）說明了函數列｛fk｝有界。再由定理1及式（3）和假設條件（A）中的第2個條件，則有：

再聯合式（3）可以得到：

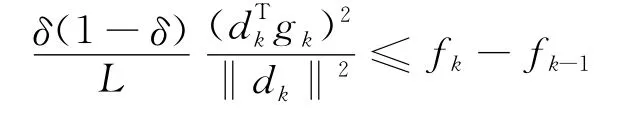
又因為函數列｛fk｝有界，所以有：

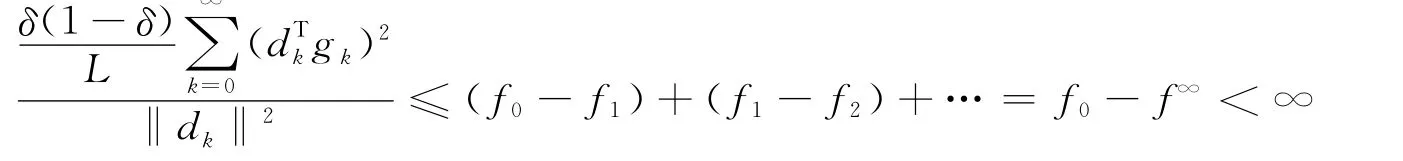
定理2 設目標函數f（x）滿足假設條件A，序列｛xk｝由式（2）產生，其中βk由式（4）計算，αk由式（3）確定。假設存在一個正數α＊，滿足αk≥α＊，則有：

證明 由假設A中的（1），則存在一個常數M＞0使得：

由式（8）和αk≥α＊，可以得到：

由式（9）及引理1和定理1的結論，可以得到式（7），即定理2得證。