“溶解熱測定”實驗數據處理的雙倒數模型
王 曦,曾 馨,韓 翔,張業中,吳愛斌 (長江大學化學與環境工程學院,湖北荊州434023)
“溶解熱測定”是物理化學中的一個經典實驗,其實驗原理是采用電熱補償法來測定硝酸鉀在水中的積分溶解熱Qs,其他3種熱效應 (微分稀釋熱、微分溶解熱和積分稀釋熱)則可通過Qs~n0(n0=nH2O/nKNO3;nH2O、nKNO3分別為水和硝酸鉀物質的量)曲線求得。學生在實驗數據處理時需要先做Qs~n0圖,再做某些點的切線來求算微分溶解熱,若學生運用圖解法[1]作圖,則會使數據處理步驟變得十分繁瑣,并且作圖效果差,給實驗結果帶入了較大的人為誤差。故教學中通常要求學生選取合適的數學模型并借助Origin軟件[2-7]對實驗數據進行擬合,得出相應的Qs~n0解析式,再根據解析式求得Qs對n0的導數Q′s,代入相應的n0值,可求得該點處的斜率,即得到不同n0的微分沖淡熱,由點(n0,Qs)和該點處的斜率可求出唯一的直線方程,進而得到所求得的截距,即微分溶解熱。常見的數學模型有對數模型[8]、多項式模型[9]、一次指數衰減模型[10]:

然而這些模型未能完全反映硝酸鉀溶解時的一些特征,物質溶解是溶質的微粒 (分子或離子)離開固體 (液體)表面擴散到溶劑中以及溶質的微粒 (分子或離子)和溶劑分子生成溶劑化物的過程。前一過程是吸熱過程,后一過程放熱過程。對不同的溶質來說,吸收的熱量和放出的熱量并不相等,故不同物質溶解表現出吸熱或放熱現象。硝酸鉀溶解時,因為它和水分子的結合不穩定,吸收的熱量比放出的熱量多,就表現為吸熱,在溶解時,溶液的溫度就降低。
對于硝酸鉀溶解熱測定實驗,結合實驗事實及相關文獻,硝酸鉀溶解時有以下特征:①當溶劑量趨于無窮大,即n0趨于無窮大時,Qs為一常數[11];②由實驗數據作圖可觀測到,隨著n0的增大曲線斜率逐漸變小;③當n0等于零,即溶劑(水)不存在時,硝酸鉀不存在微粒擴散以及微粒溶劑化作用,由此得出當n0等于零時,Qs也應為零。
為此,筆者根據以上特征提出了雙倒數模型1/Qs=A/n0+B。
1 熱測定實驗步驟及數據
該實驗使用南京桑力電子設備廠生產的SWC-RJ溶解熱測定裝置,實驗步驟如下:①在電子天平上依次稱取8份質量為2.5,1.5,2.5,3.0,3.5,4.0,4.0,4.5g的硝酸鉀 (應預先研磨并烘干),記下準確數據并編號。②在臺式天平上稱取216.2g蒸餾水于杜瓦瓶內,放入磁珠,擰緊瓶蓋并放到反應架固定架上。③將O型圈套入傳感器,調節O型圈使傳感器浸入蒸餾水約100mm,把傳感器探頭插入杜瓦瓶內。④按下 “狀態轉換”鍵使儀器處于測試狀態。調節 “加熱功率調節”旋鈕,使功率P=2.5W左右。調節 “調速”旋鈕使攪拌磁珠為實驗所需要的轉速。⑤實驗時,先讓加熱器正常加熱,使溫度高于環境溫度0.5℃左右,按 “溫差采零”鍵,儀器自動清零,立刻打開杜瓦瓶的加料口,按編號加入第1份樣品并同步計時,觀察溫度變化,等溫差回到零時,加入第2份樣品,以此類推,加完所有的樣品。⑥實驗結束,按 “狀態轉換”鍵,使儀器處于“待機狀態”。將 “加熱功率調節”旋鈕和 “調速”旋鈕左旋到底,關閉電源開關,拆去實驗裝置。實驗數據記錄見表1。
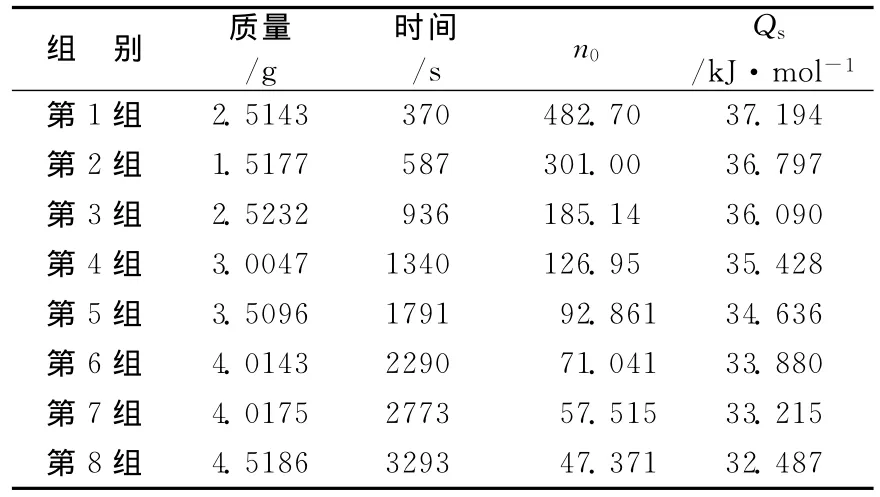
表1 硝酸鉀溶解熱的實驗數據
2 數據擬合及討論
通過Origin7.5軟件對表1數據進行處理,對Qs,n0分別進行對數模型擬合、多項式模型擬合、一次指數衰減模型擬合和雙倒數模型擬合,各種模型Origin擬合圖如圖1所示。
從圖1可看出,指數衰減模型、對數模型擬合所用參數均為3個,其擬合相關系數均比雙倒數模型擬合的相關系數要低,說明這2種模型的擬合準確度均沒有雙倒數模型擬合的準確度高。且當n0趨于零時,對數模型與指數衰減模型的Qs均不為零,不符合前述特征③:“當n0等于零時,Qs也為零”;在n0趨于無窮大時,對數模型的Qs為無窮大,不符合前述特征①:“當n0趨于無窮大時,Qs為一常數”。
從圖1中還可看出,多項式模型的擬合相關系數最大,但多項式模型擬合所用參數最多 (4個),其高擬合精度是用更多的待定參數而達到的,擬合步驟較多,Qs~n0解析式較復雜,對后續數據處理不便,尤其對Origin軟件初學者有一定難度。且多項式模型在n0趨于無窮大時,Qs為無窮大;當n0趨于零時,Qs不為零,不符合前述特征①與特征③。
而雙倒數模型在形式上更簡潔,所用參數只有2個,比上述3種模型的擬合參數都少,準確度也較高,且符合前述特征①、②和③。當n0=200時,雙倒數模型Qs=36.25kJ/mol,結果與實驗要求值Qs=(35.00±2)kJ/mol符合較好。雙倒數模型的線性化處理以及相對較少的待定參數,使應用該模型作圖、分析更為方便,尤其相較于多項式模型。為驗證雙倒數模型的可行性,將雙倒數模型對文獻 [12]已公布的數據進行了擬合,得1/Qs=0.18559/n0+0.02681(R2值為0.9940),當n0=200時,雙倒數模型Qs=36.05kJ/mol比原文Qs=36.17kJ/mol更接近實驗準確值Qs=35.00kJ/mol。

圖1 Qs~n0關系曲線
3 結 語
一個好的數學模型應既能夠與實驗數據相接近,又能夠反映一些實驗事實。選取合適的數學模型進行擬合來確定Qs~n0解析式,可以有效減小數據處理中的人為誤差,是一種行之有效的手段。在KNO3溶解熱測定實驗中,數據處理階段應用何種數學模型更為適合尚無明確的結論。筆者系統地比較了用于處理KNO3溶解熱測定實驗數據的一些常見數學模型,提出了更適合學生運用、形式簡潔、參數更少、準確度較高的雙倒數模型1/Qs=A/n0+B,方便了學生對該實驗的數據處理。

