拉格朗日微分中值定理的證明與坐標旋轉
余勝春
(武漢科技大學理學院,湖北 武漢430081)
拉格朗日(Lagrange)微分中值定理的證明,一般都是采用構造一個滿足羅爾(Rolle)定理的3個條件的輔助函數,利用羅爾定理來證明的[1]。其輔助函數具有其一定的規律性。
1 拉格朗日微分中值定理證明中輔助函數的構造與推廣
對于拉格朗日中值定理函數y=f(x)不具有羅爾定理所滿足的f(a)=f(b)的條件,要用羅爾定理來證明它,就必須通過構造輔助函數來消除這一因素,使其滿足羅爾定理的條件。
1)一般構造 采用在曲線y=f(x)的縱坐標上減去端點為A(a,f(a)),B(b,f(b))的弦所在的直線的縱坐標。事實上,弦AB所在的直線方程為:

其兩者之差為:
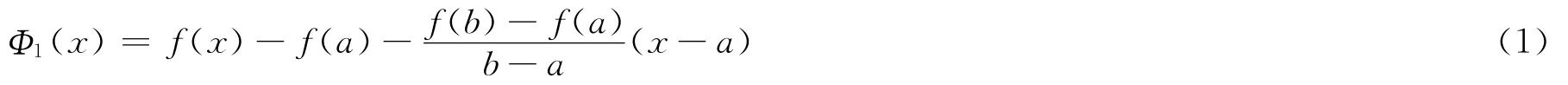
式(1)便是常見于定理證明中的輔助函數,它滿足羅爾定理的3個條件。
2)推廣 ①用曲線y=f(x)的縱坐標上減去平行于弦AB的所有直線的縱坐標得到的函數也可以作為拉格朗日中值定理證明中的輔助函數。一般地:,滿足羅爾定理的條件。

進而:

② 從拉格朗日中值定理所要證明的結論“存在ξ∈(a,b),立”出發,也可以構造出滿足羅爾定理條件的輔助函數來。即構造一個[a,b]上滿足羅爾定理條件的函數Φ4(x),要求Φ4(x)在x=ξ處的導數,故令:

即可。事實上,對Φ4(x)也有滿足羅爾定理的條件。
2 坐標系的旋轉變換
從幾何的角度來看,也會提出能不能用坐標系的旋轉變換,使得曲線y=f(x)的端點A(a,f(a)),B(b,f(b))在新坐標系下的函數值相同,從而運用羅爾微分中值定理來證明這一定理呢?回答是肯定的。解決這一問題的關鍵在于函數y=f(x)經過坐標系的旋轉變換,即在新的坐標系下,是否仍然滿足羅爾微分中值定理的條件。
事實上,坐標系xoy上的函數y=f(x)在[a,b]上滿足拉格朗日微分中值定理的條件,但經過坐標系旋轉:
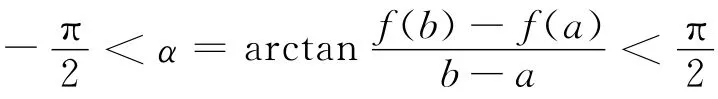
后,即在新坐標系下有閉區間上連續,且端點處的函數值相同,但不一定滿足羅爾微分中值定理在開區間(a,b)內可微的條件。
例1 函數f(x)=x3-32+4在[-1,1]上滿足拉格朗日微分中值定理的條件,經過坐標系旋轉:
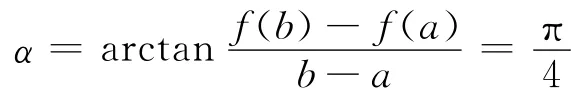
后,有:

由式(5)所確定的函數的導數為:

定理1 在坐標系XOY下的函數y=f(x)在[a,b]上滿足拉格朗日微分中值定理的條件,且不存在x0∈(a,b),使:
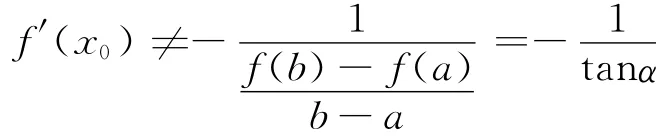
時,即曲線y=f(x)在(a,b)內無垂直于弦AB的切線,則坐標系xoy經過旋轉α角后得到的新坐標系XOY,則函數y=f(x)在新坐標系XOY下滿足羅爾定理的條件,可以證明拉格朗日微分中值定理的結論。
證明 函數y=f(x)在[a,b]上滿足拉格朗日微分中值定理的條件,將xoy旋轉α角后,得到新坐標系XOY,有:

由式(6)所確定的函數在x∈[a,b]上顯然連續,且:
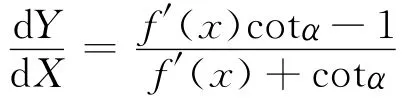
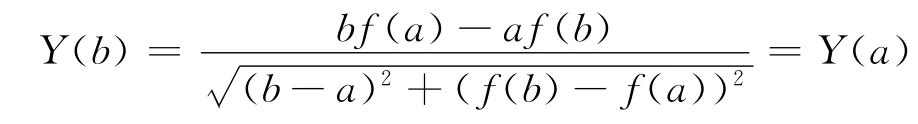
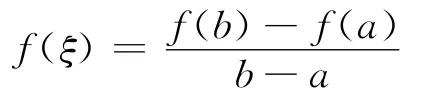
定理2 在坐標系xoy下的函數y=f(x)在[a,b]上滿足拉格朗日微分中值定理的條件,且存在x0∈(a,b)使:

時,則坐標系xoy經過旋轉α角后得到的新坐標系XOY,則函數y=f(x)在新坐標系XOY下不滿足羅爾定理的條件,也可以通過坐標系旋轉來證明拉格朗日微分中值定理的結論。
證明 若函數y=f(x)的圖形在點(x0,f(x0))處有垂直于弦AB的切線,即滿足:

可以過(x0,f(x0))作一條平行與弦AB的直線l:y-f(x0)=f′(x0)(x-x0)交曲線y=f(x)于x1≠x0處,不防設x1<x0,則y=f(x)在[x1,x0]上滿足定理1的條件,即可通過坐標系旋轉變換來證明存在
綜上所述,拉格朗日定理的證明,無論函數y=f(x)在[a,b]上有無垂直于弦AB的的切線,均可以通過坐標系的旋轉變換來完成。
[1]同濟大學數學系 .高等數學[M].第6版 .北京:高等教育出版社,2007.

