幾何參數和強度參數對邊坡三維穩定性的影響

宋維勝，李江騰

(1.湖南張家界市水利局，湖南 張家界，427000；2.中南大學 資源與安全工程學院，湖南 長沙，410083)

我國是巖土工程大國，各種類型的邊坡失穩及滑坡災害是我國國民經濟建設和發展中亟待解決的問題。穩定性分析是邊坡工程中最基本最重要的研究內容。近年來，隨著計算機技術的發展，采用基于強度折減的數值分析方法進行穩定性分析成為新的趨勢，并且該方法已在二維邊坡穩定性研究中得到廣泛應用[1?6]，如：Griffiths等[1]論述了如何將強度折減技術與理想彈塑性有限單元法相結合分析二維邊坡的穩定性；鄭穎人等[4?5]對強度折減法基本理論和如何提高計算精度進行了研究。隨著計算精度的提高，這種方法受到國內巖土工程界和設計部門的廣泛關注，將該方法的應用范圍不斷擴大，如應用于均質的土坡、土基用具有結構面的巖坡與巖基。但在實際工程中，由于存在大量大型復雜邊坡，基于平面應變模型的二維分析方法不能適用于該類實際三維邊坡穩定性的研究。為適應新的工程需求，人們迫切需要將分析維度由二維向三維拓展，為此，一些研究者對三維邊坡穩定性進行了研究，如：宋雅坤等[7]將強度折減法應用于三維邊坡穩定性分析中，通過3個典型的工程算例對幾種常用的屈服準則進行比較；譚曉慧等[8]基于有限元強度折減法，對邊坡的彈塑性材料非線性及大變形幾何非線性進行了分析，并考慮了邊坡的三維變形情況。這些研究主要是進行邊坡變形穩定性的三維計算，而對其三維效應以及三維效應的變化規律和影響因素的研究較少。為此，本文作者采用FLAC3D有限差分程序[9?10]，對邊坡的三維效應及其影響因素進行分析，探討邊坡寬高比、邊坡角、巖土體內摩擦角和黏結力對于邊坡安全系數和滑動面的影響。其中，邊坡三維安全系數的定義采用強度折減法的定義，即不斷折減邊坡的安全系數直至邊坡達到臨界失穩狀態，此時，對應的折減系數即為邊坡的安全系數。

1 數值計算模型

建立邊坡體三維計算模型如圖1所示。邊坡各維度尺寸見表1。圖1和表1中：L1為坡腳到左端邊界的距離；L2為坡頂與右邊界的距離；W為邊坡體寬度；β為邊坡坡角；H為邊坡體高度；W=(0.25～10)H，用于比較不同寬度對邊坡體穩定系數及滑動面形態的影響。張魯渝等[11]在研究有限元強度折減法計算精度時認為：邊界范圍在數值計算方法中對結果的影響比在傳統極限平衡法中更敏感，并通過算例給出了比較合理的邊坡體尺寸范圍。在本文模型中，坡腳到左端邊界的距離L1為坡高H的1.5倍，上、下邊界總高D+H為2H。計算參數如下：彈性模量為30.0 MPa，泊松比為0.3，容重為18.8 kN/m3，黏結力為30.0 kPa，內摩擦角為 20°。考慮到在實際邊坡中，全約束邊界為非常典型的邊界約束類型[12]。

由其得到的邊坡穩定系數及滑動面形狀與二維情形及三維平面應變模型應有明顯的差異，故本文在分析邊坡體三維效應分析時，統一采用全約束邊界條件。采用強度折減法進行三維安全系數的計算，采用計算不收斂判據判定邊坡的臨界破壞狀態[13]。

表1 邊坡計算模型尺寸Table 1 Geometry size of slope model

2 邊坡穩定的三維效應分析

為分析比較邊坡體在三維效應下的穩定性及滑動面情況，設計不同比較算例，計算邊坡體寬度W、邊坡坡角β、黏結力c、內摩擦角φ等因素對邊坡穩定性的影響，并將三維計算模型得到的結果與二維情況的結果進行比較。

2.1 邊坡寬度對三維邊坡安全系數的影響

傳統的邊坡穩定性分析方法是建立在平面應變模型基礎上的，在平面應變模型中，邊坡在三維寬度方向的長度(即邊坡寬度)被假定為無限大。若邊坡的寬度W與邊坡高度H相比較小，則平面應變假設不再滿足，邊坡體側面范圍內的約束情況將對邊坡穩定性及滑動面產生不可忽視的影響，此時，必需引入三維效應分析。為驗證邊坡寬度 W 的影響，本文設計了40組比較算例，邊坡寬高比W/H由0.25變化至10.00。算例中，取邊坡坡角β為30°，45°，60°及75°共4組值，以分析不同坡角下寬高比對邊坡穩定系數的影響。黏結力c=30 kPa，內摩擦角φ=20°。使用FLAC3D有限差分軟件，基于強度折減法原理計算邊坡穩定性，得到寬高比對三維邊坡安全系數的影響，結果見圖2。從圖2可見：隨著寬高比W/H的增大，邊坡穩定系數明顯減小，最后趨于一定值；且坡角越小，穩定系數變化區間越大；當W/H＜3時，得到的邊坡穩定系數明顯較大；當W/H＞3時，三維效應影響逐漸減弱，得到的穩定系數也趨近于二維模型得到的結果。這是由于在全約束邊界條件下，邊坡體側面為固定端，在寬度較小時，邊坡體受側面約束的挾制作用明顯；隨著寬高比的增大，側面約束條件對土體的挾制作用減弱；當寬高比很大時，側面約束對土體的挾制作用可忽略，此時，可將三維問題簡化為平面應變問題。

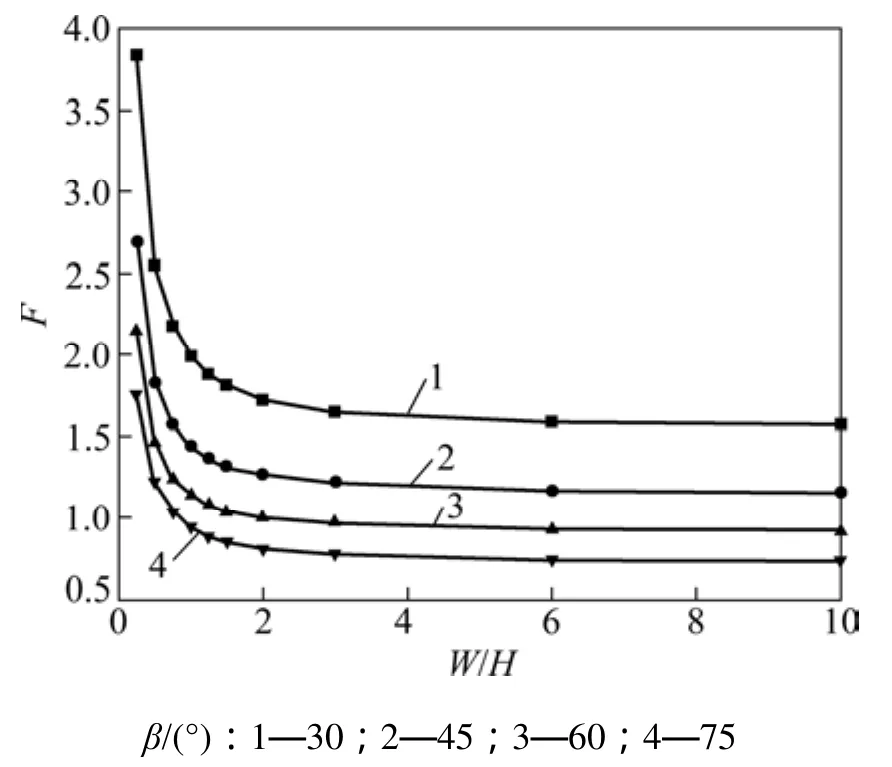
圖2 寬高比W/H對三維邊坡安全系數F的影響Fig.2 Effect of ratio of width to height on factor of safety of three-dimensional slope

2.2 邊坡角對三維邊坡安全系數的影響

邊坡角是影響邊坡穩定性的重要因素，隨著坡角的增加，邊坡的穩定性將降低。為了突出三維效應的影響，邊坡寬高比W/H選用0.5，1.5和6.0共3種情形，坡角變化范圍為15～75°，將得到的邊坡角對三維邊坡安全系數F的影響與二維結果進行比較，如圖3所示。從圖3可見：邊坡穩定系數F隨著坡角的增大而明顯減小；在寬高比相同時，三維模型得到的安全系數均比二維模型得到的安全系數高，當W/H=0.5時，安全系數平均高 70.3%，最大高 93.5%；當 W/H=1.5時，安全系數平均高20.7%，最大高29.0；%；當W/H=6時，安全系數平均高 5.3%，最大高 7.1%；寬高比越小，邊坡的三維效應越突出，得到穩定系數偏差越大；在坡角越小、寬高比相同時，穩定系數偏差越大即邊坡的三維效應越明顯，當坡角增大時，曲線呈收斂狀，偏差逐漸減小。

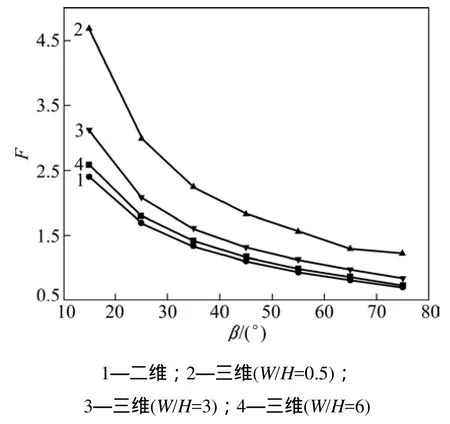
圖3 邊坡角β對三維邊坡安全系數F的影響Fig.3 Effect of slope angle on factor of safety of three?dimensional slope

2.3 內摩擦角對三維邊坡安全系數的影響

邊坡寬高比選用W/H=0.5，內摩擦角變化范圍為15°～45°。算例中取坡角 β=45°，黏結力 c=30 kPa，得到內摩擦角對于邊坡穩定性的影響如圖4所示。從圖4可見：采用三維計算模型得到的穩定系數比二維的大，安全系數最大偏差為69.6%，平均偏差為50.8%；并且隨著內摩擦角的增大，二者的偏差越來越小，說明邊坡的三維效應逐漸減弱。

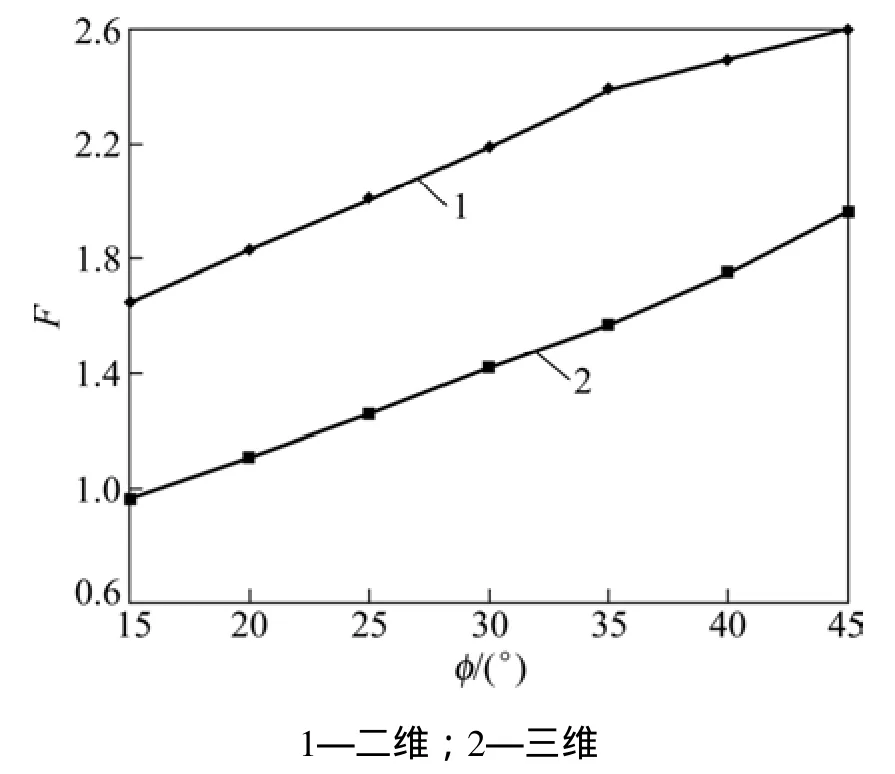
圖4 內摩擦角φ 對三維邊坡安全系數F的影響Fig.4 Effect of friction angle on factor of safety of three-dimensional slope

為揭示不同邊坡體處于臨界破壞狀態時滑動面的形狀差異，增加內摩擦角φ=2°及φ=8°共2個算例，針對每個算例在邊坡對稱面處進行剖切，使用文獻[14]中的滑動面確定方法，得到內摩擦角對邊坡滑動面形狀的影響如圖5所示。從圖5可以看出：當內摩擦角很小時，滑體的體積很大，滑動面的位置較深，滑出點的位置不在坡腳處，而是離坡腳有一定距離；隨著內摩擦角的增大，滑體的體積變小，滑動面的位置變淺，滑出點經過坡腳；當內摩擦角很大時，滑動面貼近于坡面，接近于淺層滑動。這是由于對于內摩擦角很小的邊坡材料(如淤泥質土等)，材料間摩擦作用力較小，發生破壞時將觸發更深層滑坡，因而滑坡體的體積更大；而對于內摩擦角較大的邊坡(如巖質邊坡)，發生破壞時將更多地表現為淺層的崩塌甚至局部風化，無法觸發深層的滑坡，因而滑出點位置距坡腳較遠，滑體體積較小。

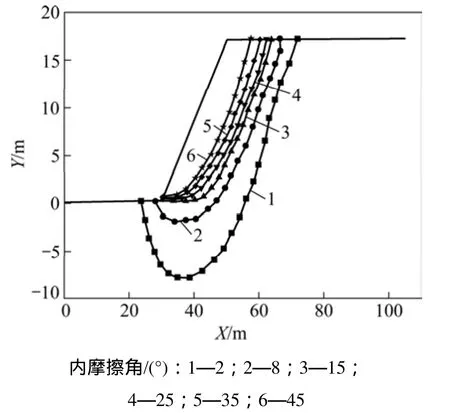
圖5 內摩擦角對邊坡滑動面形狀的影響Fig.5 Effect of friction angle on slip surface of slope

2.4 黏結力對三維邊坡安全系數的影響

為研究邊坡黏結力對邊坡安全系數的影響，邊坡寬高比選用W/H=0.5，黏結力變化范圍為10～70 kPa，算例中取坡角 β=45°。將得到的結果與二維結果進行比較，結果見圖6。從圖6可看出：在分析邊坡穩定系數隨著黏結力變化的影響時，采用三維計算模型得到的安全系數明顯比二維模型得到的安全系數大，最大偏差為82.8%，平均偏差為65.8%；采用這2種模型得到的結果偏差隨著黏結力的增加而增大，說明三維效應隨著黏結力的增大而增大。

為分析黏結力變化對滑動面形狀及滑出點位置的影響，另增加c=250 kPa比較算例，在邊坡體對稱面處取剖切面。不同黏結力條件下得到的滑動面形狀見圖7。從圖7可見：隨著黏結力的增大，滑坡體體積明顯增大，邊坡破壞表現為深層滑動；當材料黏結力很小時(如巖質邊坡情形)，邊坡表現為淺層滑動。

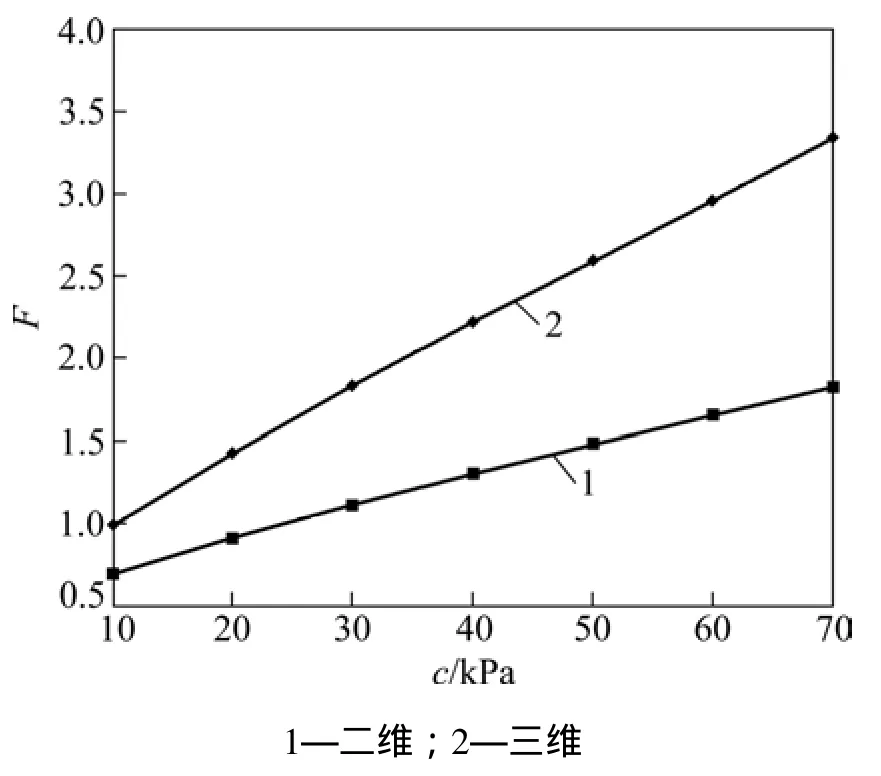
圖6 黏結力c對三維邊坡安全系數F的影響Fig.6 Effect of cohesion on factor of safety of three-dimensional slope

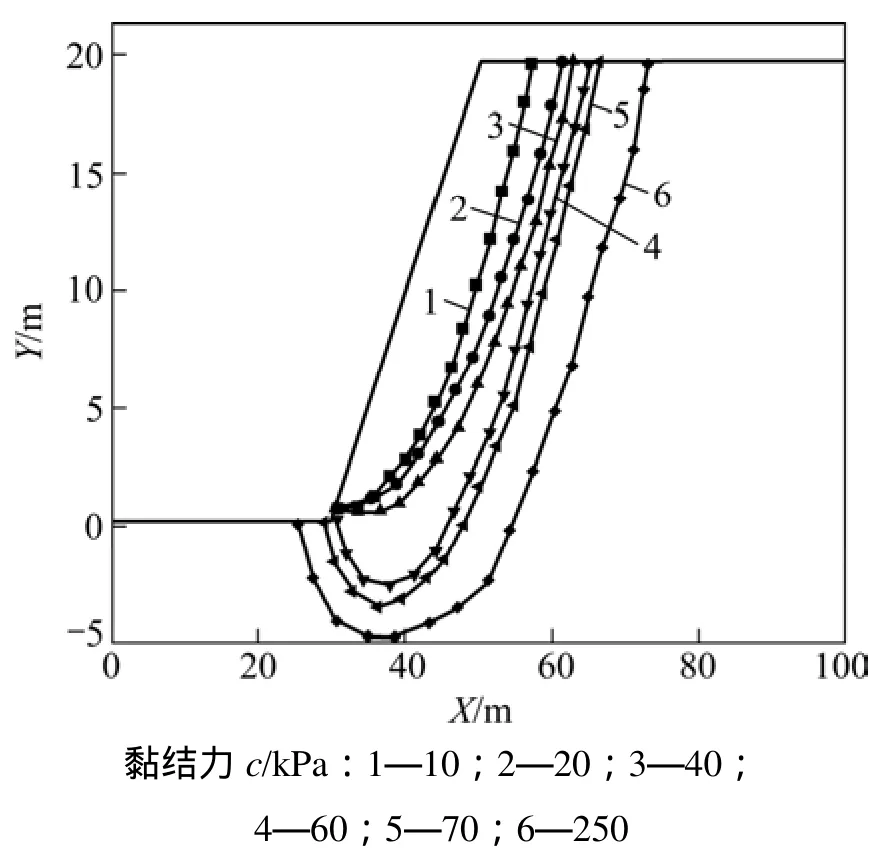
圖7 不同黏結力下的邊坡臨界滑動面Fig.7 Slip surface of slopes under different cohesion

3 結論

(1) 隨著寬高比W/H的增大，邊坡穩定系數明顯減小，最后趨于一定值，且坡角越小，穩定系數變化區間越大；當W/H＞6時，邊坡問題簡化為平面應變問題是可行的；寬高比越小，邊坡的三維效應越突出，當W/H＜3時，三維效應的影響不能忽視。

(2) 當坡角越小時，在不同工況下，穩定系數偏差越大，即邊坡的三維效應越明顯；坡角增大時，曲線呈收斂狀，偏差逐漸減小。

(3) 隨著內摩擦角的增大，三維模型與二維模型的邊坡安全系數偏差越來越小，邊坡的三維效應逐漸減弱；隨著內摩擦角的增大，邊坡滑動由深層滑動轉變為淺層滑動。

(4) 三維效應隨著黏結力的增大而增大。隨著黏結力的增大，邊坡滑動由淺層滑動轉變為深層滑動，滑動面越來越緩。

[1]Griffiths D V, Lane P A.Slope stability analysis by finite elements[J].Geotechnique, 1999, 49(3): 387?403.

[2]Dawson E M, Roth W H, Drescher A.Slope stability analysis by strength reduction[J].Geotechnique, 1999, 49(6): 835?840.

[3]Matsui T, San K C.Finite element slope stability analysis by shear strength reduction technique[J].Soils and Foundations,1992, 32(1): 59?70.

[4]鄭穎人, 趙尚毅.巖土工程極限分析有限元法及其應用[J].土木工程學報, 2005, 38(1): 92?104.ZHENG Yingren, ZHAO Shangyi.Limit state finite element method for geotechnical engineering analysis and its applications[J].China Civil Engineering Journal, 2005, 38(1):92?104.

[5]鄭穎人, 趙尚毅, 張魯渝.用有限元強度折減法進行邊坡穩定分析[J].中國工程科學, 2002, 4(10): 57?78.ZHENG Yingren, ZHAO Shangyi, ZHANG Luyu.Slope stability analysis by strength reduction FEM[J].Engineering Science, 2002, 4(10): 57?78.

[6]宋二祥.土工結構安全系數的有限元計算[J].巖土工程學報,1997, 19(2): 1?7.SONG Erxiang.Finite element analysis of safety factor for soil structures[J].Chinese Journal of Geotechnical Engineering, 1997,19(2): 1?7.

[7]宋雅坤, 鄭穎人, 趙尚毅, 等.有限元強度折減法在三維邊坡中的應用研究[J].地下空間與工程學報, 2006, 2(5): 822?827.SONG Yakun, ZHENG Yingren, ZHAO Shangyi, et al.Application of three dimensional strength reduction FEM in slope[J].Chinese Journal of Underground Space and Engineering, 2006, 2(5): 822?827.

[8]譚曉慧, 王建國, 王印.邊坡穩定的非線性有限元分析[J].巖土力學, 2008, 29(8): 2047?2050.TAN Xiaohui, WANG Jianguo, WANG Yin.Nonlinear finite element analysis of slope stability[J].Rock and Soil Mechanics,2008, 29(8): 2047?2050.

[9]林杭, 曹平, 宮鳳強.位移突變判據中監測點的位置和位移方式分析[J].巖土工程學報, 2007, 29(9): 1433?1438.LIN Hang, CAO Ping, GONG Fengqiang.Analysis of location and displacement mode of monitoring point in displacement mutation criterion[J].Chinese Journal of Geotechnical Engineering, 2007, 29(9): 1433?1438.

[10]Grasselli G.3D Behaviour of bolted rock joints: Experimental and numerical study[J].International Journal of Rock Mechanics& Mining Sciences, 2005(42): 13?24.

[11]張魯渝, 鄭穎人, 趙尚毅, 等.有限元強度折減系數法計算土坡穩定安全系數的精度研究[J].水利學報, 2003(1): 21?27.ZHANG Luyu, ZHENG Yingren, ZHAO Shangyi, et al.The feasibility study of strength reduction method with fem for calculating safety factors of soil slope stability[J].Journal of Hydraulic Engineering, 2003(1): 21?27.

[12]Griffiths D V, Marquez R M.Three-dimensional slope stability analysis by elasto-plastic finite elements[J].Geotechnique, 2007,57(6): 537?546.

[13]林杭, 曹平, 李江騰, 等.邊坡臨界失穩狀態的判定標準分析[J].煤炭學報, 2008, 33(6): 643?647.LIN Hang, CAO Ping, LI Jiangteng, et al.Analysis of the standards for critical failure state of slope[J].Journal of China Coal Society, 2008, 33(6): 643?647.

[14]LIN Hang, CAO Ping, GONG Fengqiang, et al.The directly searching method for slip plane and its influential factors based on the critical state of slope[J].Journal of Central South University of Technology, 2009, 16(1): 131?135.