六自由度振動(dòng)試驗(yàn)系統(tǒng)運(yùn)動(dòng)極限*
張步云,陳懷海,賀旭東,郭家驊
(1.南京航空航天大學(xué)機(jī)械結(jié)構(gòu)力學(xué)及控制國(guó)家重點(diǎn)實(shí)驗(yàn)室 南京,210016)
(2.上海宇航系統(tǒng)工程研究所 上海,201108)
引 言
在實(shí)驗(yàn)室條件下用振動(dòng)臺(tái)進(jìn)行振動(dòng)測(cè)試試驗(yàn)是對(duì)產(chǎn)品在運(yùn)輸、使用環(huán)境中經(jīng)受振動(dòng)環(huán)境的最佳人工模擬[1]。單軸振動(dòng)試驗(yàn)技術(shù)在工程領(lǐng)域應(yīng)用廣泛,局限性也很明顯。文獻(xiàn)[2-3]指出單軸振動(dòng)試驗(yàn)無(wú)法完全復(fù)現(xiàn)外場(chǎng)故障,加大量級(jí)的補(bǔ)償措施易導(dǎo)致試件過試驗(yàn)或過設(shè)計(jì),難以實(shí)現(xiàn)不同振動(dòng)方向載荷的準(zhǔn)確迭加。賀旭東[4]指出在對(duì)大型試件進(jìn)行振動(dòng)試驗(yàn)時(shí),單軸振動(dòng)臺(tái)無(wú)法提供足夠的推力,難以達(dá)到規(guī)定的試驗(yàn)量級(jí),且單點(diǎn)激勵(lì)不利于實(shí)現(xiàn)振動(dòng)分布的均勻性,使應(yīng)力和位移分布不夠合理。Freeman[5]指出通過單軸振動(dòng)試驗(yàn)的設(shè)備無(wú)法承受多維的外場(chǎng)振動(dòng)環(huán)境。事實(shí)上,從嚴(yán)格意義來(lái)說(shuō),產(chǎn)品在使用過程中的振動(dòng)環(huán)境大都是多自由度的,單軸振動(dòng)試驗(yàn)難以準(zhǔn)確描述產(chǎn)品的真實(shí)工況。
從20世紀(jì)60年代開始,研究重點(diǎn)轉(zhuǎn)移到多軸振動(dòng)系統(tǒng)領(lǐng)域,并取得一系列進(jìn)展。Whiteman等[6-7]研究了多維振動(dòng)試驗(yàn)方法,指出多軸振動(dòng)試驗(yàn)?zāi)苡行p少試驗(yàn)時(shí)間且提供更真實(shí)的應(yīng)力分布情況。美國(guó)的Wyle實(shí)驗(yàn)室、MTS公司和Team公司等都開始研究多軸振動(dòng)環(huán)境試驗(yàn)技術(shù),且應(yīng)用到實(shí)際產(chǎn)品的生產(chǎn)中。Wyle實(shí)驗(yàn)室為Hill空軍基地研制的三軸向六自由度電動(dòng)振動(dòng)系統(tǒng)是目前較先進(jìn)的電動(dòng)式多軸振動(dòng)系統(tǒng)[8]。關(guān)廣豐等[9-10]就六自由度液壓振動(dòng)試驗(yàn)系統(tǒng)的控制策略進(jìn)行了理論和試驗(yàn)研究。嚴(yán)俠等[11]以三軸向六自由度液壓振動(dòng)臺(tái)系統(tǒng)為典型被控對(duì)象,建立了三軸六自由度液壓振動(dòng)臺(tái)隨機(jī)振動(dòng)控制仿真系統(tǒng)。陳建秋等[12-13]對(duì)六自由度地震模擬振動(dòng)臺(tái)的控制系統(tǒng)進(jìn)行了研究。這些研究多以多軸液壓振動(dòng)系統(tǒng)為主。
在振動(dòng)試驗(yàn)中關(guān)心的是多軸振動(dòng)系統(tǒng)的試驗(yàn)?zāi)芰Γ绕涫橇杂啥入妱?dòng)振動(dòng)系統(tǒng)。若已知振動(dòng)系統(tǒng)的相關(guān)參數(shù),求得臺(tái)面的最大運(yùn)動(dòng)能力(即能達(dá)到的最大位移或最大加速度)是研究人員關(guān)心的問題。另一方面,給定一定的試驗(yàn)條件,振動(dòng)臺(tái)能否達(dá)到這樣的指標(biāo)是試驗(yàn)?zāi)芊癯晒Φ年P(guān)鍵。筆者根據(jù)斯圖爾特平臺(tái)模型[14-16]的分析方法,以六自由度電動(dòng)振動(dòng)系統(tǒng)臺(tái)面的運(yùn)動(dòng)極限問題進(jìn)行建模研究,建立各振動(dòng)臺(tái)與臺(tái)面之間的位移關(guān)系,為多軸振動(dòng)系統(tǒng)試驗(yàn)的實(shí)際應(yīng)用提供理論依據(jù)。
1 振動(dòng)系統(tǒng)幾何模型
在實(shí)際振動(dòng)環(huán)境中,大部分產(chǎn)品有6個(gè)自由度的運(yùn)動(dòng),其中:3個(gè)平動(dòng)自由度分別為沿x軸、y軸和z軸的移動(dòng);3個(gè)轉(zhuǎn)動(dòng)自由度為繞軸x旋轉(zhuǎn)的Rx、繞y軸旋轉(zhuǎn)的Ry和繞z軸旋轉(zhuǎn)的Rz。圖1為六自由度振動(dòng)簡(jiǎn)化模型。

圖1 六自由度振動(dòng)模型圖
在具有8個(gè)獨(dú)立的單軸振動(dòng)臺(tái)的六自由度振動(dòng)系統(tǒng)中,每個(gè)自由度的響應(yīng)都是由8個(gè)振動(dòng)臺(tái)共同激勵(lì)產(chǎn)生的[17]。圖2為美國(guó)Hill空軍基地SVIC中心的多臺(tái)多軸(MEMA)系統(tǒng),由2個(gè)x向振動(dòng)臺(tái)、2個(gè)y向振動(dòng)臺(tái)、4個(gè)z向振動(dòng)臺(tái)和一個(gè)振動(dòng)臺(tái)面組成[8]。本研究以此系統(tǒng)為研究對(duì)象。

圖2 美國(guó)Hill空軍基地多臺(tái)多軸系統(tǒng)
根據(jù)斯圖爾特平臺(tái)系統(tǒng)的相關(guān)理論,在多軸電動(dòng)振動(dòng)系統(tǒng)中引入類似分析方法,建立如圖3所示的振動(dòng)系統(tǒng)模型。該振動(dòng)系統(tǒng)由振動(dòng)臺(tái)面和8個(gè)獨(dú)立單軸振動(dòng)臺(tái)組成,振動(dòng)臺(tái)用序號(hào)#1,#2,…,#8表示。#1和#2表示x向的振動(dòng)臺(tái),#3和#4表示y向的振動(dòng)臺(tái),#5~#8表示z向的4個(gè)振動(dòng)臺(tái)。為了消除不同軸向運(yùn)動(dòng)之間耦合關(guān)聯(lián),該系統(tǒng)通過連接試驗(yàn)臺(tái)面和振動(dòng)臺(tái)動(dòng)圈的靜壓球形接頭來(lái)實(shí)現(xiàn)機(jī)械解耦。振動(dòng)臺(tái)的下鉸點(diǎn)為具有4個(gè)自由度的球鉸聯(lián)接,固定在系統(tǒng)底座。振動(dòng)臺(tái)的上鉸點(diǎn)與臺(tái)面相連,傳遞作用力。

圖3 八振動(dòng)臺(tái)多軸系統(tǒng)幾何模型
為準(zhǔn)確計(jì)算振動(dòng)臺(tái)的軸向伸縮與臺(tái)面運(yùn)動(dòng)之間的關(guān)系,以#1到#4振動(dòng)臺(tái)與臺(tái)面的連接點(diǎn)所在面的幾何中心為原點(diǎn)建立兩個(gè)空間直角坐標(biāo)系。其中:一個(gè)坐標(biāo)系O-xyz固連于大地,稱為靜坐標(biāo)系S;另一坐標(biāo)系O′-x′y′z′固連于臺(tái)面,稱為動(dòng)坐標(biāo)系M。
8個(gè)振動(dòng)臺(tái)的下鉸點(diǎn)在坐標(biāo)系S中的坐標(biāo)不變,上鉸點(diǎn)在動(dòng)坐標(biāo)系M中的坐標(biāo)不變。臺(tái)面處于中位時(shí)兩坐標(biāo)系重合[9]。原點(diǎn)O到振動(dòng)臺(tái)下鉸點(diǎn)Bi的向量為bi=[bixbiybiz]T,i=1,2,…,8,原點(diǎn)O′到上鉸點(diǎn)Aj的向量為aj=[ajxajyajz]T,j=1,2,…,8。
2 振動(dòng)系統(tǒng)運(yùn)動(dòng)分析
2.1 各振動(dòng)臺(tái)試驗(yàn)?zāi)芰?/h3>
分析各振動(dòng)臺(tái)試驗(yàn)?zāi)芰Γ丛谝阎駝?dòng)臺(tái)面運(yùn)動(dòng)的情況下求得各振動(dòng)臺(tái)軸向的伸縮位移。一般稱此類問題為振動(dòng)系統(tǒng)反解問題。求得各振動(dòng)臺(tái)的軸向伸縮位移,結(jié)合已知振動(dòng)臺(tái)參數(shù),便可判斷振動(dòng)系統(tǒng)的試驗(yàn)?zāi)芰ΑH鐖D3所示,振動(dòng)臺(tái)面的位姿x可以表示為

其中:t3×1為平動(dòng)位移坐標(biāo)向量,即原點(diǎn)O到O′的向量表示為轉(zhuǎn)動(dòng)坐標(biāo)向量分別為繞 x軸、y軸和z軸的轉(zhuǎn)角。
用此3個(gè)參數(shù)可以計(jì)算出靜坐標(biāo)系到動(dòng)坐標(biāo)系的轉(zhuǎn)動(dòng)傳遞矩陣R[15]為

臺(tái)面的運(yùn)動(dòng)速度可以表示為

因?yàn)榕_(tái)面的運(yùn)動(dòng)是8個(gè)振動(dòng)臺(tái)共同激勵(lì)的結(jié)果,下面探求振動(dòng)臺(tái)的軸向伸縮位移與臺(tái)面的位姿之間的關(guān)系。第i個(gè)振動(dòng)臺(tái)上、下鉸點(diǎn)間向量可表示為li,有

其中:li為一個(gè)3×1維的向量,它表示振動(dòng)臺(tái)的位置。

其中:|li|為臺(tái)面運(yùn)動(dòng)時(shí)振動(dòng)臺(tái)的長(zhǎng)度。振動(dòng)臺(tái)的軸向伸縮位移Δli為

其中:li0為無(wú)臺(tái)面運(yùn)動(dòng)時(shí)第i個(gè)振動(dòng)臺(tái)的軸向長(zhǎng)度。
由式(5)可知,振動(dòng)臺(tái)的軸向伸縮位移Δli可以表示成臺(tái)面6個(gè)自由度的函數(shù)。若知振動(dòng)臺(tái)面的運(yùn)動(dòng),可由式(5)求出各振動(dòng)臺(tái)應(yīng)該具備的試驗(yàn)?zāi)芰Α?/p>
2.2 振動(dòng)臺(tái)面極限運(yùn)動(dòng)
振動(dòng)臺(tái)面運(yùn)動(dòng)分析相對(duì)各振動(dòng)臺(tái)軸向位移的求解難度較大,國(guó)內(nèi)外學(xué)者研究了分析振動(dòng)臺(tái)面運(yùn)動(dòng)的方法[18-20]。在實(shí)際工程中僅僅求得振動(dòng)臺(tái)面的運(yùn)動(dòng)是不夠的。振動(dòng)系統(tǒng)的最大試驗(yàn)?zāi)芰υ谡駝?dòng)環(huán)境試驗(yàn)中具有重要的實(shí)際意義,每一個(gè)軸向運(yùn)動(dòng)或轉(zhuǎn)動(dòng)能達(dá)到怎樣的極限位置是值得考慮的問題。
由式(3)和式(5)可以得到一組非線性方程組為

其中:i=128
當(dāng)已知各振動(dòng)臺(tái)的伸縮位移Δli時(shí),式(6)可以寫成
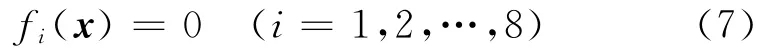
該方程組有8個(gè)方程,6個(gè)未知數(shù)。對(duì)于每組給定的振動(dòng)臺(tái)軸向位移 Δli(i=1,2,…,8),運(yùn)用Newton-Raphson算法或QR分解法都可得到相應(yīng)的臺(tái)面運(yùn)動(dòng)x。每個(gè)振動(dòng)臺(tái)的軸向位移都在一定的范圍內(nèi),即

當(dāng)振動(dòng)臺(tái)軸向位移不同時(shí)臺(tái)面的運(yùn)動(dòng)也不同。分析振動(dòng)臺(tái)面的運(yùn)動(dòng)極限即找出一組最優(yōu)的振動(dòng)臺(tái)軸向位移,使得振動(dòng)臺(tái)面某一自由度的平動(dòng)位移或轉(zhuǎn)角達(dá)到最大值,該值即表示振動(dòng)臺(tái)最大的試驗(yàn)?zāi)芰Α4藭r(shí)可以將振動(dòng)臺(tái)的軸向位移視為自變量,振動(dòng)臺(tái)面的運(yùn)動(dòng)即為軸向位移的函數(shù)。式(7)可以寫為
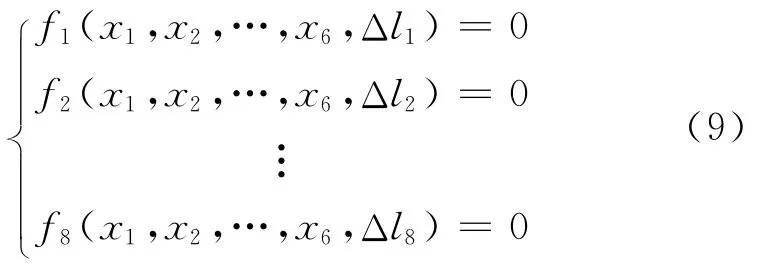
其中:Δli(i=1,2,…,8)為變量,其定義域?yàn)槭剑?)。
臺(tái)面的每個(gè)自由度運(yùn)動(dòng)都可表示為Δli(i=1,2,…,8)的函數(shù),即

3 算 例
3.1 參數(shù)設(shè)定
當(dāng)臺(tái)面運(yùn)動(dòng)時(shí),第i個(gè)振動(dòng)臺(tái)的軸向伸縮位移Δli是以臺(tái)面6個(gè)自由度為自變量的函數(shù)。若是單軸振動(dòng)系統(tǒng),振動(dòng)臺(tái)的伸縮位移即為臺(tái)面的運(yùn)動(dòng)位移。在多軸振動(dòng)系統(tǒng)中,由于不同軸向的振動(dòng)之間存在著機(jī)械耦合,每個(gè)振動(dòng)臺(tái)的運(yùn)動(dòng)不僅產(chǎn)生軸向位移,還對(duì)其他軸向的運(yùn)動(dòng)產(chǎn)生牽連作用,所以當(dāng)單個(gè)振動(dòng)臺(tái)的位移達(dá)到最大值時(shí),試驗(yàn)臺(tái)面的位移并不一定達(dá)到最大值。表1為多軸振動(dòng)系統(tǒng)相關(guān)參數(shù),計(jì)算其臺(tái)面的位移范圍,可以得到上、下各鉸點(diǎn)在靜坐標(biāo)系中的坐標(biāo),如表2和表3所示。

表1 多軸振動(dòng)臺(tái)參數(shù)設(shè)定 mm
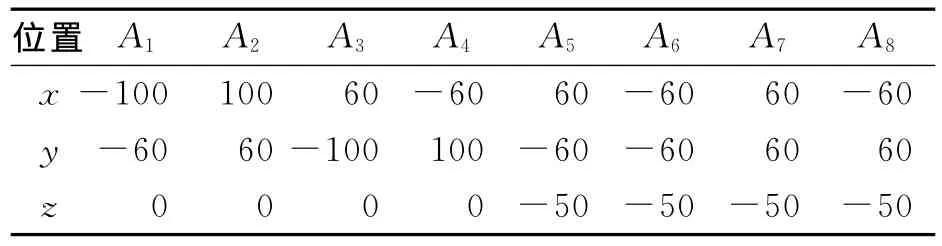
表2 各振動(dòng)臺(tái)上鉸點(diǎn)的坐標(biāo)向量 mm
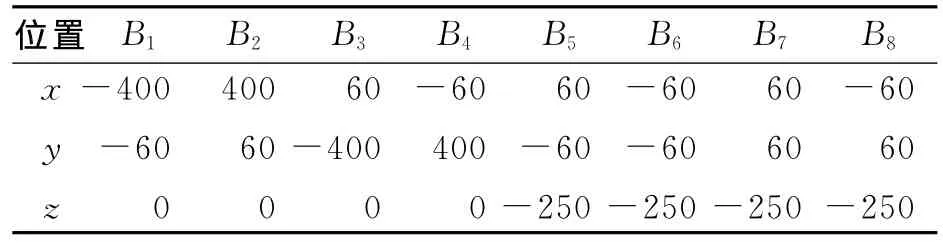
表3 各振動(dòng)臺(tái)下鉸點(diǎn)的坐標(biāo)向量 mm
3.2 計(jì)算結(jié)果
向量aj和向量bi的值分別為Aj和Bi的坐標(biāo)值。可以計(jì)算出振動(dòng)臺(tái)的伸縮位移為何值時(shí)臺(tái)面的位移達(dá)到最大,如表4所示。可以看出,當(dāng)某一軸向振動(dòng)臺(tái)伸縮位移達(dá)到最大值時(shí),該向的臺(tái)面運(yùn)動(dòng)達(dá)到最大值;但臺(tái)面運(yùn)動(dòng)的最大值并不僅由這一軸向的振動(dòng)臺(tái)提供,其他各向振動(dòng)臺(tái)都有位移貢獻(xiàn)。由表4得到該振動(dòng)系統(tǒng)平動(dòng)的運(yùn)動(dòng)范圍為[-25mm,25mm],繞x軸和y軸轉(zhuǎn)動(dòng)角范圍為[-20.805°,20.805°],繞z軸 轉(zhuǎn) 動(dòng) 角 范 圍 為 [-18.168°,18.168°],此為該振動(dòng)系統(tǒng)的試驗(yàn)?zāi)芰Α?/p>
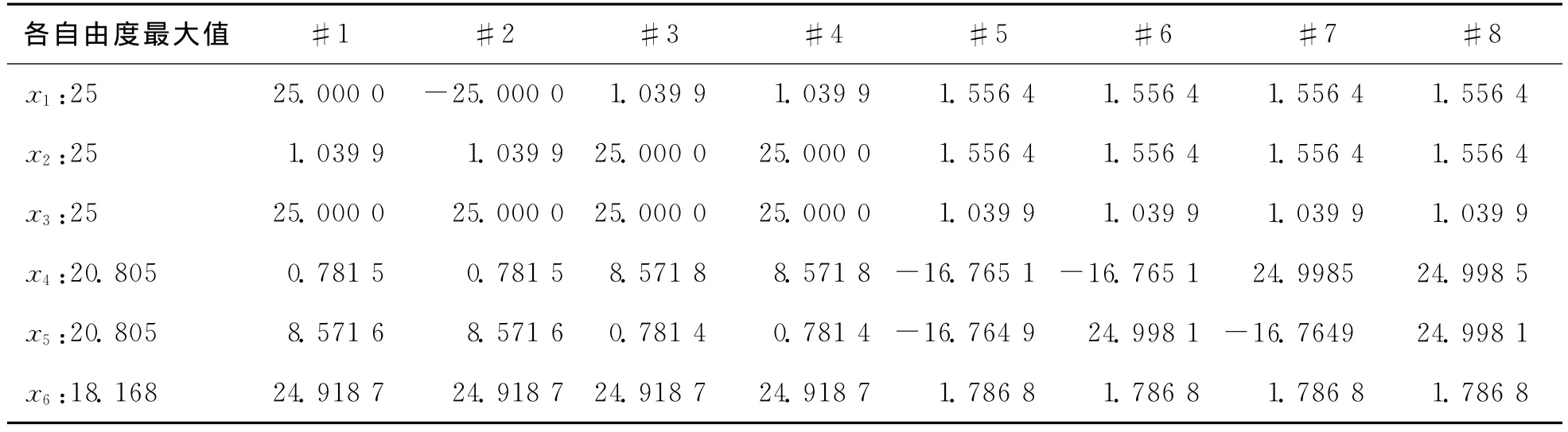
表4 各振動(dòng)臺(tái)位移與臺(tái)面極限位移 mm
另一方面,若已知試驗(yàn)條件,可以求得振動(dòng)臺(tái)應(yīng)具有的試驗(yàn)?zāi)芰Α@纾笈_(tái)面的x軸向位移達(dá)到20mm,同時(shí)繞x軸轉(zhuǎn)動(dòng)角度達(dá)到18°,可以得到各振動(dòng)臺(tái)的軸向位移應(yīng)滿足的條件如表5所示。可以看出,要達(dá)到設(shè)定的試驗(yàn)條件,需要振動(dòng)臺(tái)的最大軸向位移為22.244 0mm,設(shè)計(jì)的振動(dòng)臺(tái)完全能夠滿足此試驗(yàn)要求。
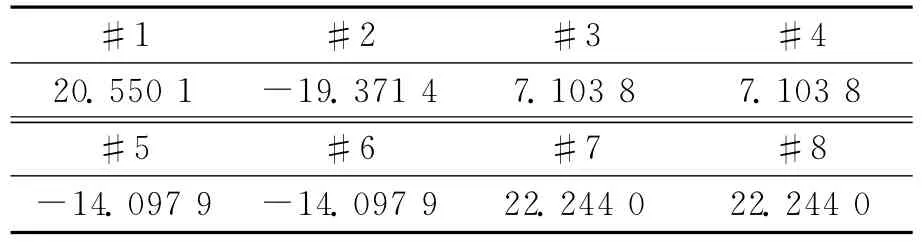
表5 x1=20mm,x4=18°時(shí)各振動(dòng)臺(tái)的軸向位移mm
4 結(jié)束語(yǔ)
在六自由度振動(dòng)試驗(yàn)系統(tǒng)中,不同自由度之間存在機(jī)械耦合,每個(gè)軸向的平動(dòng)或繞軸的轉(zhuǎn)動(dòng)都是由所有振動(dòng)臺(tái)共同作用形成的。筆者在機(jī)械解耦的基礎(chǔ)上計(jì)算試驗(yàn)系統(tǒng)的最大試驗(yàn)?zāi)芰Γ趯?shí)際試驗(yàn)實(shí)施中有著重要的應(yīng)用。筆者僅對(duì)臺(tái)面的位移和振動(dòng)臺(tái)位移之間的關(guān)系進(jìn)行了探討,速度與加速度之間的關(guān)系并未涉及。在多軸振動(dòng)試驗(yàn)中,具有一定質(zhì)量的試件會(huì)對(duì)振動(dòng)臺(tái)產(chǎn)生傾覆力矩,振動(dòng)臺(tái)和臺(tái)面之間的運(yùn)動(dòng)關(guān)系更為復(fù)雜,這些問題需要進(jìn)一步研究。
[1] Davis T.MIMO control system-a new ear in shaker control[J].Sound and Vibration,2006,40(1):6-9.
[2] 夏益霖.多軸振動(dòng)環(huán)境試驗(yàn)的技術(shù)、設(shè)備和應(yīng)用[J].導(dǎo)彈與航天運(yùn)載技術(shù),1996,6:48-55.Xia Yilin.The technology,equipment and application of multi-axis vibration environment testing[J].Missiles and Space Vehicles,1996,6:48-55.(in Chinese)
[3] Harman C.Multi-axis vibration reduces test time[J].Evauluation Engineering,2006,45(6):44-47.
[4] 賀旭東.多輸入多輸出振動(dòng)試驗(yàn)控制系統(tǒng)的理論、算法及實(shí)現(xiàn)[D].南京:南京航空航天大學(xué),2006.
[5] Freeman M T.3-Axis vibration test system simulates real world[J].Test Engineering and Management,1990,12:10-14.
[6] Whiteman W E,Berman M S.Inadequacies in uniaxial stress screen vibration testing[J].Journal of the IEST,2001,44:20-23.
[7] Whiteman W E.Fatigue failure results for multi-axial versus uniaxial stress vibration testing[J].Shock and Vibration,2002,9:319-328.
[8] Chen M,Wilson D R.The new tri-axial shock and vi-bration test system at hill air force base[J].Journal of Institute of Environmental Sciences and Technology,1998,41(2):27-32.
[9] 關(guān)廣豐.液壓驅(qū)動(dòng)六自由度振動(dòng)試驗(yàn)系統(tǒng)控制策略研究[D].哈爾濱:哈爾濱工業(yè)大學(xué),2007.
[10]關(guān)廣豐,王海濤,熊偉.6自由度液壓振動(dòng)臺(tái)運(yùn)動(dòng)學(xué)分析及控制策略[J].振動(dòng)、測(cè)試與診斷,2011,31(1):89-93.Guan Guangfeng,Wang Haitao,Xiong Wei.Kinematic analysis and control strategy of 6-DOF hydraulic vibration table[J].Journal of Vibration,Measurement& Diagnosis,2011,31(1):89-93.(in Chinese)
[11]嚴(yán)俠,牛寶良,朱長(zhǎng)春.三軸六自由度液壓振動(dòng)臺(tái)隨機(jī)振動(dòng)控制分析與仿真[J].機(jī)床與液壓,2007,35(10):165-191.Yan Xia,Niu Baoliang,Zhu Changchun.MIMO random vibration control simulation in the three axis-six DOF shaking table[J].Machine Tool & Hydraulics,2007,35(10):165-191.(in Chinese)
[12]陳建秋.六自由度模擬地震振動(dòng)臺(tái)臺(tái)面控制原理研究[J].廣州大學(xué)學(xué)報(bào):自然科學(xué)版,2006,5(3):75-79.Chen Jianqiu.Analysis of 6-DOF and table control of seismic simulation system[J].Journal of Guangzhou University:Natural Science Edition,2006,5(3):75-79.(in Chinese)
[13]陳建秋,任珉,楊澤群.模擬地震振動(dòng)臺(tái)臺(tái)面補(bǔ)償技術(shù)分析[J].廣州大學(xué)學(xué)報(bào):自然科學(xué)版,2005,4(1):74-77.Chen Jianqiu,Ren Min,Yang Zequn.Analysis of compensation technology of seismic simulation system[J].Journal of Guangzhou University:Natural Science Edition,2005,4(1):74-77.(in Chinese)
[14]Koebebakker S.Model based control of a flight simulator motion system[D].Delft:Delft University of Technology,2001.
[15]馬建明.飛行器模擬液壓Stewart平臺(tái)奇異位形分析及其解決方法研究[D].哈爾濱:哈爾濱工業(yè)大學(xué),2010.
[16]Bhaskar D,Mruthyunjaya T S.The stewart platform manipulator:a review[J].Mechanism and Machine Theory,2000(35):15-40.
[17]Underwood M A,Keller T.Applying coordinate transfor-mations to multi-DOF shaker control[J].Sound and Vibration,2006,1:2-8.
[18]Lin W,Griffis M,Duffy J.Forward displacement analysis of the 4-4stewart platforms[J].Journal of Mechanical Design,1992,114:444-450.
[19]Raghavan M.The stewart platform of general geometry has 40configurations[J].Journal of Mechanical Design,1993,115(2):277-282.
[20]Ku D M.Direct displacement analysis of a stewart platform mechanism [J]. Mechanism and Machine Theory,1999,34:453-465.

