基于Lagrangian Gaussian光束的數值方法
高景璐,郝永樂,孟品超
(1.吉林大學 數學學院,長春 130012;2.長春理工大學 理學院,長春 130022)
1 基于Green函數的Gaussian光束
在地震波模擬和高頻狀態遷移中,Gaussian光束累加方法應用廣泛[1-10].對于標量波場U(x,ω),考慮如下Helmholtz波動方程:
2U(x,ω)+ω2n2(x)U(x,ω)=-δ(x-xe),
(1)
其中:x∈d(d=2,3);ω為頻率;n(x)表示在x點的波速;xe為源點坐標.
對于U(x,ω),用標準幾何光學高頻率(即ω較大)擬設:
U(x,ω)=[A(x)+O(1/ω)]exp{iωτ(x)}.
(2)
將式(2)代入式(1),并令ω-2和ω-1為0,可得關于傳播時間τ和振幅A且有相應初始條件的程函方程和遷移方程:
(τ)2=n2,
(3)
(4)
當ω足夠大時,可以視Hellmholtz算子為橢圓型微分算子:
(5)
其中:p=(p1,p2,…,pn);x=(x1,x2,…,xn).
對于給定的光線γ,可以用文獻[11-12]中的梁理論構建Gaussian射束,假設γ(s)={x(s)=x(s;xe,pe)},可得{p(s;xe,pe)}=τ(x(s)).對于如下射線追蹤系統:
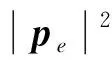
由梁理論[11-12],2τ的Hessian陣滿足如下Riccati方程:
(10)
其中:
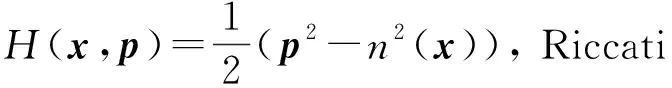
(11)
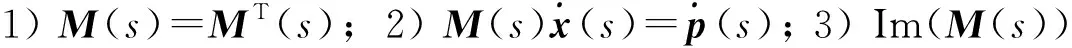
下面用遷移方程(4)得到光線上的振幅函數.由
方程(4)可寫成
(12)
由方程(4)和上述結果可見,振幅永遠不會無窮大,因此它也不會發散.
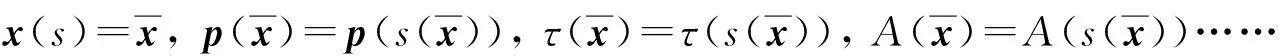
(13)
即定義了相位函數的一個全局逼近.類似地,可以定義O中沿中心線的振幅:
(14)
因此,單一光束的解可定義為
u(x;xe,pe)=A(x;xe,pe)exp{iωτ(x;xe,pe)}.
(15)
先對Helmholtz方程用Green函數,再對pe進行疊加,得
(16)
其中α(ω)為響應的某個常數[13].
2 2D波動方程的實現
下面考慮2D Helmholtz波動方程Lagrangian Gaussian光束的實現(d=2,x=(x,y),xe=(xe,ye)):
2U(x,y,ω)+ω2n2(x,y)U(x,y,ω) =-δ(x-xe)δ(y-ye),
(17)

2.1 預處理階段
對于程函方程(3),取p=(p1,p2)=(ncosθ,nsinθ)(用θ代替p1,p2),通過式(6)~(9),射線追蹤系統可化為
(18)
其中φe∈[0,2π]為相應于pe=((p1)e,(p2)e)的θ的初值.
進而,Riccati方程可化為
(19)
其中
D=-n2n-n·
為了保證非線性Riccati方程[12]有全局解,需對Hessian陣M(0)做如下約束:
1)M(0)=MT(0);
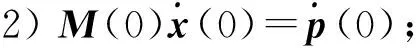

取
易見M(0)滿足條件1);由條件2)等價于
(20)
選取
(21)
則其實數部分也滿足條件2);對于條件3),有
a2sin2φe-2b2sinφecosφe+c2cos2φe≥0,
(22)
若取
(a2,b2,c2)=(sin2φe,-sinφecosφe,cos2φe),
(23)
則方程(22)和(20)的第二部分都成立.
從而遷移方程可寫成:
(24)
預處理階段步驟如下:
1) 離散計算區域,指標xi,yj,φm,sn分別為:
當n=1時初始化所有函數:
xs(n,m)=xe,ys(n,m)=ye,θ(n,m)=φm,τ(n,m)=0,A(n,m)=1,
其中xs(n,m)和ys(n,m)是光線上點的坐標.M(n,m)的初始值在式(21),(23)中都有說明.
2) 求解Liouville方程(18),(24).對于每個m=1,2,…,Nφ和n=1,2,…,Ns,定義xs(n,m),ys(n,m),θ(n,m),τ(n,m),M(n,m),A(n,m).
2.2 后置處理階段
Lagrangian Gaussion光束(LGB)的計算效率由兩部分組成:
1) 對于一個給定的光線,需找到一個合適的鄰域,使得其滿足對鄰域中每個點得到的振幅無限小;
2) 對于1)中找到的給定點的鄰域,需要在過其光線上找到離其最近的一個點.
對于1),文獻[5]已給出了很多方法,本文給出一個更有效的新方法.圖1顯示了在光線的鄰域內,只有一個集中域存在明顯的振幅.表明要得到一個Gaussian射束,不需要計算所有的網格點.
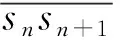
(25)
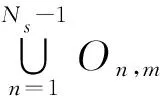
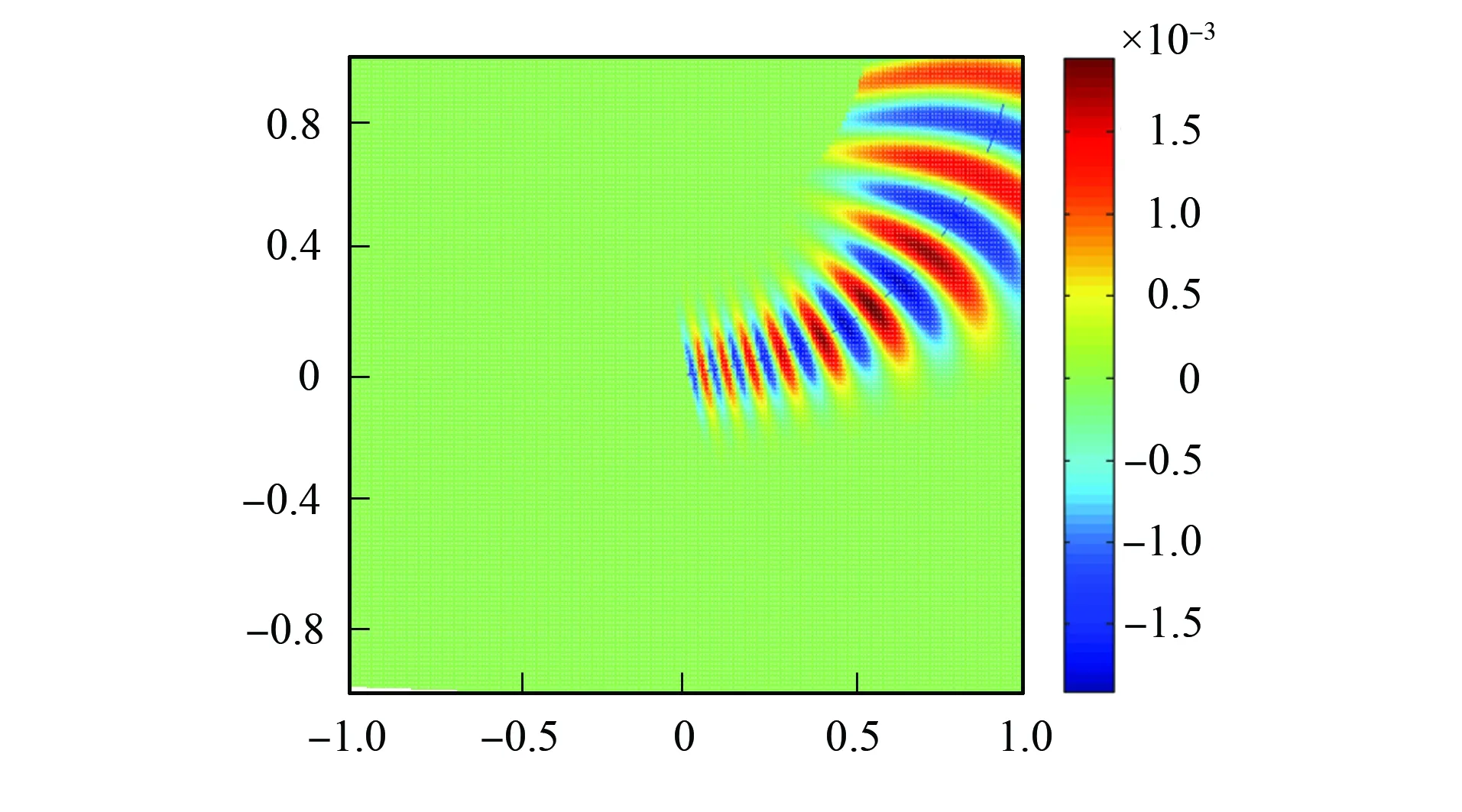
圖1 波導管Gaussian射束Fig.1 Waveguide Gaussian beam
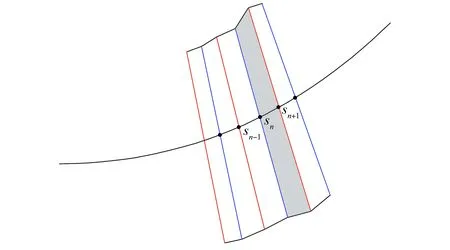
圖2 一小段光線γ的鄰域Fig.2 Neighborhood of a segment of ray γ

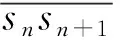
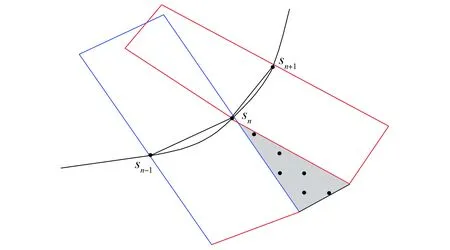
圖方法射線γ的鄰域Fig.3 Neighborhood of ray γ method
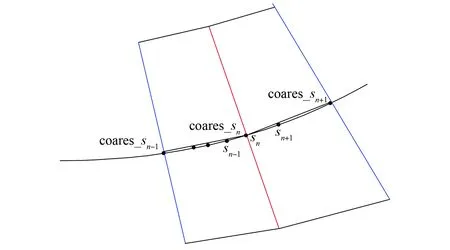
圖4 分割粗糙時射線γ的鄰域Fig.4 Neighborhood of ray γ under coarse segmentation
下面討論鄰域的遍歷方法,不失一般性,考慮射線γ斜率小于1的情況.
2.2.1 區域On,m的遍歷算法
2) 對每個當前點yj,用y=yj分割clsn-1和clsn可得min_x和max_x,然后遍歷xi從min_x到max_x.
2.2.2 尋找最近點的算法
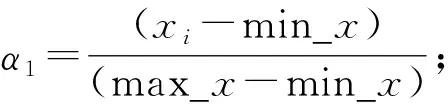
2) 在當前區域On,m,已知csn-1和csn,運用插值公式
s(xi,yj)=csn-1+α1(csn-csn-1)
可以求出s(xi,yj),則對應于s(xi,yj)的點即為要尋找的點.
注3由于Δs相對于網格上的點較小,取coarse_N作為Δcs,同時要求Δcs的兩個端點斜率相差不大(以coarse_N=10為例).在上述條件下,On,m即可視為一個矩形.根據該算法,只需要計算α1和s(xi,yj),避免了局域性的搜索,如圖6所示.
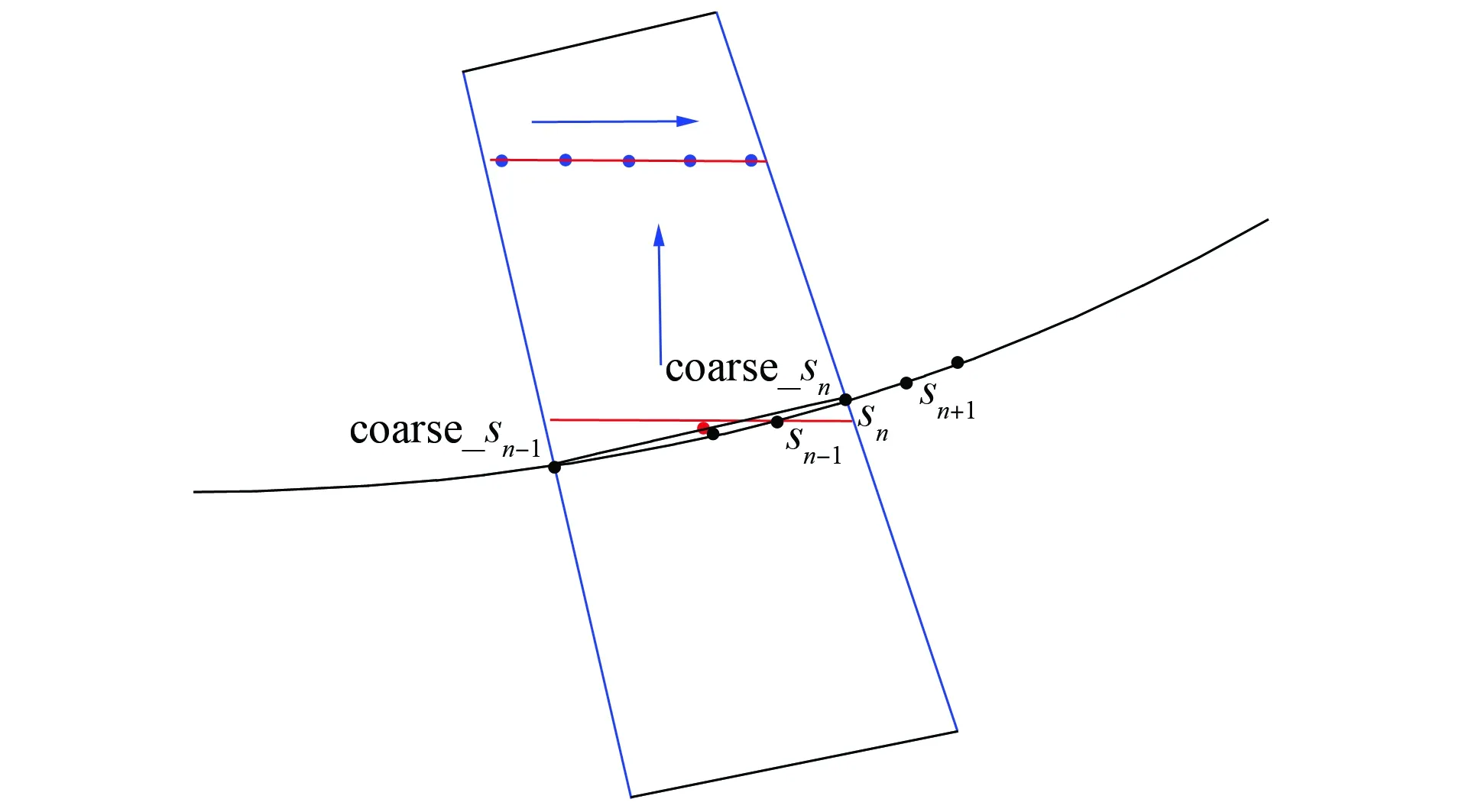
圖5 鄰域的遍歷算法Fig.5 Neighborhood traversal algorithms
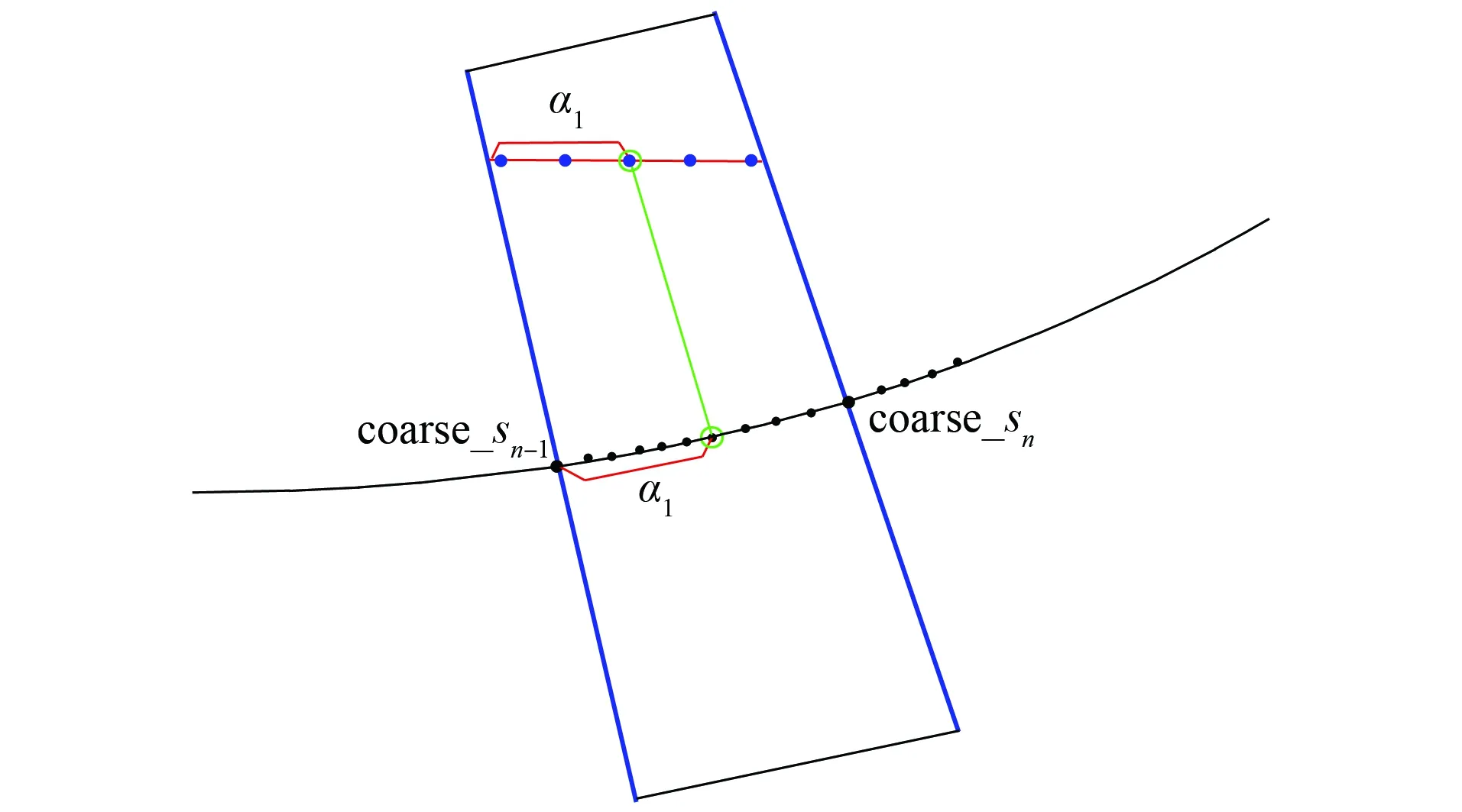
圖6 在γ上尋找最近點的方法Fig.6 Finding the nearest point on γ
2.2.3 后置處理過程
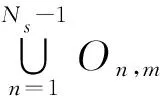
2) 對于(xi,yj),找到γm上關于s(xi,yj)的最近點;
3) 對于固定的點(xi,yj)和對應γm上的最近點,用式(13)~(15)得到一個Gaussian射束;
4) 將所有的Gaussian射束組合即構成一個完整的波域.
3 數值實例
3.1 常值模型
當v(x,y)=1時,漸近射線理論(ART)的解即為Hankel方程的漸近展開,它也是一點處Hankel方程的精確解.可以用這個解檢驗Eulerian Gaussian射束Eulerian凍結Gaussian射束的數值解.下面用這兩種方法考察ω=16π時的情況.
3.2 波導模型
當速度函數為v(x,y)=3-2.5exp{-2x2}時,射線追蹤顯示在逼近源位置上該模型會發生焦散.傳統的射線理論和Gaussian光束理論都預測了在焦散處有無窮次震動.因此可以用該模型檢驗Gaussian光束理論的正確性.
圖7和圖8分別為常值模型和波導模型的射線;圖9和圖10分別為ω=16π時常值模型和波導模型的數值結果.
圖7 源為(xe,ye)=(0,0)時常值模型的射線Fig.7 Ray of constant model at source (xe,ye)=(0,0)

圖8 源為(xe,ye)=(0,0)時波導模型的射線Fig.8 Ray of waveguide model at source (xe,ye)=(0,0)
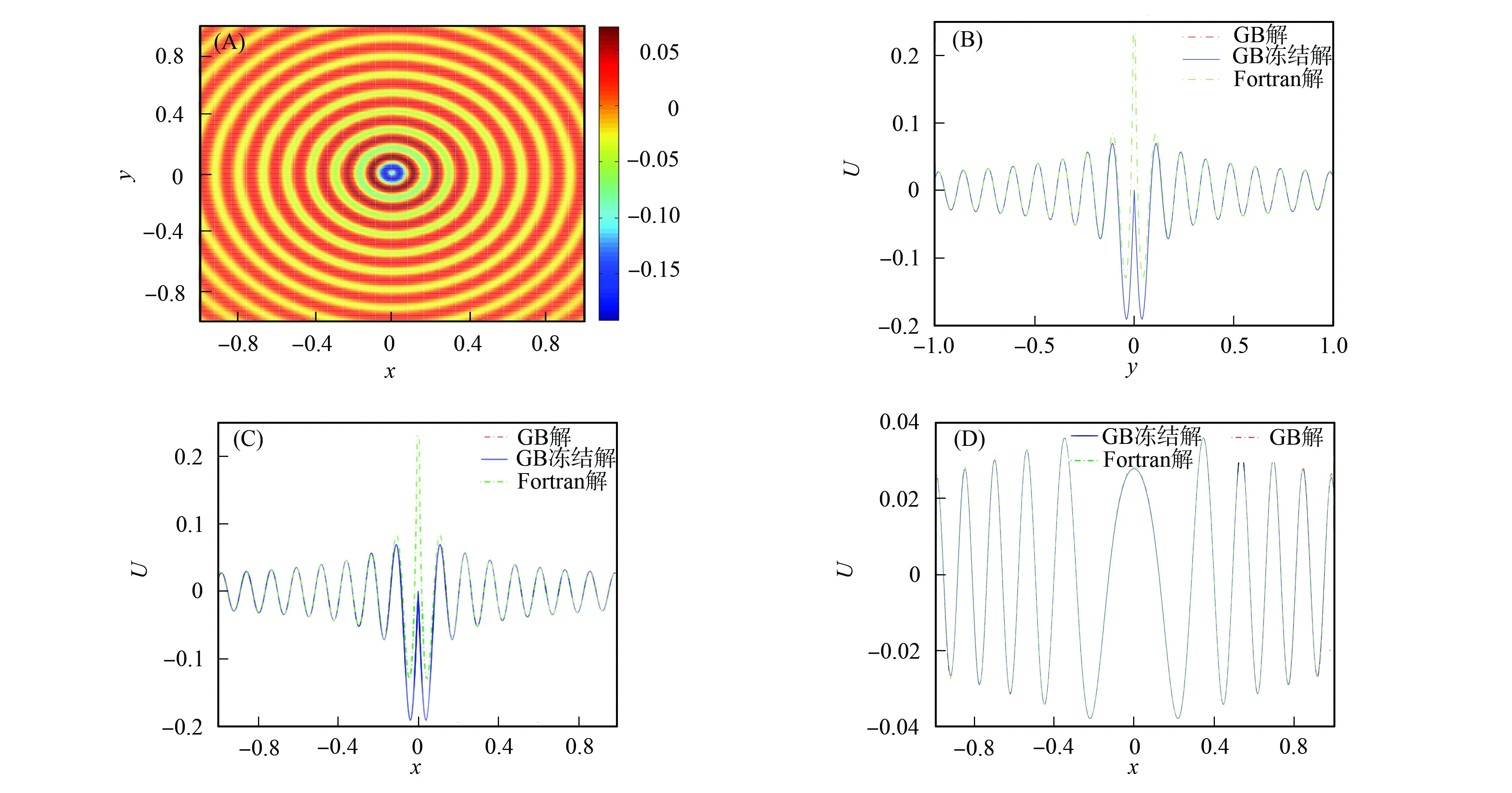
(A) 真正的波場部分;(B) 在x=0處的切片;(C) 在y=0處的切片;(D) 在y=0.5處的切片.圖9 ω=16π時常值模型的數值結果Fig.9 Numerical results for constant model when ω=16π

(A) 真正的波場部分;(B) 在x=0處的切片;(C) 在y=0處的切片;(D) 在y=0.5處的切片.圖10 ω=16π時波導模型的數值結果Fig.10 Numerical results for waveguide model when ω=16π
[1] Alkhalifah T.Gaussian Beam Depth Migration for Anisotropic Media [J].Geophysics,1995,60(5):1474-1484.
[2] Babich V M,Buldyrev V S.Asymptotic Methods in Short-Wave Length Diffraction Problems [M].Moscow:Nauka,1972.
[4] Gray S.Gaussian Beam Migration of Common Shot Records [J].Geophysics,2005,70:133-136.
[5] Hill N R.Gaussian Beam Migration [J].Geophysics,1990,55(11):1416-1428.
[6] Hill N.Prestack Gaussian-Beam Depth Migration [J].Geophysics,2001,66:1240-1250.
[7] Norris A V,White B S,Schrieffer J R.Gaussian Wave Packets in Inhomogeneous Media with Curved Interfaces [J].Proc Roy Soc London,Ser:A,1987,412:93-123.
[8] White B S,Norris A N,Bayliss A,et al.Some Remarks on the Gaussian Beam Summation Method [J].Geophysical Journal of the Royal Astronomical Society,1987,89(2):579-636.
[9] LUO Song-ting,QIAN Jian-liang.Factored Singularities and High-Order Lax-Friedrichs Sweeping Schemes for Point-Source Traveltimes and Amplitudes [J].J Comput Phys,2011,230(12):4742-4755.
[10] LEUNG Shing-yu,QIAN Jian-liang.The Backward Phase Flow and FBI-Transform-Based Eulerian Gaussian Beams for the Schr?dinger Equation [J].J Comput Phys,2010,229(23):8888-8917.
[11] Ralston J.Gaussian Beams and the Propagation of Singularities,Studies in Partial Differential Equations [J].MAA Studies in Mathematics,1982,23:206-248.
[12] Tanushev N M,QIAN Jian-liang,Ralston J.Mountain Waves and Gaussian Beams [J].Multiscale Model Simul,2007,6(2):688-709.
[13] LEUNG Shing-yu,QIAN Jian-liang,Burridge R.Eulerian Gaussian Beams for High Frequency Wave Propagation [J].Geophysics,2007,72(5):61-76.

