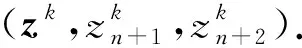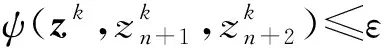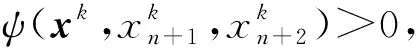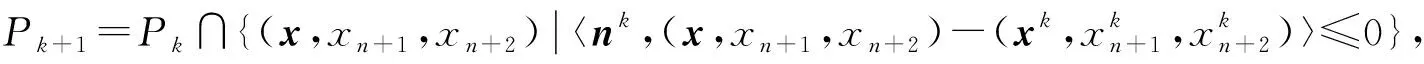求解一般D.C.規劃的全局最優解
徐俊彥,苗 壯,劉慶懷
(長春工業大學 基礎科學學院,長春 130012)
0 引言與預備知識
考慮優化問題:
(1)
其中:f(x),gi(x)(i=1,2,….m):n→,并且有二階連續偏導數.
通常用求解問題(1)的外逼近或分支定界算法求出一個不可行的解序列xk,使得xk→x*(k→∞),x*為最優解,而f(xk)→f*(k→∞),f*為最優值.但在實際應用中,算法必須在有限步內終止于某個xk,將xk作為x*的近似值,此時的xk可能是不可行的,甚至遠離真正的最優解.為了克服這些問題,文獻[1-7]提出了非孤立最優解的概念.本文將其推廣到一般D.C.優化問題中.
引理1[8]二階偏導數處處連續的函數是D.C.函數.
引理2[8]對于集合
M={(x,xn+1)∈n+1|di(x,xn+1)≤0(i=1,2,…,m)},
存在一個D.C.集:
F={(x,xn+1,xn+2)∈n+2|φ(x,xn+1,xn+2)≤0,ψ(x,xn+1,xn+2)≥0},
使得
(x,xn+1,xn+2)∈F? (x,xn+1)∈M,
其中:di(x,xn+1)(i=1,2,…,m)為D.C.函數;φ(x,xn+1,xn+2)和ψ(x,xn+1,xn+2)是凸函數.
1 問題(1)的等價轉化
由引理1可知,問題(1)中的函數是D.C.函數,該問題為一般D.C.規劃.問題(1)等價于:
(2)
記
M={(x,xn+1)∈n+1|gi(x)≤0,f(x)-xn+1,i=1,2,…,m},
d(x,xn+1)=max{gi(x),f(x)-xn+1,i=1,2,…,m}.
根據D.C.函數的性質,d(x,xn+1)是D.C.函數.
設d(x,xn+1)=p(x,xn+1)-q(x,xn+1),p,q均為凸函數,則
M={(x,xn+1)∈n+1|d(x,xn+1)≤0}.
令
φ(x,xn+1,xn+2)=p(x,xn+1)-xn+2,ψ(x,xn+1,xn+2)=q(x,xn+1)-xn+2.
顯然φ,ψ都是凸函數.
記
F={(x,xn+1,xn+2)∈n+2|φ(x,xn+1,xn+2)≤0,ψ(x,xn+1,xn+2)≥0},
(3)
則由引理2知,問題(2)等價于:
min{xn+1|(x,xn+1,xn+2)∈F},
(4)
其中F由式(3)定義.易見問題(4)是典范D.C.規劃.
因此,求解問題(1)的最優解等價于求解一個典范D.C.規劃的最優解.記D={(x,xn+1,xn+2)∈n+2|φ(x,xn+1,xn+2)≤0},則D為凸集.問題(4)可寫為
min{xn+1|(x,xn+1,xn+2)∈D,ψ(x,xn+1,xn+2)≥0}.
(5)
2 主要結果
在實際應用中,孤立最優解是不可用的,因為孤立最優解極不穩定,當約束條件稍有擾動時,孤立最優解就可能是不可行的.因此非孤立最優解更有應用價值.
假設:
(H1)D={(x,xn+1,xn+2)∈n+2|φ(x,xn+1,xn+2)≤0}是緊集,并且intD≠?;
(H2) 存在滿足ψ(a,an+1,an+2)<0和an+1 (H3)F=cl intF,其中F由式(3)定義; (H4) {(x,xn+1,xn+2)∈D|xn+1≤γ}=cl{(x,xn+1,xn+2)∈intD|xn+1≤γ},γ∈; (H5) 存在(ω,ωn+1,ωn+2)∈n+2,使得對任意的(x,xn+1,xn+2)∈D,有ωn+1-ε>xn+1成立. 如果(x,xn+1,xn+2)為問題(5)的可行解,存在點(x,xn+1,xn+2)的某個領域,使得在該領域內除點(x,xn+1,xn+2)外,其他點均為不可行的,則稱點(x,xn+1,xn+2)為問題(5)的孤立可行解.若最優解在孤立可行解處得到,則稱其為孤立最優解. 其中 s*=cl{(x,xn+1,xn+2)|(x,xn+1,xn+2)∈intD,ψ(x,xn+1,xn+2)>0}, 設 {(x,xn+1,xn+2)∈n+2|(x,xn+1,xn+2)∈intD,ψ(x,xn+1,xn+2)>0}≠?. 對于給定的ε≥0,若 (x,xn+1,xn+2)∈{(x,xn+1,xn+2)∈n+2|(x,xn+1,xn+2)∈D,ψ(x,xn+1,xn+2)>ε}, 則稱問題(5)是正則的. 考慮如下輔助問題(p/γ): max{ψ(x,xn+1,xn+2)|(x,xn+1,xn+2)∈D,xn+1≤γ,γ∈}. 由于函數ψ(x,xn+1,xn+2)連續,所以在條件(H4)成立時,問題(p/γ)是正則的.下面證明當條件(H4)成立時,求問題(5)的ε-非孤立最優解等價于求問題(p/γ)的最優解. 令min(問題(5))和max(p/γ)分別表示問題(5)和問題(p/γ)的最優值. 定理1設條件(H4) 成立. {(x,xn+1,xn+2)∈n+2|(x,xn+1,xn+2)∈D,ψ(x,xn+1,xn+2)≥ε}=?. 因而,對使得ψ(x,xn+1,xn+2)>ε的每個(x,xn+1,xn+2)∈D,都有xn+1≥γ成立,即 (6) {(x,xn+1,xn+2)∈n+2|(x,xn+1,xn+2)∈D,ψ(x,xn+1,xn+2)≥ε}=?, 即問題(5)沒有ε-非孤立可行解. 算法1在假設(H1)~(H5)成立的條件下,算法步驟如下: 3) 計算 5) 若xn+1-γ=0,則令nk=(0,…,0,1,0)∈n+2;若則令 定理2算法1在有限步迭代后終止,或產生問題(5)的一個ε-非孤立最優解或證明問題(5)沒有ε-非孤立可行解. 例1 其輔助問題(p/γ)為 當ε=0.000 1時,計算所得數值結果列于表1,其最優解為(6.000 1,0.764 0),最優值為-3.127 4. 表1 例1的計算結果Table 1 Computational results of example 1 例2 其輔助問題(p/γ)為 當ε=0.000 1時,計算所得數值結果列于表2,其最優解為(-0.988 6,3.100 1),最優值為57.325 7. 表2 例2的計算結果Table 2 Computational results of example 2 由表1和表2可見,算法1是有效的,收斂于非孤立全局最優解. [1] Tuy H.Robust Solution of Non-convex Global Optimization Problems [J].J Glob Optim,2005,32(2):307-323. [2] Tuy H.Polynomial Optimization:A Robust Approach [J].Pac J Optim,2005,1:357-374. [3] Tuy H,Hoai Phuong.A Robust Algorithm for Quadratic Optimization under Quadratic Constraints [J].J Glob Optim,2007,37(4):557-569. [4] SHEN Pei-ping,MA Yuan,CHEN Yong-qiang.A Robust Algorithm for Generalized Geometric Programming [J].J Glob Optim,2008,41(4):593-612. [5] Tuy H.D(c)-Optimization and Robust Global Optimization [J].J Glob Optim,2010,47(3):485-501. [6] SHEN Pei-ping,MA Yuan,CHEN Yong-qiang.Global Optimization for the Generalized Polynomial Sum of Ratios Problem [J].J Glob Optim,2011,50(3):439-455. [7] Tuy H,Thach P T,Konno H.Optimization of Polynomial Fractional Functions [J].J Glob Optim,2004,29(1):19-44. [8] Horst R,Pardalos P M,Thoai N M.Introduction to Global Optimization [M].Dordrecht:Kluwer Academic Publishers,2000.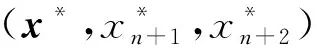
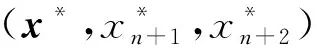


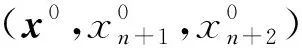

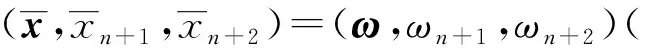
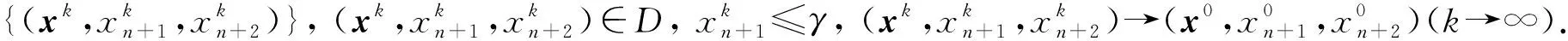
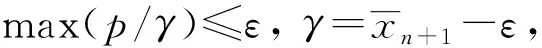

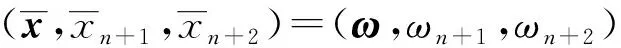
3 算法及數值實例