基于公路工程技術標準的載重貨車動荷載系數研究

胡 朋 ，劉 波

(1.山東交通學院 土木工程學院，山東 濟南 250357； 2.山東大學 土建與水利學院，山東 濟南 250061)

路面不平度的隨機激勵會加劇行駛車輛的振動，影響汽車平順性、動力性、經濟性和行駛安全性，形成動荷載，從而加劇路面破壞。對路面不平度的深入研究是開展汽車-道路相互作用研究這個新領域必不可少的一環，也是路-車-人相互作用研究以及汽車地面力學研究的基本內容[1-7]。多位學者進行過動荷載系數的研究[1-3]，但幾乎都是以路面功率譜密度作為路面平整度技術標準，未考慮公路路面平整度的實際標準。

本文以公路工程技術標準中平整度要求為切入點，分析公路工程技術標準中平整度和路面功率譜密度的關系；以傅里葉變換為求解方法，推導五自由度車輛振動模型動荷載系數計算公式，在此基礎上計算五自由度車輛振動模型典型載重貨車的前后輪動荷載系數。

1 路面不平度指標的分類及關系

道路平整度是指路面表面相對于理想平面的豎向偏差，這種偏差會影響到車輛動力特性、行駛質量、路面所受動荷載。國際平整度指數IRI、連續平整度儀測定的標準差σ和路面功率譜密度PSD是評價路面平整度的三大指標，前兩者對應于道路工程，后者在車輛學科中研究較多。

1.1 路面不平度功率譜密度

根據文獻[8]，路面不平度功率譜密度的擬合表達式為

式中n為空間頻率，是波長λ的倒數，表示每m中包含波的數量。n0為參考空間頻率，取0.1 m-1；Gq(n0)為參考空間頻率n0下的路面功率譜密度，取決于路面等級，見表1，在此僅列出A、B、C 3個等級；ω為頻率指數，為雙對數坐標上斜線的斜率，它決定路面功率譜密度的頻率結構，在路面分級時取ω=2。

1.2 公路工程平整度要求

文獻[9]規定新建高速公路和一級公路平整度應滿足IRI<2.0 m/km，σ<1.0；文獻[10]規定新建高速公路和一級公路上面層平整度應滿足σ<1.2，其它公路σ<2.5；文獻[11]規定新建高速公路和一級公路平整度應滿足IRI<2.0 m/km，σ<1.2，其它公路IRI<3.2 m/km，σ<2.0。

1.3 平整度指標之間的關系

表1 路面不平度分類標準

平整度指標IRI、σ和PSD之間的關系[12-15]為

以此作為標準，結合規范規定，取高速公路和一級公路的路面功率譜密度Sq(n0)=11, 其它公路Sq(n0)=28。

2 五自由度車輛振動模型及動荷載計算

圖1 五自由度車輛振動模型

車輛動荷載的計算一般都是將車輛簡化為多自由度振動模型[3-6]，然后求解。自由度越多，求解越困難，但自由度過少會導致計算結果和實際偏離太遠。本文采用五自由度車輛模型進行求解。

2.1 五自由度車輛振動模型

對于雙軸汽車，由于左右對稱，故取其一半，并考慮車輛縱向的傾覆和轉動，將車輛簡化為如圖1所示的五自由度車輛振動模型，并假定彈簧剛度系數和阻尼系數均為線性系數。圖中各參數的意義如表2所示。

該車輛模型懸架在ks和Cs處m的位移為y-aφ；在kf和Cf處的位移為y-dφ； 在kr和Cr處的位移為

y+bφ。

表2 五自由度車輛模型參數意義

ms的振動方程為

(1)

mtf的振動方程為

(2)

mtr的振動方程為

(3)

m的垂向振動方程為

(4)

M的轉動方程為

(5)

2.2 五自由度車輛振動模型幅頻特性求解

對式(1)～(5)進行傅里葉變換，得到

(6)

(7)

(8)

(9)

(10)

MY=X，

(11)

由于模型為1/2車輛模型，設前后軸距為L，則后輪行駛軌跡和前輪一致，只是存在滯后時間Δt=L/v，因而前后輪行駛的路面不平度功率譜密度在相位上滯后ωΔt。

MH=X1，

(12)

2.3 五自由度振動模型前后輪動荷載系數求解

(13)

為了求出動荷載系數對路面不平度激勵的頻響函數，將式(13)進行傅里葉變換，得到

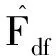
則前輪動荷載系數對路面不平度激勵的頻響函數H(ω)DLCf-x為

動荷載系數的功率譜密度[16]GDLCf/G(f)為

GDLCf/G(f)=|H(ω)DLCf-x|2Gx(f).

(14)

同理，后輪動荷載為Fdr

進行傅里葉變換，得

則后輪動荷載系數對路面不平整度激勵的頻響函數H(ω)DLCr-x為

求得動荷載系數的功率譜密度為

GDLCr/G(f)=|H(ω)DLCr-x|2Gx(f).

(15)

從統計意義上來講，車輛動荷載正負的機率相等，動荷載的均值為0，動荷載系數的均值也為0，其方差就等于均方值

(16)

將式(14)和(15)代入式(16)，就可以得到前后輪動荷載系數的方差，即均方值，從而求得動荷載系數均值。

式(16)中的幅頻特性表達式非常復雜，無法用解析的方法進行積分。本文采用MATLAB進行數值求解。

3 計算實例

某種重型貨車的各參數[17]分別為：車輛座椅及駕駛員質量的一半ms=100kg，前輪胎質量mtf=480kg，后輪胎質量mtr=945 kg，車架和裝載物質量和m=7 885 kg，車架繞質心的轉動慣量J=37 432kg·m，座椅剛度系數ks=2.1 kN/m，前懸掛剛度系數kf=150 kN/m，前輪胎剛度系數ktf=2.8MN/m，后懸掛剛度系數kr=370kN/m，后輪胎剛度系數ktr=8.9MN/m，座椅阻尼系數Cs=1.8kN·s/m，前懸掛阻尼系數Cf=7kN·s/m，前輪胎阻尼系數Ctf=2kN·s/m，后懸掛阻尼系數Cr=14kN·s/m，后輪胎阻尼系數Ctr=3kN·s/m。

座椅中心至車架質心的距離a=0.5m，后輪中心至車架質心的距離b=3.1m，前輪中心至車架質心的距離d=2.5m，前后輪中心距離L=b+d，則前后輪駛過同一地點的時間差為Δt=L/v。

經過程序計算，得到高速公路和一級公路、其它等級公路的路面和不同車速下的前后輪動荷載系數功率譜密度和激振頻率f之間的關系。

以平整度等級為高速和一級公路，車輛行駛速度80km/h為例，前后輪動荷載系數功率譜密度和激振頻率f之間的關系如圖2、3所示。

圖2 前輪動荷載系數功率譜密度和激振頻率f之間的關系 圖3 后輪動荷載系數功率譜密度和激振頻率f之間的關系

路面平整度等級車輛速度/(km·h-1)前輪動荷載系數后輪動荷載系數高速公路和一級公路1200.129 00.105 51000.115 60.106 6800.106 30.091 7其它公路800.169 60.114 0600.146 00.085 0400.118 50.082 1

從圖2、3可以看出，前輪和后輪都在約1Hz和5Hz左右出現共振現象，但前輪在1Hz左右共振明顯，后輪在5Hz左右共振明顯。

因四級公路車輛較少，車速較慢，所以在此不再計算30km/h和20km/h情況下的動荷載系數。

其它不同速度和不同平整度等級路面的動荷載系數如表3所示。

從表3可以看出，動荷載系數均值隨著路面平整度等級的降低而增大,隨著車速的提高而增大。前輪的動荷載系數比后輪略大，這主要是由質心位置靠前、前后輪胎的剛度不同導致的。

4 結論

利用傅里葉變換推導出了五自由度車輛振動模型在路面不平度激勵下的動荷載系數的計算公式，并編制了相應的MATLAB計算程序。

五自由度貨車模型的計算結果表明，當以公路工程技術標準規定的路面平整度技術指標作為路面平整度條件時，動荷載系數大約在10%左右；動荷載系數均值隨路面平整度等級的降低而顯著增大，隨車速的提高而增大；前輪動荷載系數大于后輪動荷載系數。

參考文獻：

[1]鐘陽，王哲人，張肖寧.不平整路面上行駛的車輛對路面隨機動壓力的分析[J].中國公路學報，1992,5(2)：41-43.

[2]孫璐,鄧學均. 車輛-路面相互作用產生的動力荷載[J].東南大學學報, 1996, 26(5): 142-145.

[3]鄭京杰，李躍軍. 汽車對路面作用的隨機動荷載分析[J].中南公路工程，1999，24(1):8-10.

[4]鄧學鈞.車輛地面結構系統動力學研究[J].東南大學學報:自然科學版,2002,32(3)：474-479.

[5]郭成超,陶向華,王復明.車速和路面不平度特性對車路相互作用的影響[J].華北水利水電學院學報,2004,25(3):42-45.

[6]張洪亮，胡長順.基于五自由度車輛模型的橋頭搭板容許縱坡變化值研究[J].土木工程學報，2005，38(6):125-130.

[7]胡朋，張婧竼，張建娟.基于快速傅里葉逆變換的路面平整度仿真分析[J].山東交通學院學報，2009，17(3)：44-47.

[8]中國工業機械聯合會.GB/T7031—2005 機械振動道路路面譜測量數據報告[S]．北京：中國標準出版社，2005.

[9]中交公路規劃設計院.JTGD50—2006 公路瀝青路面設計規范[S].北京：人民交通出版社，2006.

[10]交通部公路科學研究所.JTGF40—2004 公路瀝青路面施工技術規范[S].北京：人民交通出版社，2005.

[11]交通部公路科學研究所.JTGF30—2003 公路水泥混凝土路面施工技術規范[S].北京：人民交通出版社，2003.

[12]周曉青,孫立軍.國際平整度指數與行駛車速的關系[J].同濟大學學報：自然科學版,2005,33(10):1323-1327.

[13]吳慶雄,陳寶春,奚靈智.路面平整度PSD和IRI評價方法比較[J].交通運輸工程學報,2008,8(1):36-40.

[14]張向東,閆維明,葛惠娟,等.由國際平整度指數模擬路面不平度方法研究[J].公路交通科技,2009,26(4):13-16.

[15]SunL,ZhangZ,RuthJ.ModelingIndirectStatisticsofSurfaceRoughness[J].JournalofTransportationEngineering, 2001 ,127 (2) : 105-111.

[16]余志生.汽車理論[M].5版.北京：機械工業出版社,2009.

[17]張洪亮.路橋過渡段車路動力學分析及容許差異沉降研究[D].西安:長安大學，2003.