一類三寡頭博弈模型的動力學分析
于晉臣,張彩艷
(1.山東交通學院 理學院,山東 濟南 250357;2.山東電子職業技術學院,山東 濟南 250014)
市場經濟從本質上而言屬于動力系統的范疇,數學表現形式為微分方程或差分方程。在經濟動力學理論中,存在許多微分或差分動力模型,諸如Cournot模型、Stacklberg模型以及Chamblin模型等。基于這些模型,通過對市場經濟系統的穩定性、周期以及混沌行為進行深入研究,得出了一系列結果[1]。
三寡頭博弈是一種基本的寡頭博弈行為,對于典型的基于產量競爭的三寡頭博弈而言,各寡頭廠商同時做出產量決策,其Cournot解是唯一的Nash平衡點。在重復的三寡頭博弈中,各寡頭廠商均把獲取最大收益作為自己追求的目標。三寡頭博弈與真實的市場博弈最接近,鑒于此,已有一些學者對三寡頭博弈的情形進行研究[2-6]。其中,在各寡頭廠商均具有樸素預期的假定下,文獻[2]研究了一類具有相同預期的三寡頭博弈模型,研究表明,該模型的動力學行為非常復雜,出現了周期甚至混沌行為。文獻[3]將文獻[7]的Kopel雙寡頭博弈模型推廣到三寡頭情形,并研究了該模型的多穩定性。文獻[6]研究了電力市場上三寡頭博弈模型的復雜性。
本文研究的三寡頭博弈模型基于這樣的假定:2個寡頭廠商為有限理性預期,另1個寡頭廠商為自適應預期,并且均生產同質產品。這樣,由于市場容量有限,為防止競爭而引起價格戰現象,寡頭廠商會理智的選擇聯合起來形成定價同盟,避免不必要的利潤損失。因而,在價格相同的前提下,產量高的廠商可以通過產量優勢銷售更多的產品(買方需求很大,幾乎處于產多少要多少的狀態),從而獲取最大利潤。顯然,若以產量和產量調整速度作為變量可以在某種程度上反映廠商的生產規模以及產品的市場占有率。
考慮到現實市場中產量與成本費用并非具有簡單的線性關系,本文在非線性成本函數的基礎上建立產量博弈模型。各寡頭廠商實際上對市場的調節、反應能力不同,故不同廠商的產量關系結構也會有所區別。此外,寡頭廠商通常會有信息不對稱的問題,即使信息對稱,對信息的處理能力也各不相同。因此,本文將非線性成本函數、線性逆需求函數和不同產量決策等因素引入到Cournot模型中,建立了三寡頭產量博弈模型,使得更加貼近真實寡頭競爭的市場情況,并以此為基礎研究競爭過程中博弈的復雜性。
1 建模
考慮1個Cournot三寡頭博弈模型。qi表示廠商的產量,i=1,2,3。Q=q1+q2+q3為總供給量,則相同的線性逆需求函數為
p=f(Q)=a-bQ,
(1)
式中p為產品的市場出清價格;a,b為正常數。
廠商i二次可微的成本函數為
(2)
式中ci為正常數,與各企業技術水平成反比。
因此各企業的利潤函數為
(3)
由于假定Cournot三寡頭市場上的產品為同質商品(可完全替代),將式(1),(2)代入式(3)中得到
這個最優化問題有唯一解
現在假定寡頭廠商1和2均為有限理性,也就是說,由于寡頭廠商對市場需求并不完全了解,其產量決策是一個動態過程,在每一階段t寡頭廠商都要對下一階段對手的產量做出一個預期來確定使收益最大化的下一階段的相應產量。用qi(t)表示廠商在t階段時的產量,下一階段的產量qi(t+1)與t階段的邊際利潤息息相關。若邊際利潤為正(負),則將在下一階段增加(減少)產量,動態方程為
式中 αi為正參數,表示廠商i的產量調整速度。
結合式(3),可以得到有限理性寡頭廠商的動態方程為
假定廠商3具有適應性預期的能力,即下一階段的產量q3(t+1)是依據上一階段的產量q3(t)以及反應函數r3(q1,q2)得出的,從而有
q3(t+1)=(1-v)q3(t)+v〔a-b(q1+q2)〕/〔2(b+c3)〕,
式中 v為廠商3的調整速度,v∈[0,1]。
這樣,得到的三寡頭博弈模型為
(4)
式(4)表明,廠商1和2進行產量博弈時,都會根據各自上期邊際利潤的情況進行產量調整。廠商在t階段的邊際利潤為正,則可通過在下一階段增加產量來提高利潤,反之就要減少產量,不然的話利潤就會下降。而廠商3由于采用適應性預期,其調整產量的方式與其余2個廠商不同。從而,三寡頭廠商對產量的調整速度不可能完全相同,這樣就會影響寡頭廠商之間博弈的結果。所以,寡頭廠商對產量的調整速度,即α1,α2,v是影響產量博弈的主要因素。下面就針對α1,α2,v的變化對三寡頭動態博弈過程的影響進行研究。
2 Nash平衡點的存在性以及局部穩定性分析
由于Nash平衡點對真實的市場博弈具有指導意義,因而,盡管式(4)的平衡點很多,本文僅考慮Nash平衡點的存在性以及穩定性。
通過求解下面的非線性方程
為了討論方便,取a=10,b=1,c1=0.15,c2=0.2,c3=0.3,v=0.8,則此時的Nash平衡點為E*(2.474 6,2.297 8,2.010 6)。式(4)在E*的Jacobian矩陣為
故特征多項式為
f(λ)=λ3+Aλ2+Bλ+C,
式中 A=5.691 6α1+5.514 8α2-2.2,B=1.4-7.591 3α1-7.324 8α2+25.701 6α1α2,C=1.899 7α1+1.81α2-9.864 2α1α2-0.2。
從而,確定Nash平衡點的穩定性的計算式[8]為
(5)
因此,若固定v不變,則當α1,a2的取值落在式(5)確定的區域時,Nash平衡點的穩定性不會變化。當α1或α2的取值一旦超出穩定域,系統將變得不穩定,并最終進入混沌狀態。這反映出,在實際的市場博弈中,寡頭廠商尚未達到Nash平衡前,為了獲得更多的利潤,會不斷地進行產量博弈,即不斷調整各自的產量。經過不斷的調整,當處于Nash平衡時,若寡頭廠商對產量的調整速度不快,能落在穩定域時,產量平穩,市場穩定。若任何一方產量調整速度過快,超出了穩定區域,市場會處于波動之中。尤其是系統進入混沌初態時,市場會發生紊亂,陷入動蕩之中,這時需要國家進行宏觀調控來維護市場的穩定。
顯然,若固定α1或α2不變,而對(α2,v)或(α1,v)進行調整時,也有類似的結論。
3 產量調整速度對穩定性的影響
通過上述分析可知,只要寡頭廠商中的任何一方加快調整速度,使得參數取值超出穩定區域,Nash平衡點的穩定性就會發生變化,進而影響各廠商的總體利潤。
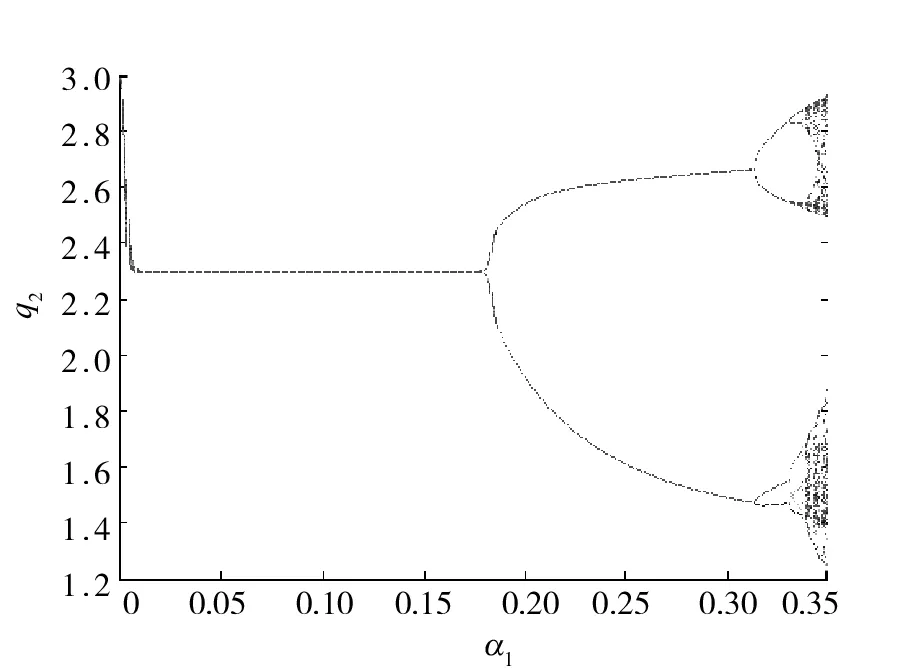
圖1 α2=0.25,v=0.8時,q2關于參數α1的分岔圖
為了更直觀的認識系統的動力學行為,下面采用數值仿真的方法對系統進行分析。首先對各參數賦初值:q1(1)=0.1,q2(1)=0.2,q3(1)=0.3,a=10,b=1,c1=0.15,c2=0.2,c3=0.3。
鑒于3個寡頭廠商的動力學行為完全類似,下面僅以寡頭廠商2為例來說明整個動態博弈過程。
固定寡頭廠商2的調整速度為α2=0.25,廠商3的調整速度為v=0.8。圖1顯示了隨著寡頭廠商1的產量調整速度α1的增大,廠商2的產量演化過程。
寡頭廠商2的產量q2隨著α1的增大,首先達到Nash平衡狀態(q2=2.297 8),而后經歷倍周期分岔過程最終進入混沌狀態,呈現出了復雜而豐富的演化結果。觀察發現,當α1<0.178時,Nash平衡點穩定,即三寡頭廠商的產量處于均衡狀態。隨著α1的增大,平衡點的穩定性發生變化,寡頭廠商的產量出現了倍周期分岔現象。其中α1∈(0.178,0.313),為產量波動的2周期窗口,α1∈(0.313,0.331)為4周期窗口,α1∈(0.331,0.337)為產量波動的8周期窗口,……,最終系統處于混沌狀態。
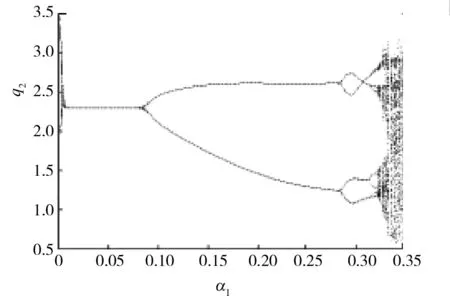
圖2 α2=0.3,v=0.8時,q2關于參數α1的分岔圖
固定寡頭廠商2的調整速度為α2=0.3,廠商3的調整速度為v=0.8。圖2顯示了寡頭廠商2隨著產量調整速度α1變化的分岔情形。
由圖2可知,從α1=0.07開始,隨著α1的增大,產量曲線歷經倍周期分岔過程最終走向混沌。結合圖1,2可以發現,α2取值不同,圖中分岔點的位置和分岔的形態都發生了變化。顯然,當α2變大后,隨著α1繼續增大,寡頭廠商會加快進入混沌狀態,即市場會加速處于紊亂狀況。

圖3 α2=0.25,v=0.95時,q2關于參數α1的分岔圖
這個博弈過程中,分岔點左移,說明在影響分岔點漂移方面,α1與α2有反向相依關系。同時可以發現,增大α2后,寡頭廠商產量分岔的2周期窗口變長,導致系統動力學性質發生變化。
固定寡頭廠商2的調整速度為α2=0.25,廠商3的調整速度為v=0.95。圖3顯示了寡頭廠商2隨著產量調整速度α1變化的分岔情形。
由圖3可知,增大v時,寡頭廠商仍會加快進入混沌狀態。而且,也出現了分岔點漂移現象(向左),因而,在影響分岔點漂移方面,α1與v也存在反向相依關系。
這就說明,無論增大α2還是v,隨著α1的增大,寡頭廠商產量失穩的現象都會提前出現,即市場會提前進入波動狀況。
4 系統的混沌行為分析
為了分析系統的混沌演化過程,下面分別從最大Lyapunov指數和奇異吸引子兩個方面予以說明。
4.1 最大Lyapunov指數
Lyapunov指數表示平均每次迭代引起的指數分離中的指數,描述了相空間內系統中相鄰軌道收斂或發散的平均水平。通過計算Lyapunov指數,可以從定量角度研究混沌系統。一個系統中往往存在多個Lyapunov指數,并不需要一一進行計算,其中具有指標意義的是最大Lyapunov指數。若最大Lyapunov指數為正,則說明系統處于混沌狀態;若最大Lyapunov指數為負,則說明系統穩定。
圖4為固定α2=0.25,v=0.8時,最大Lyapunov指數隨著α1增大時的變化情形。顯然,此時最大Lyapunov指數可以看作α1的函數。
從圖4中很容易觀察到0<α1<0.4時,系統的局部穩定性情形。當最大Lyapunov指數<0時,說明系統穩定;當最大Lyapunov指數=0時,說明出現了分岔現象;當最大Lyapunov指數>0時,說明系統進入混沌狀態。
4.2 奇怪吸引子
當系統處于混沌狀態時,會出現奇怪吸引子。如前文所述,隨著α1的增大,Nash平衡點失穩,會導致系統離開穩定區域,并通過倍周期分岔,最終進入混沌狀態。取a=10,b=1,c1=0.15,c2=0.2,c3=0.3,α1=0.36,α2=0.25,v=0.8,可以得到系統的相圖如圖5所示。
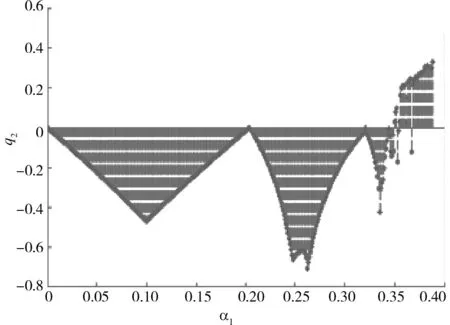
圖4 q2關于參數α1的分岔圖
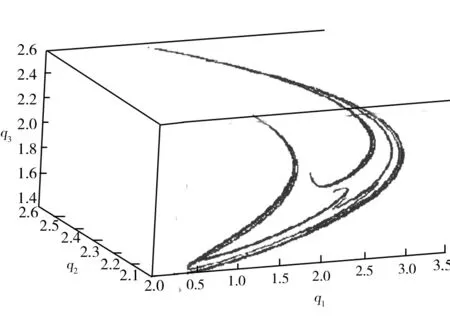
圖5 系統的相圖
5 結論
本文建立了三寡頭博弈模型,分析了Nash平衡點的穩定性,并對博弈的過程進行了數值模擬。結果表明,市場穩定程度與產量調整速度呈反向變動關系;從規避風險的角度考慮,均衡狀態是博弈各方都比較滿意的狀態。這就為真實市場中寡頭廠商的競爭策略選擇和政府宏觀調控方式提供了借鑒。
參考文獻:
[1]Yang H, Zhang Y. Complex Dynamics Analysis for Cournot Game with Bounded Rationality in Power Market[J].Journal of Electromagnetic Analysis and Applications,2009,1(1):48-60.
[2]Puu T. Chaos in Duopoly Pricing[J].Chaos,Solitons & Fractals,1991,1(6):573-581.
[3]Agiza H N, Bischi G I, Kopel M. Multistability in a Dynamic Cournot Game with Three Oligopolists[J].Mathematics and Computers in Simulation,1999,51(1-2):63-90.
[4]Agiza H N. Explicit Stability Zones for Cournot Games with 3 and 4 Competitors[J].Chaos, Solitons & Fractals, 1998,9(12):1955-1966.
[5]Elabbasy E M, Agiza H N, Elsadany A A ,et al. The Dynamics of Triopoly Game with Heterogeneous Players[J].International Journal of Nonlinear Science, 2007,3(2):83-90.
[6]Ma J, Ji W. Complexity of Repeated Game Model in Electric Power Triopoly[J].Chaos, Solitons & Fractals, 2009, 40(4):1735-1740.
[7]Kopel M. Simple and Complex Adjustment Dynamics in Cournot Duopoly Models[J].Chaos, Solitons & Fractals,1996,7(12):2031-2048.
[8]陳士華,陸君安.混沌動力學初步[M].武漢:武漢水利電力大學出版社,1998.

