基于蒙特卡洛法的常用玻璃量器容量測量結果不確定度評定

趙琳，李鎖印，許曉青，韓志國，馮亞南

(中國電子科技集團公司第十三研究所，河北 石家莊050051)

0 引言

常用玻璃量器(以下簡稱量器)廣泛應用在石油化工、食品衛生、環境檢測等實驗分析工作中。它包括滴定管、分度吸量管、單標線吸量管、單標線容量瓶、量筒和量杯六類玻璃量器，作為化學分析中最基礎的計量器具，其準確度直接影響后續的分析結果。為了確保其計量數據的準確，量器的檢定是非常重要和必要的。

量器的檢定依據JJG196 －2006 《常用玻璃量器檢定規程》進行，規程中對常用玻璃量器的容量允差進行了詳細的規定，但仍不能滿足一些行業部門對量器不確定度的要求。本文選用單標線容量瓶，對其進行不確定度分析，以滿足各行各業應用玻璃量器的實驗室的需要。容量測量結果不確定度的評定是我們建立“常用玻璃量器檢定裝置”和開展檢定工作重要的依據。

1 測量不確定度分析

測量不確定度是與測量結果相聯系的、表征合理地賦予被測量分散性的參數。從詞意上理解，測量不確定度意味著對測量結果可信性、有效性的懷疑程度或不肯定程度，是定量說明測量結果的質量的一個參數。測量不確定度的評定方法有很多種，通常情況下是依據GUM 法對不確定度進行評定，但是當遇到以下情況時依據GUM 法進行評定得到的結果可能變得不可靠，如:①不宜對測量模型進行線性化等近似的場合;②輸出量的概率密度函數(PDF)較大程度地偏離正態分布或t 分布，例如分布明顯不對稱的場合。蒙特卡洛法(MCM)比較適合這些情況下對不確定度的評定。MCM 法的主要特點為:

1)對于復雜或非線性模型，尤其是無需使用一階或高階偏導來提供不確定度傳播律的靈敏系數，可減小分析難度。

2)非線性模型時，一般可改善輸出量的估計。

3)非線性模型時，尤其是當各個輸入量服從非正態(如不對稱)概率密度函數(PDF)時，無需提供高階導數即可改善輸出量的估計的標準不確定度。

4)當輸出量的PDF 不能由正態分布或縮放位移t分布充分近似時，即無法應用中心極限定理時，可提供給定包含概率下的包含區間。以下情況會出現不適當的近似:①一個占主導地位輸入量的PDF 不是正態分布或縮放位移t 分布;②模型非線性;③使用公式Welch－Satterthwaite 計算有效自由度時，引入的近似誤差不可忽略。

5)確定包含區間時無需包含因子。

量器檢定規程中給出的玻璃量器容量的數學模型比較復雜，基于以上MCM 方法的特點，在評定其測量不確定度時可以選用MCM 法，本文采用MATLAB 軟件編程實現。

2 采用MCM 方法對量器標準不確定度的分析與評定

按照JJG196 －2006 《常用玻璃量器檢定規程》的要求，檢定方法采用衡量法，通過測量容器內所容納的工作介質的質量和密度，根據檢定規程提供的公式算出被測玻璃量器在標準溫度20℃時的實際容量。本文選用100 mL 單標線容量瓶，采用MCM 法對其不確定度進行分析，評定出不確定度結果，其他的可以參照此不確定度分析過程。

2.1 測量模型

檢定規程中給出了玻璃量器容量的數學模型，如下所示:

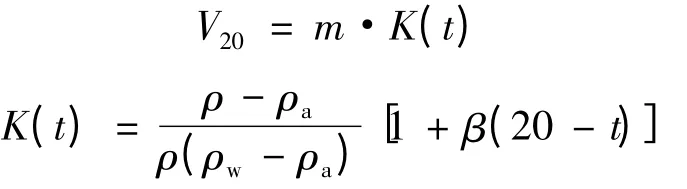
式中:V20為標準溫度20℃時的被檢玻璃量器的實際容量，mL;ρ 為砝碼密度，取8.00 g/cm3;ρa為測定時實驗室內的空氣密度，取0.0012 g/cm3;ρw為蒸餾水t℃時的密度，g/cm3;β 為被測玻璃量器的體脹系數，℃－1;t 為檢定時蒸餾水的溫度，℃;m 為被檢玻璃量器內所能容納水的表觀質量，g。

模型的輸出量為V20，輸入量為m，ρa，ρ，ρw，β和t。

2.2 設定概率密度函數PDF

當輸入量相互獨立時，可根據一系列測量值的分析，或根據某些歷史數據、校準數據和專家判斷之類的信息所得到的科學判斷，為各輸入量設定PDF。本例中各輸入量服從的分布、最佳估計值以及標準不確定度均列入表1 中。

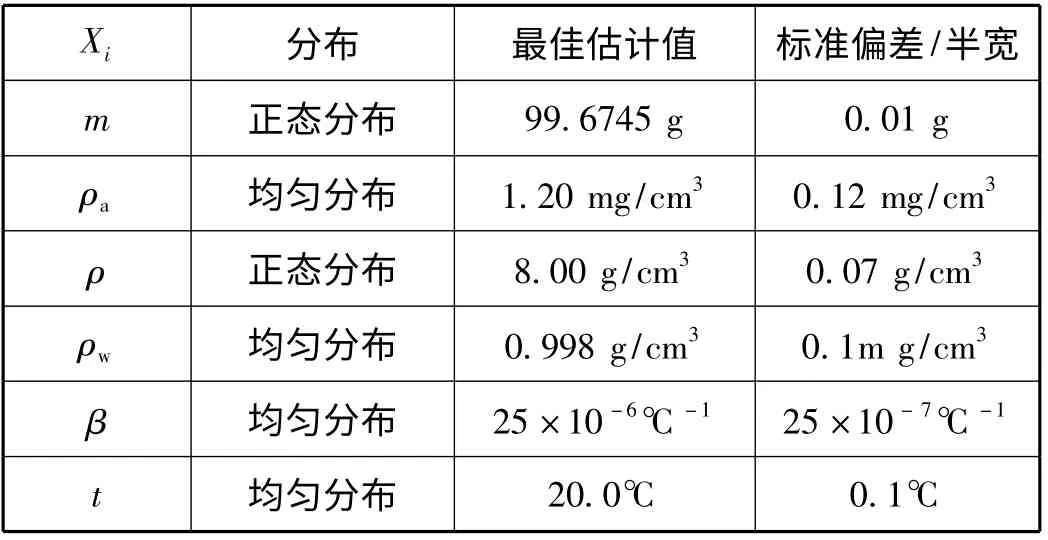
表1 關于量器測量模型的輸入量及其概率密度函數

表1 中，水表觀質量(m)的相關信息是通過使用衡量法重復測量10 次得到，測量值分別為:99.6752， 99.6893， 99.6682， 99.6723， 99.6710，99.6891，99.6688，99.6705，99.6710，99.6690 g，測量結果平均值和其標準不確定度按下面公式分別計算為

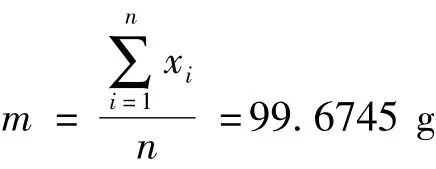
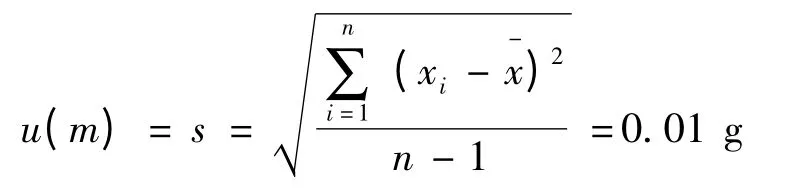
空氣密度ρa、體積膨脹系數和溫度的相關信息是由JJG196 －2006 《常用玻璃量器檢定規程》檢定規程得到;砝碼的密度信息是通過JJG99 －2006 《砝碼》檢定規程中給出的典型材料密度表中查表得到;蒸餾水的密度信息是通過查閱資料得到。

2.3 結果報告

在規定的數值容差下MCM 所提供的結果所需的試驗次數跟輸出量的PDF “形狀”及包含概率有關，應合理選擇蒙特卡洛試驗次數即樣本量的大小M，一般情況下取M=106，這樣通常會為輸出量提供95%包含區間，該包含區間長度被修約為1 或2 位有效十進制數字。應用MCM 法對量器的不確定度進行評定，采用MATLAB 軟件進行編程，部分程序如下所示:

clc;clear; %清除MATLAB 中的變量。

M=1000000; %設定蒙特卡洛試驗次數。

m=normrnd (99.6745，0.01，1，M); %水表觀質量采樣值(g)。

ρA= (0.24* rand (1，M) +1.08)* 10^ －3; %空氣密度(g/cm3)。

ρB=normrnd (8，0.07，1，M); %砝碼密度(g/cm3)。

ρw=0.0002* rand (1，M) +0.9979; %蒸餾水密度(g/cm3)。

β= (5* rand (1，M) +22.5)* 10^ －6; %體積膨脹系數(℃－1)。

t=0.2* rand (1，M) +19.9; %溫度(℃)。

V=m. * (rb － ra). * (1 + b. * (20 － t)). / (rb. *(rw－ra));%衡量法數學模型。

s=std (dm); %輸出量標準不確定度。

avg=mean (dm); %輸出量估計值。

y=sort (dm); %將試驗結果從小到大進行排列。

y_ low=prctile (y，2.5); %包含概率為95%時，包含區間的下限值。

y_ high=prctile (y，97.5); %包含概率為95%時，包含區間的上限值。

運行此程序得出100 mL 單標線容量瓶平均值為99.979 mL，標準不確定定度為:0.013 mL;包含概率為95%;包含區間為［99.955 mL，100.006 mL］。

運行程序得到輸出量概率密度分布的結果圖如圖1所示。

3 采用GUM 方法對量器標準不確定度的分析與評定

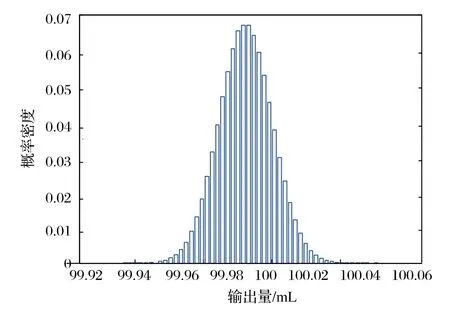
圖1 輸出量近似概率密度分布圖

采用GUM 方法評定量器的不確定度時，數學模型與采用MCM 法評定時的測量模型一致，在此評定過程中，令Dρ=，Dt= 1 + β(20 － t)，則數學模型可以簡化為

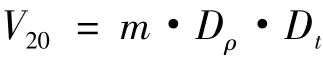
分析此數學模型，得知其不確定度分量包括:①檢定點測量重復性引入的不確定度;②質量測量引入的不確定度;③密度引入的不確定度，包括砝碼密度、空氣密度、水的密度;④溫度引入的不確定度，包括體脹系數、溫度測量引入的不確定度。

同樣的選取100 mL 單標線容量瓶對其不確定度進行分析，靈敏系數由簡化后的數學模型直接求得，最后利用表1 中輸入量的相關信息評定出其容量平均值為99.978 mL，合成標準不確定度uc= 0.015 mL，包含概率為95%，包含區間為［99.948 mL，100.008 mL］。這一結果比采用MCM 法的評定結果要大，但是均滿足玻璃量器規程中的要求。

4 總結

通過采用MCM 法對玻璃量器的不確定度進行了評定，并將此方法的評定結果與GUM 方法的評定結果進行了比較，兩者之間雖然存在細微的差異，但是這些結果都滿足玻璃量器檢定規程的要求。按照JJF1059.2－2012 中使用MCM 驗證GUM 的要求，GUM 法通過了驗證，在以后進行量器容量的測量不確定度評定時，可以使用GUM 法進行評定。本文主要是以單標線容量瓶為例進行了評定，其他類型的玻璃量器也可依據此方法進行評定，但是在評定的過程中要注意以下幾個問題:

1)一般情況下，GUM 方法的評定結果比MCM 方法評定的結果略顯保守，這主要是由于在評定過程中，某些不確定度分量被重復計入和計量人員對不確定度分量的理解程度不同造成的。

2)對于滴定管、分度吸量管、量筒、量杯等多刻度線的量器的不確定度評定，應根據用戶的需求進行單一刻度線的具體分析，給出該刻度線的不確定度評定結論。

［1］國家質量監督檢驗檢疫總局.JJG 196 －2006 常用玻璃量器檢定規程［S］. 2006.

［2］周桃庚. 用蒙特卡洛法評定測量不確定度［M］. 北京:中國計量出版社，2012.

［3］國家質量監督檢驗檢疫總局.JJF1059 －2012 測量不確定度評定和表示［S］. 2012.

［4］國家質量監督檢驗檢疫總局. JJG99 －2006 砝碼檢定規程［S］. 北京:中國計量出版社，2006.