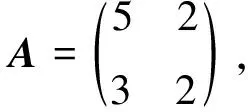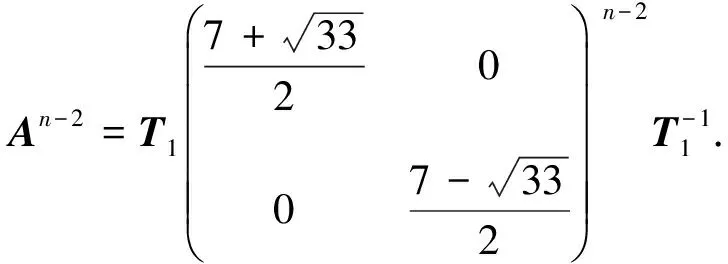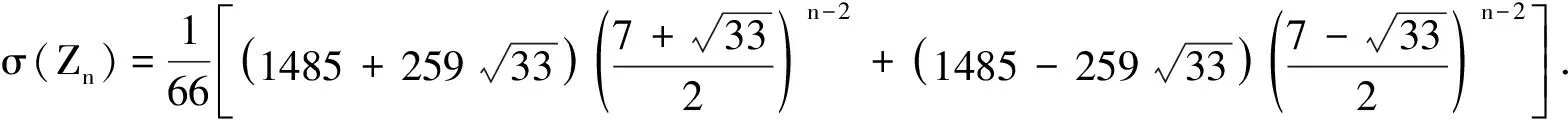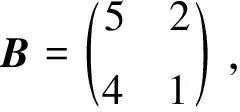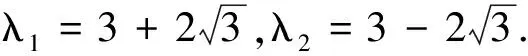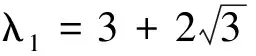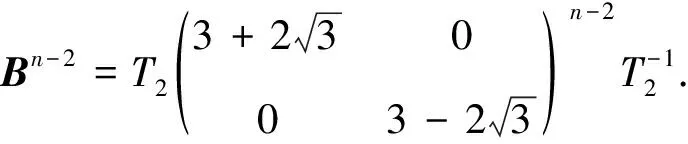四角鏈的Merrifield-Simmons指標
田文文, 田雙亮
(西北民族大學 數學與計算機科學學院, 甘肅 蘭州 730030)
1 預備知識
設G=(V,E)是一個簡單圖,它的點集和邊集分別為V(G)和E(G).令e和x分別為圖G的一條邊和一個頂點,我們用G-e表示圖G刪去邊e得到的圖,用G-x表示圖G刪去頂點x(及關聯的邊)得到的圖.若A?V(G),對任意的兩個頂點u,v∈A,都有uv?E(G),則稱A為圖G的一個獨立集,其中空集為任何圖的一個獨立集.本文中Fn表示Fibonacci數,即滿足Fn=Fn-1+Fn-2,n≥2,且F0=0,F1=1.文中未加說明的符號及術語參見文獻[1].
Merrifield-Simmons指標是1989年由美國化學家Richard E.Merrifield和Howard E.Simmons在文獻[2]中引入的化學拓撲指標.它表示圖G中所有獨立集的數目,記為σ(G).該指標與物質的沸點有著密切的聯系,且有著較為廣泛的應用,有關的應用及部分最新研究成果參見文獻[2-4].文獻[5]中對兩類四角系統的匹配數與點獨立集數進行了研究.文獻[6]中研究了關于k-匹配和k-獨立集的極值四角鏈.本文通過構造一類特殊的四角鏈,即由n個單位正方形序列且任意相鄰兩個正方形之間只有一條割邊構成的連通圖,研究該類四角鏈在兩種不同構聯接位下的Merrifield-Simmons指標,并給出具體表達式.
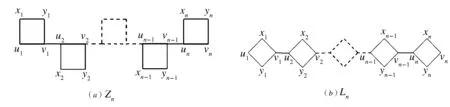
定義1設Q1,Q2,…,Qn為n個單位正方形序列,則稱該序列為四角鏈,如果滿足:
(i)對任意的1≤s (ii)每個正方形與割邊的頂點都為3度頂點. 用Φn表示含有n個單位正方形構成的四角鏈的全體.設Gn∈Φn,一個四角鏈Gn(n≥2)可由Gn-1再聯接一個單位正方形得到,如圖1所示.每個鏈中的正方形有3個可聯接位,但其中與接點距離相等的2個可聯接位1和1′是同構的,所以只有兩種非同構的聯接方式Gn-1→[Gn-1]k=Gn,其中k=1,2分別稱為1-位聯接和2-位聯接. 圖1 兩種連接方式 特別地,若四角鏈Gn中的每個單位正方形都以1-位聯接的方式聯接在前一個正方形上,則記為Zn;若四角鏈Gn中的每個單位正方形都以2-位聯接的方式聯接在前一個正方形上,則記為Ln,如圖2所示. 圖2 四角鏈Zn和Ln 在證明主要結論之前,我們先介紹以下幾個引理: 引理1[4]設G是一個圖,對?uv∈E(G),u∈V(G) ,令NG[u]={u}Y{v|uv∈E(G)}, 則有σ(G)=σ(G-u)+σ(G-NG[u]). 引理3[4]設Pn為n階的路,則σ(Pn)=Fn+2. 引理4[4]設Cn為n階的圈,則σ(Cn)=Fn+1+Fn-1. 關于四角鏈在兩種非同構聯接位下的Merrifield-Simmons指標,我們可以得出以下的結論. 定理1對于任意的正整數n≥2,有 證明如圖2所示,根據引理可得 (i)因為σ(Zn)=σ(Zn-un)+σ(Zn-NZn[un])=σ(P3)·σ(Zn-1)+σ(P1)·σ(Zn-1-vn-1)= F5·σ(Zn-1)+F3·σ(Zn-1-vn-1)=5σ(Zn-1)+2σ(Zn-1-vn-1)= σ(Zn-vn)=σ(Zn-vn-un)+σ(Zn-vn-NZn-vn[un])=σ(P2)·σ(Zn-1)+σ(P1)·σ(Zn-1-vn-1)=F4·σ(Zn-1)+F3·σ(Zn-1-vn-1)=3σ(Zn-1)+2σ(Zn-1-vn-1)= (ii)因為σ(Ln)=σ(Ln-un)+σ(Ln-NLn[un])=σ(P3)·σ(Ln-1)+σ(P1)·σ(Ln-1-vn-1)= F5·σ(Ln-1)+F3·σ(Ln-1-vn-1)=5σ(Ln-1)+2σ(Ln-1-vn-1)= σ(Ln-vn)=σ(Ln-vn-un)+σ(Ln-vn-NLn-vn[un])=σ(P1)·σ(P1)·σ(Ln-1)+σ(Ln-1-vn-1)= F3·F3·σ(Ln-1)+σ(Ln-1-vn-1)=4σ(Ln-1)+σ(Ln-1-vn-1)= 定理2對于任意的正整數n≥2,有 [1] Bondy J A,Murty U S R.Graph Theory with Applications[M].New York:The Macmillan Press,1976. [2] Hosoya H.Topological index[J].Bull Chem Soc Japan,1971,44:2 332-2 339. [3] Merrfield R E,Simmons H E.Topological Methods in Chemistry[M].New York:Wiley,1989. [4] Gutman I,Polansky O E.Mathematical Concepts in Organic Chemistry[M].Berlin:Springer,1986. [5] 張蓮珠.兩類四角系統的匹配數與點獨立集數[J].數學研究.1999,32(3):310-315. [6] Zeng Y Q,Zhang F J.Extremal polyomino chains onk-matchings andk-independent sets[J].Journal of Mathematical Chemistry,2007,42(2):125-140.
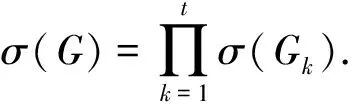
2 主要結論及其證明
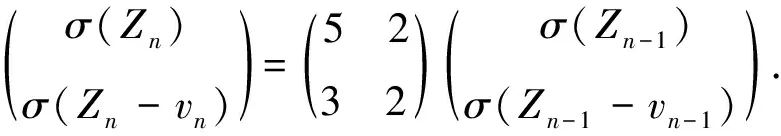



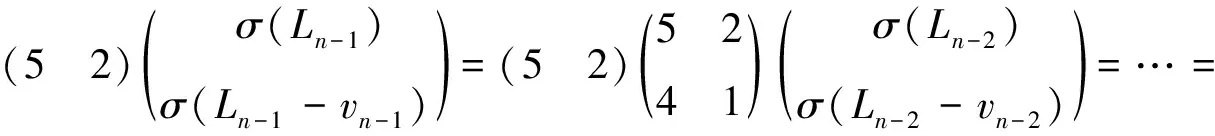

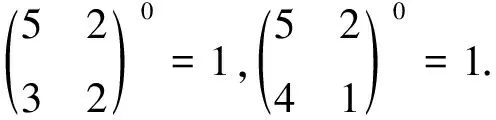
3 進一步的結果