Weibull分布型元件串聯系統的可靠性廣義置信區間
盧勤勤, 李新民, 張 霞
(1.山東理工大學 理學院, 山東 淄博 255091; 2. 青島大學 數學科學學院, 山東 青島 266071; 3. 山東省淄博市公路管理局, 山東 淄博 255000)
Weibull分布廣泛應用于可靠性工程,是可靠性工程中重要的分布,其概率密度為
(1)
其中λ>0為尺度參數,k>0為形狀參數.其在t時刻的可靠度函數
對于單個Weibull分布型元件的定時結尾數據的可靠性函數的置信區間已得到較好解決[1],但對于有兩個Weibull分布型元件組成的串聯系統,卻極少有文獻對其系統可靠性的置信區間進行研究.本文將基于Weerahandi[2]的廣義樞軸量和廣義置信區間的概念,建立系統可靠性的廣義置信區間.因此,本文中對廣義樞軸量和廣義置信區間的基本概念和理論進行介紹,然后基于服從Weibull分布的兩個元件的定時結尾數據構造了R(t)廣義樞軸量以及其廣義置信區間,并且在此基礎上,又討論了廣義置信區間的頻率性質.并從理論上證明了由廣義樞軸量所確定的可靠性的廣義置信區間就是頻率意義下的實際置信水平.
1 可靠性函數的廣義置信區間
1.1 串聯系統的可靠性
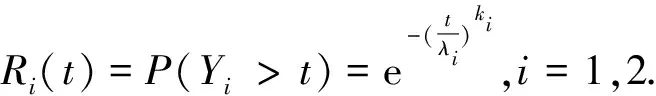
R(t)=R1(t)R2(t)=
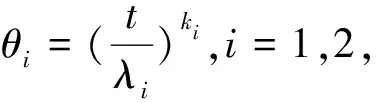
1.2 廣義置信區間
由于討厭參數的存在,很難利用傳統的建立置信區間的方法得到精確的置信區間. Weerahandi[2]給出了廣義區間估計的概念.設X為觀測向量,其密度函數為f(x,ξ),ξ=(θ,η)為未知參數,其中θ∈Θ為興趣參數,η為討厭參數.令T=t(X;x,ξ)是X,x和ξ的函數,如果T滿足以下兩條性質:
(i)?x,T的概率分布Px與未知參數無關;
(ii)若X=x,t(x;x,ξ)不依賴于討厭參數η,則稱T為廣義樞軸量.
于是,對給定的置信水平γ,任意給定x,可以定義θ的廣義置信區間.
1.3 基本構造方法
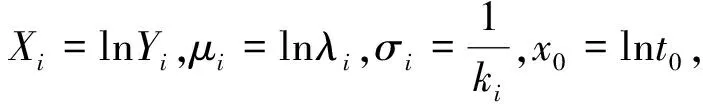
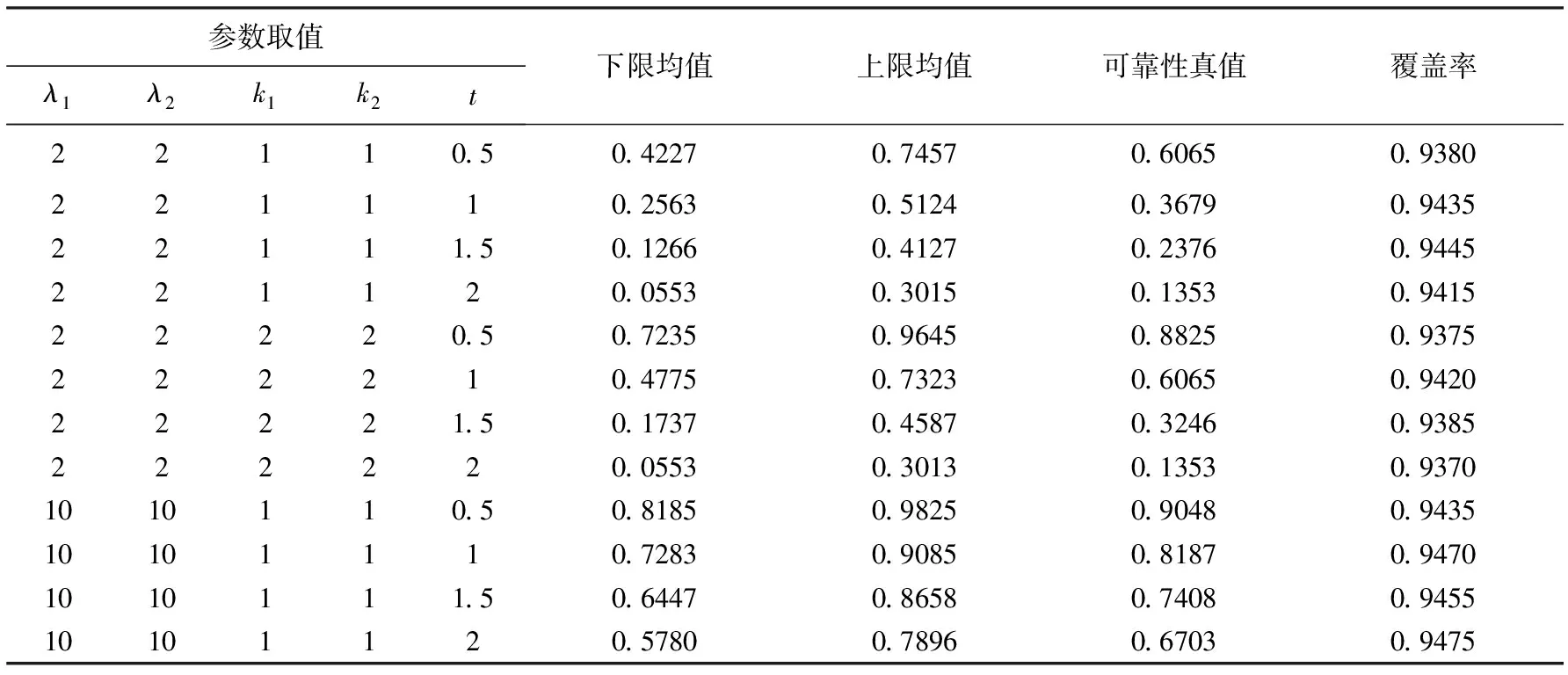
其中,函數f(t)=ete-et,-∞ (2) (3) 則,由Hannig等[6]知,μi和σi的Fiducial模型為 (4) 于是θ1+θ2的Fiducial模型為 (5) (6) 由于求解可靠性R(t)的廣義樞軸量的精確分布比較困難,下面給出了計算廣義置信區間的模擬計算方法,步驟如下: 1)對于給定樣本數據Y1,Y2,…,Yn1和Y1,Y2,…,Yn2我們通過換元的方法,令Z=lnY得到服從極值分布的定時截尾壽命數據Z1,Z2,…,Zn1,Zn1+1,Zn1+2,…,Zn1+n2. 4)由以上數據及公式(5),計算Tθ1+θ2的觀測值為T(θ1+θ2)i. 5)將T(θ1+θ2)i由大到小排序,的到其順序統計量T(θ1+θ2)(1) (exp(-T(θ1+θ2)(U)),exp(-T(θ1+θ2)(L))). 廣義置信區間的覆蓋率并不一定等于我們要求的置信水平,下面將通過數值模擬的方法研究所得可靠性函數R(t)的廣義置信區間的頻率性質. 對于由兩個獨立的Weibull元件組成的串聯系統,兩Weibull分布的樣本容量分別為n1=n2=10,并且當形狀參數取值為k1=k2=1時,尺度參數分別為λ1=λ2=2,10;當k1=k2=2時,尺度參數分別為λ1=λ2=2,置信水平為1-α=0.95,模擬次數為M=1 000次.在計算R(t)的廣義置信區間時,對于每一個樣本數據,標準極值分布的樣本容量均為N=1 000次.計算結果見表1. 表1 可靠性函數的廣義置信區間的覆蓋率 從表1中可以看出,可靠性函數的廣義置信區間覆蓋率比較穩定,且當尺度參數較大時比較接近真實的置信水平. 本文對由兩個獨立的兩參數Weibull分布分別組成的串聯系統,利用廣義樞軸量以及廣義置信區間的概念,將原樣本數據換元后得到服從極值分布的樣本數據,構造其所需要的Fiducial模型,建立了它的可靠性函數的廣義置信區間,并給出了計算R(t)的廣義置信區間的算法.模擬結果表明廣義置信區間的覆蓋率比較令人滿意. [1]趙桂梅,崔玉杰.Weibull分布興趣參數的廣義置信區間[J].工程數學學報, 2010,27(6):567-570. [2] Weerahandi S. Generalized confidence intervals[J]. JAmer Statist Assoc, 1993,88: 899-905. [3] 董巖,徐興忠.雙參數指數分布型元件串聯系統的可靠性的廣義置信區間[J].應用數學學報, 2011,34(6):1 023-1 031 [4] 徐興忠,李國英.樞軸分布族中的Fiducial推斷[J].中國科學:A輯,2006,36(3):340-360. [5] Hannig J, Iyer H, Patterson P.Fiducial generalized confidence interval[J]. J Amer Statist Assoc, 2006,101: 254-269.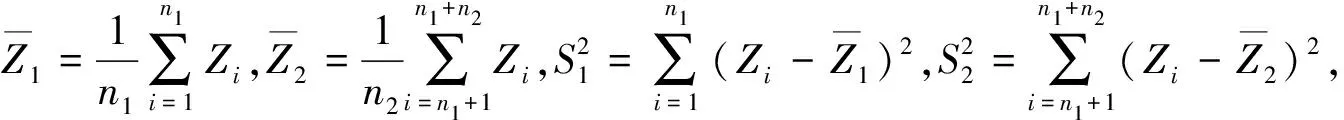
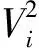
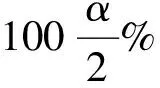
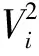
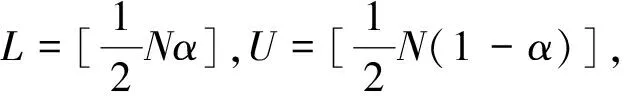
2 模擬計算
3結束語

