抗反輻射導彈兩點源誘偏技術研究

韓紅斌，顧振杰，徐東東，劉 宇

（中國人民解放軍91336部隊，河北 秦皇島066326）

0 引言

反輻射導彈（ARM）是一種利用敵方雷達輻射源的電磁波進行導引并攻擊該雷達及其載體的導彈［1］。在現代戰爭中，ARM 對雷達的威脅越來越大，對雷達的作戰效能和生存能力提出了嚴峻的挑戰。目前，應對ARM 的措施主要有：建立專門的ARM 告警系統、采用先進的雷達體制、采用雷達誘餌技術和硬殺傷技術，其中，雷達誘餌技術是一種經濟有效的對抗措施。

雷達誘餌技術是通過多個輻射源的布陣在空間產生一個合理的合成場分布，對ARM 進行誘偏，從而實現對雷達和誘餌的雙重保護［2］。本文利用合成場原理，運用等相位面的梯度推導出了多點源誘偏誤差公式，并對兩點源誘偏進行了研究，仿真分析了兩點源的誘偏效果，獲得了一些對誘餌實際部署有指導性的結論。

1 多點源的合成場和誘偏公式

雷達、誘餌與ARM 的幾何關系如圖1所示。

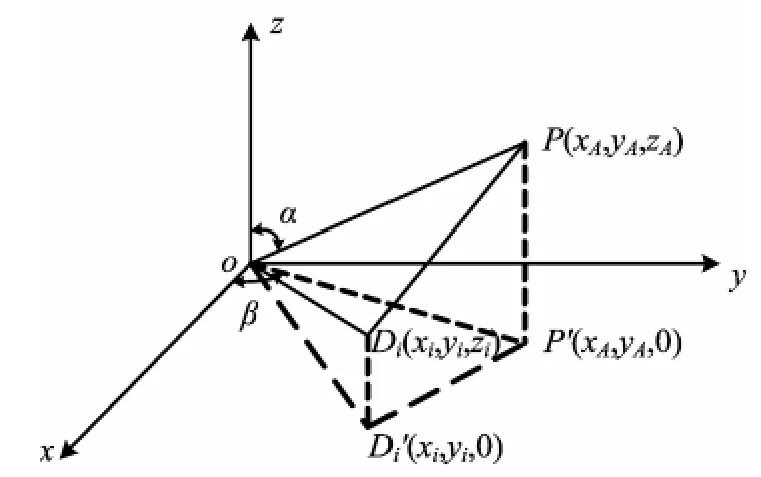
圖1 雷達、誘餌與ARM 的幾何關系

令被保護雷達位置為坐標原點，第i個輻射源坐標是（xi，yi，zi），t 時 刻ARM 的 空 間 坐 標 位 置 為P（xA，yA，zA），t時 刻 各 輻 射 源 與ARM 導 引 頭 的 斜距為：

ARM 處的合成場矢量、合成場的幅度和相位分別為：

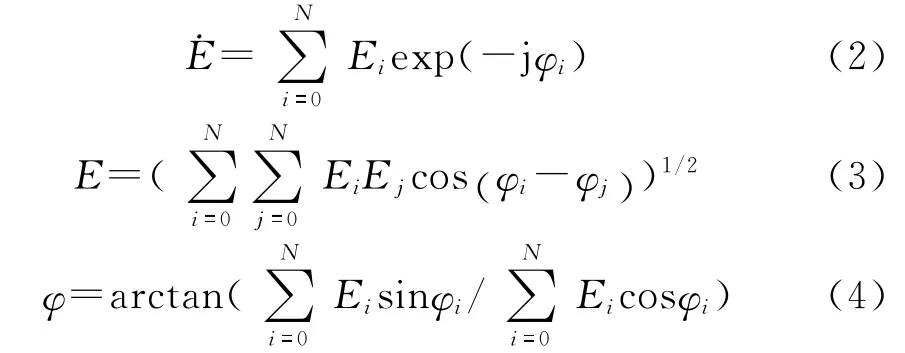
式中：

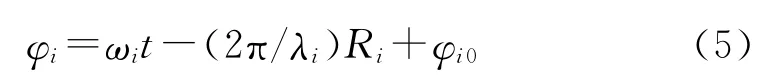
令雷達發射信號為參考信號，誘餌信號相對于雷達發射信號的初始相位差是φi0，φ00為0。

等相位面的梯度為：

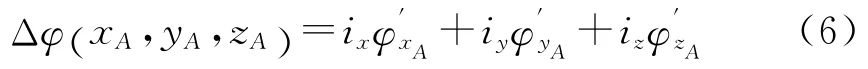
式中，合成波陣面的法線方程為：

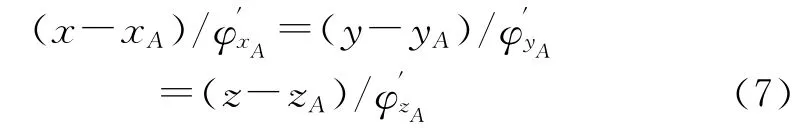
令z為0，由上述法線方程，可得空間任一點的梯度向量同xoy 平面的交點，即位于P（xA，yA，zA）處的ARM 直接攻擊時的可能的彈著點為：

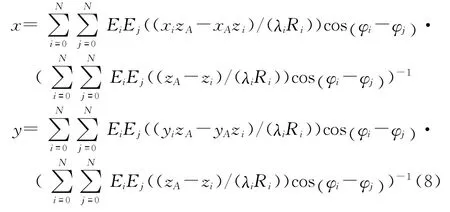
2 兩點源誘偏分析

兩點源誘偏平面坐標系如圖2所示。

圖2 兩點源誘偏平面坐標系

圖2中，A 為ARM，雷達為坐標原點O（0，0），誘餌為x 軸上點O1（d，0），將式（8）化簡，得到法線與地面的交點O′坐標為：

式中：

由式（9）可知，ARM 的瞄準方向跟相位差Δφ、點源的工作波長以及點源到導引頭的電場強度峰值有關。誘餌與雷達的輻射電場峰值相同，即β 為1 時，ARM 導引頭瞄準方向隨Δφ、K 的變化曲線如圖3所示。

圖3 β＝1時導引頭瞄準方向變化曲線

由圖3可以看出，當β為1時，ARM 導引頭瞄準方向與相位差Δφ 無關，隨著K 的增大導彈的瞄準方向偏向雷達，這是由于隨著K 的增大，誘餌的頻率偏離雷達的頻率，偏到導彈可以分辨雷達和誘餌時，導彈跟蹤雷達。因為導彈與雷達和誘餌的距離很遠，它們的距離差忽略不計，而誘餌的中心頻率和雷達的一樣，所以K 在1 的附近變化。在K 為1 的附近觀察ARM 的瞄準方向，如圖4所示。

圖4 K＝1的附近時的導彈瞄準方向

由圖4可以看出，當雷達和誘餌的輻射電場峰值相同時，導彈瞄準兩點源的中間點附近。取β為1.2、K 取不同值時，ARM 導引頭瞄準方向隨相位差Δφ 的變化曲線如圖5所示。

圖5 β＝1.2時導引頭瞄準方向變化曲線

由圖5可以看出，Δφ∈（π／2，3π／2）時，導彈的瞄準方向動蕩劇烈，Δφ∈（0，π／2）和Δφ∈（3π／2，2π）時，導彈的瞄準方向相對穩定。圖5 的局部放大如圖6所示。

圖6 局部放大圖

由圖6可以看出，隨著K 的增大，導彈的瞄準方向偏向于雷達。且在相位差Δφ 小于π／2 時，導彈的瞄準方向比較穩定。

取K 為1、β取不同值時，ARM 導引頭瞄準方向隨相位差Δφ 變化的曲線如圖7所示。

圖7 K＝1時導引頭瞄準方向變化曲線

由圖7可以看出，隨著β值的增大，導彈的瞄準方向偏向于誘餌，這是由于誘餌的輻射功率漸大于雷達的輻射功率，而ARM 導引頭跟蹤功率重心，從而瞄準方向逼近誘餌。實際情況下，輻射源間的功率比不能大于1.25，否則，導引頭將不再跟蹤輻射源的功率重心，而是跟蹤功率大的輻射源［4］。

反輻射武器攻擊目標時分為兩個階段。當離目標較遠時，兩點源還都在導引頭的分辨角θR范圍內，導引頭將跟蹤二者的合成輻射場的法線方向；當ARM抵近目標飛行時，兩點源與導引頭瞄準軸方向之間的夾角變大，當增加到一定程度越過閾值，即θ大于等于θR時（θ為ARM 與兩點源的夾角），ARM 可以分辨出兩個輻射源，此時導引頭穩定跟蹤單一目標雷達或誘餌。在ARM 分辨出目標后，將以最大過載修正初始誤差。此時，若兩點源間距足夠大，則ARM 能夠較早分辨出目標，從而有足夠的時間修正誤差，最終有可能擊中目標；若兩點源間距很小，則ARM 只能在離目標較近的距離上分辨出兩點源，由于ARM 的速度很快，其過載能力有限，很難在短距離內修正誤差，但因為兩點源的間距小，ARM 在擊中兩點源之間某處時，有可能其中一個點源在導彈的殺傷半徑內，也會達到毀傷目標的目的，所以，選擇合適的兩點源間距很重要。

ARM 在達到臨界點時，即θ大于等于θR時，會穩定跟蹤兩點源中的其中一個，在導引期間可修正誤差距離為：

式中，jmax為nmaxg，nmax為ARM 最大過載，g為重力加速度；vrel為ARM 徑 向 速 度；R 為ARM 到O′點 的距離。

當雷達和誘餌的載頻、功率相同時，ARM 的瞄準方向與兩點源間的夾角相等，即瞄準方向是點源與ARM 夾角的角平分線。如圖2所示，圖中α 為ARM進攻角，O″為導彈以最大過載修正誤差后的最終落點，θR為ARM 分辨角。經計算得：

對式（9）化簡得：

導彈最終落點為：

對某型ARM 進行仿真，假設導彈向雷達所在的方向偏，取重力加速度g 為9.8m／s2，最大轉彎過載nmax為8，導彈的徑向速度vrel為1200m／s，導彈分辨角θR為12°，K 為1。對導彈最終落點在進攻角α取不同值時隨兩點源間距的變化進行仿真，結果如圖8所示。

圖8 θR＝12°不同攻擊角時的彈著點

從圖8中可以看出，在確定了反輻射武器的進攻方位后，彈著點到雷達的距離與導彈導引頭跟蹤處于隨遇平衡狀態時的攻擊角α有關，攻擊角α越大，彈著點距離雷達越近，攻擊角α 越小，彈著點距離雷達越遠。再取進攻角α 為55°，對導彈最終落點在分辨角θR取不同值時隨兩點源間距的變化 進行仿真，結果如圖9所示。

圖9 α＝55°不同分辨角時的彈著點

從圖9 中可以看出，θR越小，彈著點距離雷達越近，這是由于當分辨角比較小時，導彈能夠在較遠的距離上分辨出目標，從而及時修正誤差。由仿真結果可知，分辨角對ARM 的抗誘偏性能影響很大。目前導引頭的分辨角由常規的6～12°優化到5～6°，對于誘餌的誘偏能力要求更為苛刻。

3 結束語

本文從場的角度推導出了多點源誘偏的通用公式，并對兩點源誘偏進行了仿真分析。通過仿真實驗結果可知，在進行雙點源誘偏時，應使誘餌和雷達的功率和中心頻率相同，且應根據ARM 具體的攻擊角和分辨角來合理布置誘餌和雷達之間的距離，使誘偏效果最佳。本文在推導時未考慮雷達方向圖對誘偏效果的影響，實際誘偏時也不止一個誘餌，這些問題有待進一步研究。■

［1］李一兵，吳海訓，任大孟.抗反輻射導彈雷達誘餌合成場技術的研究［J］.信息技術，2003，27（12）：75-76.

［2］周偉光，羅積潤，王華彬.多輻射源合成場對反輻射導彈的誘偏作用［J］.電子學報，2008，36（6）：1193-1197.

［3］司錫才，趙建民.寬頻帶反輻射導彈導引頭技術基礎［M］.哈爾濱：哈爾濱工程大學出版社，1996.

［4］肖本龍，楊黎都，張程.兩點源誘偏輻射式仿真試驗誘餌設置方法［J］.現代電子技術，2012，35（1）：4-7.

［5］高彬，郭慶豐，呂善偉.有源誘偏抗反輻射導彈技術研究［J］.現代雷達，2006，28（10）：12-15.

［6］王華彬，周偉光，羅積潤.雷達抗反輻射導彈誘餌布陣仿真研究［J］.現代雷達，2009，31（7）：17-21.

［7］Li X，Yuan ZW，Yang B.Design of anti-radar missile decoy system arrange project and decoying effect analysis［J］.Systems and Electronics，2005，27（3）：439-445.

［8］Li YM，Gan DY，Su DL.Analysis of amplitude for the antiradiation weapon antagonizing active decoy［C］∥8th International Symposium on Antennas，Propagation and EM Theory.Kunming，China：IEEE，2008：1198-1202.