演化博弈的元胞自動機仿真

(西北民族大學，甘肅 蘭州 730124)

隨著互聯網的發展，網絡媒體被公認為是繼報紙、廣播、電視之后的“第四媒體”。現代社會，上網瀏覽網頁、查看新聞、關注政治、發表言論的網民越來越多，網絡以其自由、開放的特性吸引著更多人的關注和青睞。網絡論壇(BBS)、網絡聊天室(Chat Room)、個人博客(BLOG)、維基(Wiki)等等，一系列傳播工具的出現就使得網絡輿情的傳播方式和渠道呈現出多元化趨勢[1]。與一般社會輿情相比，網絡輿情具有虛擬性、平等性和開放性特點，是社會輿情的一個子集，網絡主體是網民，本體是網民的意志、傾向和愿望，具有社會輿情的共同特點。由于因特網的全球分布和即時傳送，其影響范圍和程度為傳統媒體遠不能及。輿情發展到高級階級會形成輿論，輿論是對某一特定事態的一種一致性的公開評價，是一種已經形成了的對事物態度傾向性統一觀點的表達，不管其主體是公眾或官方，都會對社會產生重大影響。

本文率先使用博弈理論對網絡輿情的傳播過程進行解析，并建立一個相應的博弈演化數學模型，利用MATLAB 編程，對模型進行計算機仿真。驗證了模型的合理性與可行性，對網絡輿論的引導和預警有一定的指導意義，有助于解決網絡安全問題。

1 博弈論概述

1.1 博弈論的基本概念

博弈論(game theory)，又名“決策論”、“賽局理論”。一場博弈需要有兩個以上的參與者，每個參與者都對他人的行動做出反應。博弈論是研究個體如何在錯綜復雜、相互影響的環境中做出最合理的反應[2]。一個簡單的博弈通常還有如下幾個要素組成[3]:

(1)參與者(players):或者稱為“比賽者”、“代理人”，在一場競賽或博弈中，參與者至少需要兩個，且每一個參與者都有決策權。

(2)策略(strategies):一局博弈中，每個參與者都有選擇實際可行的、完整的行動方案。該方案不是某階段的行動方案，而是指導整個行動的方案。

(3)收益(payoffs):每個參與者在一局博弈結束時的得失。收益不僅與該參與者自身所選擇的策略有關，還與所有參與者所選定的策略有關。

(4)納什均衡(Nash Equilibrium):均衡意味著每個參與者所采取的策略都是對其他參與者策略的最優反應。于是所有的參與者都面臨這樣一種情況，當其他參與者不改變策略時，他此時的策略是最好的。

1.2 囚徒困境博弈(prisoner’s dilemma game，PDG)

囚徒困境由數學家Albert Tucher:于1950年提出[4]，模型中假設兩個小偷聯合作案后被捕，但警察沒有足夠的證據，因此警察設計了一個機制，將他們關在不同的屋子里分別訊問如果雙方都保持沉默(與對方合作)，則兩人都會因證據不足而被輕判(雙方收益均為R);如果一方承認(背叛對方)而另一方保持沉默，則承認者將無罪釋放(收益為T)，保持沉默的一方將被重判(收益為S);如果雙方都背叛對方而選擇招供，則雙方都會被判刑(雙方收益均為P)在PDG 中，收益參數需滿足T ＞R ＞P ＞S，且2R ＞T+S 收益矩陣可以表示為表一。

2 模型的建立

利用元胞自動機的研究方法，首先將網絡空間抽象成一個二維平面，將這個平面平均分割為n ×n個方格[5]。圖1即為一個7 ×7的方格平面，每個方格稱之為一個元胞，代表網絡空間的一個個體。針對n ×n的二維元胞空間里任一元胞可采用形如(i，j)的數對來確定，其中2≤(i，j)≤n-1，則其鄰居可表示為:(i，j-1)，(i，j+1)，(i+1，j)，(i+1，j+1)，(i+1，j-1)，(i-1，j-1)，(i-1，j)，(i-1，j+1)。

圖1 二維元胞自動機的鄰居模型

每一個元胞代表著一個個體，任意選取一個元胞(i，j)作為中心元胞，確定其為研究對象，即中心元胞發表一種言論或態度，將會與周圍鄰居元胞進行博弈[6]，對自身以及鄰居元胞產生一定影響，采用一個2 ×2的矩陣來表示中心元胞與任一鄰居元胞博弈的結果。

中心元胞與其右方鄰居元胞博弈可產生如下矩陣:

表2 中心元胞與其右方鄰居元胞博弈收益

其中:

E11(i，j)表示中心元胞(i，j)和(i，j+1)在對某一輿情都持贊成態度時，元胞第一次博弈后中心元胞(i，j)的博弈收益;E12(i，j)表示中心元胞(i，j)在對某一輿情持支持態度，(i，j+1)持反對態度時，元胞第一次博弈后中心元胞(i，j)的博弈收益;

E11(i，j+1)則表示中心元胞(i，j)和(i，j+1)在對某一輿情都持贊成態度時，元胞第一次博弈后，元胞(i，j+1)的博弈收益;E12(i，j+1)表示中心元胞(i，j)在對某一輿情持支持態度，(i，j+1)持反對態度時，元胞第一次博弈后元胞(i，j+1)的博弈收益;

E21(i，j)表示中心元胞(i，j)在對某一輿情持反對態度，(i，j+1)持支持態度時，元胞第一次博弈后元胞(i，j)博弈收益;E22(i，j)表示二者皆持反對態度時，元胞第一次博弈后中心元胞(i，j)的收益;

E21(i，j+1)則表示中心元胞(i，j)在對某一輿情持反對態度，(i，j+1)持支持態度時，元胞第一次博弈后(i，j+1)的收益;E22(i，j+1)表示二者皆持反對態度時，元胞第一次博弈后中心元胞(i，j+1)的收益;

當元胞(i，j)分別與鄰居元胞進行一次博弈之后，根據每次博弈收益計算出此次博弈中心元胞(i，j)平均收益W(i，j)即為:

當元胞、鄰居元胞都博弈一次后，就可以得到此次博弈之后每個元胞的平均收益，并由此計算出中心元胞加8 鄰居的總平均收益:

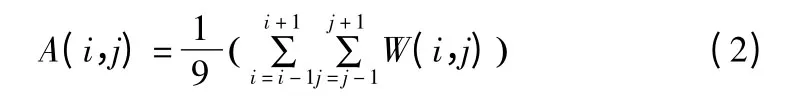
并以此與W(i，j)作比較，作為元胞下一個時段狀態值改變的主要依據。

在上述條件下，假設參與博弈的個體中贊成者比例為ρ，而反對者所占的比例為1-ρ，則贊成者的收益PC可以表示為:

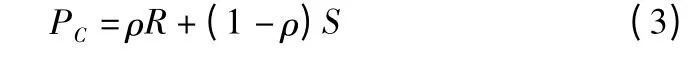
反對者的收益PD可以表示為:

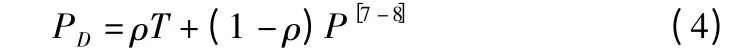
以囚徒困境為例，按照Nowak 和May所使用的博弈參數R=1，T=b(1 ＜b ＜2)，P=S=0[9]代入上式。

3 模型演化規則

1)假設元胞(i，j)初始賦值即為t=0 時刻此元胞的收益值;

2)元胞(i，j)以初始狀態值分別與所有鄰居元胞進行博弈，每一次博弈都有一個收益，然后對所有收益的和求平均，即為W(i，j);

3)按以上規則，平面空間內所有元胞都與自己的鄰居元胞進行一次博弈，分別求出每個元胞的平均收益，并以此計算整個平面內所有元胞的總平均收益A(n，n);

4)把W(i，j)與A(n，n)分別做比較，當以W(i，j)≥A(n，n)元胞(i，j)在下一時刻改變其狀態，否則不改變;

5)將上時刻元胞的平均收益記為下時刻元胞的初始值，按2)、3)、4)進行下一步演化。

4 模型仿真結果與分析

根據上述理論，借助MATLAB 軟件進行計算機模擬仿真，多次仿真比較后發現隨著系統演進的繼續，個體之間發生交互作用，觀點開始發生改變，圖3為每仿真五次得到的狀態圖，包括初始狀態、演化中的兩個狀態和最終狀態[10-11]。(藍色表示該元胞持支持態度，黃色表示持反對態度)

圖2 博弈演化過程

由上圖可以看出，在觀點均勻分布的初始狀態下，隨著元胞間博弈和時間的影響，系統中網民輿情態度的發展有少量元胞呈現出群聚的現象。但在博弈演化過程中，輿情的傳播著很難發生大規模集群現象。

另一方面如統計圖3所示，網民對某一網絡輿情態度的發展變化態度最終趨于穩定的狀態。

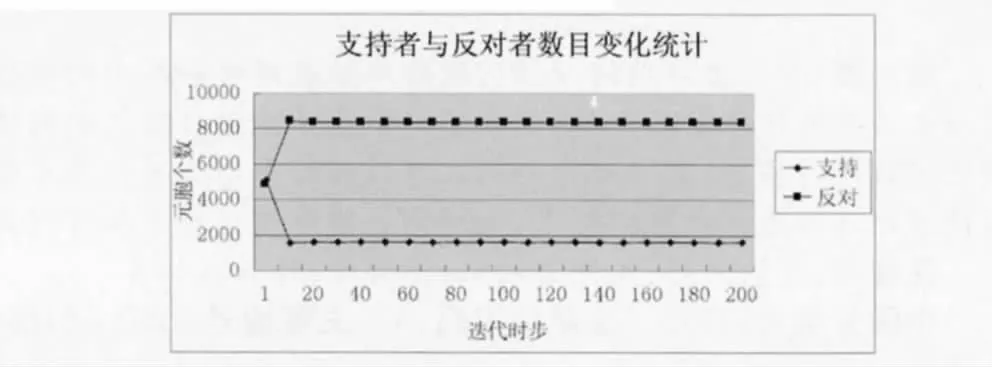
圖3 贊成者與反對者數量變化統計圖

5 結語

本文針對網絡輿情的傳播問題，建立數學模型，用博弈的相關理論對輿情傳播進行了剖析。在無引導策略的前提下，持贊成、反對的兩種態度在一定區域內均勻分布，利用MATLAB 算法模擬了輿情的自然演進過程。但是模型在上述假設的情況下建立，沒有考慮時間、元胞鄰居、媒體[6]等主要因素的影響，而在現實社會中，網絡輿論傳播是一個復雜系統，影響它的機制和因素有很多，考慮到個體差異、社會突發事件等諸多因素建立的模型將更加貼近現實、更加有效地模擬網絡輿論的傳播，因此本模型的普適性有一定的限制。

實際問題中，人員移動[12]、輿論潛伏期等均會影響輿論的發展，所以考慮這些因素，對模型進行改進，確定較為合理的匹配參數。

[1]劉毅，網絡輿情研究概論[M].天津:天津人民出版社.2007.(7)

[2]Von Neumann J，Morgenstern O.Theory of games and economic behavior[M]，Princeton，NJ:Princeton University Press，1953.

[3]Szabó G，Fáth G.Evolutionary games on graphs[J].Phys.Rep，2007，446:97-216.

[4]Rapoport A，Chammah A M，Prisoners Dilemma，Ann Arbor，MI:University of Michigan Press，1965.

[5]代瓊琳，復雜網絡上的演化博弈動力學研究[D].北京:北京郵電大學，2011.

[6]BERT INO E，SANDHU R.Database security-concepts，app roa2ches，and challenges [J]IEEE Transaction son Dependable and Secure Computing，2005，2(1):2-19.

[7]Hofbauer J，Sigmund K，Evolutionary Games and Population Dynamies，Cambridge:Cambridge University Press，1998.

[8]Hauert C，Szab G，Game theory and Physies，Am.J.Phys.73，2005，405-414

[9]Nowak M A，May R，Evolultionary games and spatial chaos，Nature 359，1992，826-829.

[10]劉建明，輿論傳播，北京:清華大學出版社，2001年

[11]張立，網絡輿論傳播中若干算法的研究，104～110，2009年6月

[12]李蘭瑛.基于CA的網絡輿論傳播因素的研究[J].科學技術與工程，2008，8(22):6179-6186.